一、说明
马哈拉诺比斯距离(Mahalanobis Distance)是一种测量两个概率分布之间距离的方法。它是基于样本协方差矩阵的函数,用于评估两个向量之间的相似程度。Mahalanobis Distance考虑了数据集中各个特征之间的协方差,因此比欧氏距离更适合用于涉及多个特征的数据集。Mahalanobis Distance可以应用于各种机器学习算法中,如聚类分析、分类算法和异常检测。
维沙尔·夏尔马
二、基本概念介绍
马氏距离是一种统计工具,用于测量点和分布之间的距离。它是一种强大的技术,可考虑数据集中变量之间的相关性,使其成为各种应用(如异常值检测、聚类和分类)中的宝贵工具。
例如,让我们考虑一个场景,其中一家公司想要识别信用卡交易中的潜在欺诈行为。该公司收集有关各种变量的数据,例如交易金额,位置,时间和其他信用卡交易详细信息。然后,它使用马氏距离来测量每笔交易与所有交易分布之间的距离。通过这样做,它可以识别与其他交易明显不同的交易,并可能表明欺诈活动。
马氏距离测量点和分布之间的距离,考虑数据中变量之间的相关性。它是点 x 与具有平均向量 μ 和协方差矩阵 Σ 的分布之间的距离。马氏距离的公式如下:
D² = (x-μ)TΣ⁻¹(x-μ)
其中 D² 是平方马氏距离,x 是相关点,μ 是分布的平均向量,Σ 是分布的协方差矩阵,T 表示矩阵的转置。
为了更好地理解这个公式,让我们举一个例子。假设我们有一个包含两个变量 X 和 Y 的数据集,并且我们想要测量一个点 (2, 3) 与数据集中所有点的分布之间的距离。我们计算数据集的平均向量和协方差矩阵如下:
μ = [mean(X), mean(Y)] = [3, 4]
Σ = [[var(X), cov(X,Y)], [cov(X,Y), var(Y)]] = [[2, -1], [-1, 2]]
现在,我们可以使用马氏距离公式来计算点 (2, 3) 和分布之间的距离:
D² = ([2, 3]-[3, 4])T[[2, -1], [-1, 2]]⁻¹([2, 3]-[3, 4])
= [-1, -1]T[[2, -1], [-1, 2]]⁻¹[-1, -1]
= [2, -2]T[[2/3, 1/3], [1/3, 2/3]][2, -2]
= [2/3, -2/3]T[2, -2]
= 4/3。
因此,点 (2, 3) 与分布之间的马氏距离平方为 4/3。通过计算马氏距离,我们可以确定点与分布的距离,考虑 X 和 Y 变量之间的相关性。
import numpy as np
from scipy.spatial.distance import mahalanobis
from sklearn.datasets import make_blobs
# Create a dataset with 2 clusters
X, y = make_blobs(n_samples=100, centers=2, random_state=42)
# Calculate the mean vector and covariance matrix of the dataset
mu = np.mean(X, axis=0)
sigma = np.cov(X.T)
# Calculate the Mahalanobis Distance between two points
x1 = [2, 2]
x2 = [-2, -2]
dist_x1 = mahalanobis(x1, mu, np.linalg.inv(sigma))
dist_x2 = mahalanobis(x2, mu, np.linalg.inv(sigma))
# Print the distances
print("Distance between point x1 and the distribution:", dist_x1)
print("Distance between point x2 and the distribution:", dist_x2)
#OUTPUT
Distance between point x1 and the distribution: 2.099478227196236
Distance between point x2 and the distribution: 8.065203145117373以下是如何使用马氏距离的一些示例:
- 异常值检测:马氏距离可以检测数据集中的异常值。异常值是与数据集其余部分明显不同的数据点。通过计算每个数据点与数据集平均值之间的马氏距离,我们可以识别远离平均值的数据点。这些数据点可被视为异常值,可能需要删除或进一步调查。
- 聚类:马氏距离也可用于聚类数据点。聚类是将相似的数据点分组在一起的过程。通过计算每个数据点之间的马氏距离和每个聚类的平均值,我们可以确定数据点属于哪个聚类。此方法可用于对具有不同方差或协方差的数据点进行聚类分析。
- 图像分类: 马氏距离可用于图像分类任务。此应用程序使用马氏距离来测量测试图像和一组训练图像之间的相似性。通过计算测试图像和每个训练图像之间的马氏距离,我们可以确定哪个训练图像与测试图像最相似。此方法对于人脸识别和对象检测等任务很有用。
- 欺诈检测:马氏距离可用于金融交易中的欺诈检测。通过计算一笔交易和一组历史交易之间的马氏距离,我们可以确定该交易是不寻常的还是可疑的。此方法可用于检测可能被忽视的欺诈易
以下是如何使用马氏距离的一些示例:
三、示例
下面是如何使用马哈拉诺比斯距离为现实生活中的数据集创建美丽图的示例:
在本例中,让我们使用著名的鸢尾花数据集,其中包含 150 朵鸢尾花的测量值。我们将使用萼片长度、宽度和花瓣长度作为我们的特征。
首先,我们将计算数据集中每个数据点的马氏距离。我们可以在 Python 中使用以下代码来做到这一点:
import numpy as np
from scipy.spatial.distance import mahalanobis
# load the iris dataset
from sklearn.datasets import load_iris
iris = load_iris()
# calculate the mean and covariance matrix of the dataset
mean = np.mean(iris.data, axis=0)
cov = np.cov(iris.data.T)
# calculate the Mahalanobis distance for each data point
mahalanobis_dist = [mahalanobis(x, mean, np.linalg.inv(cov)) for x in iris.data]接下来,我们可以使用前两个特征(萼片长度和萼片宽度)创建虹膜数据集的散点图,并根据其马氏距离为每个数据点着色。我们可以使用颜色图将马氏距离映射到色标。这是该图的代码:
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
# create a color map for the Mahalanobis distances
cmap = ListedColormap(['r', 'g', 'b'])
norm = plt.Normalize(min(mahalanobis_dist), max(mahalanobis_dist))
# create a scatter plot of the iris dataset
plt.scatter(iris.data[:, 0], iris.data[:, 1], c=mahalanobis_dist, cmap=cmap, norm=norm)
# add a color bar
plt.colorbar()
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.title('Mahalanobis Distance for Iris Dataset')
plt.show()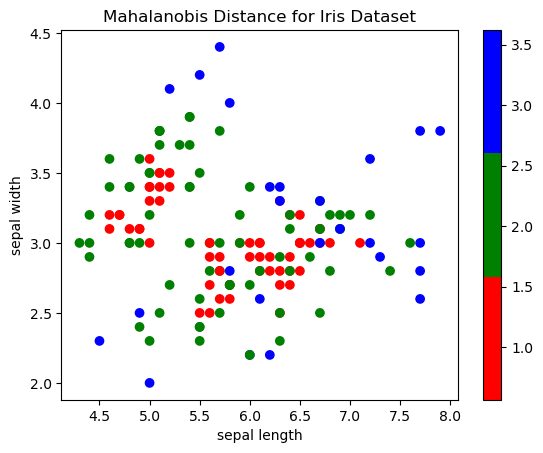
生成的图显示了鸢尾花数据集,每个数据点根据其马氏距离着色。远离平均值的数据点(即异常值)以红色显示,而接近平均值的数据点以绿色和蓝色着色。
下面是另一个使用sci-kit-learn库附带的著名Wine数据集的示例:
import numpy as np
from scipy.spatial.distance import mahalanobis
import pandas as pd
from sklearn.datasets import load_wine
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
# load the wine dataset
wine = load_wine()
wine_df = pd.DataFrame(wine.data, columns=wine.feature_names)
# calculate the mean and covariance matrix of the dataset
mean = np.mean(wine_df, axis=0)
cov = np.cov(wine_df.T)
# calculate the Mahalanobis distance for each data point
mahalanobis_dist = [mahalanobis(x, mean, np.linalg.inv(cov)) for x in wine_df.values]
# create a scatter plot of the wine dataset using two highly correlated features
plt.scatter(wine_df['flavanoids'], wine_df['color_intensity'], c=mahalanobis_dist, cmap='coolwarm')
# add a color bar
plt.colorbar()
plt.xlabel('flavanoids')
plt.ylabel('color_intensity')
plt.title('Mahalanobis Distance for Wine Dataset')
plt.show()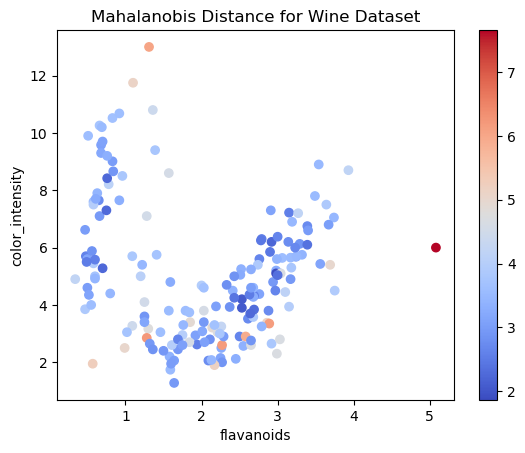
两个高度相关的特征(类黄酮和color_intensity)的散点图,每个数据点根据其马氏距离着色。
![linux鲁班猫代码初尝试[编译镜像][修改根文件系统重编译][修改设备树改屏幕为MIPI]](https://img-blog.csdnimg.cn/625fa74898f84a52b8366e8cd4e00f6b.png)