使用稀疏矩阵存储包含众多零值元素的数据,可以节省大量内存并加快该数据的处理速度。sparse 是一种属性,可以将该属性分配给由
double
或
logical 元素组成的任何二维 MATLAB 矩阵。通过
sparse
属性,MATLAB 可以:
• 仅存储矩阵中的非零元素及其索引。
• 不必对零元素执行运算,从而减少计算时间。
对于满矩阵,MATLAB 将在内部存储每个矩阵元素。零值元素与任何其他矩阵元素需要的存储空间量相同。但是,对于稀疏矩阵,MATLAB 只会存储非零元素及其索引。对于零值元素百分比很高的大型矩阵,此方案可以极大地减少存储数据所需的内存量。whos
命令提供有关矩阵存储的高级信息,包括大小和存储类。例如,以下的
whos 列表显示了有关同一矩阵的稀疏版本和完全版本的信息。
M_full = magic(1100);
% Create 1100-by-1100 matrix.
M_full(M_full > 50) = 0;
% Set elements >50 to zero.
M_sparse = sparse(M_full);
% Create sparse matrix of same.
whos
Name Size Bytes Class Attributes
M_full 1100x1100 9680000 double
M_sparse 1100x1100 9608 double sparse
请注意,稀疏矩阵中使用的字节数较少,因为零值元素未被存储。
在计算效率方面,稀疏矩阵也具有显著的优点。与满矩阵的运算不同,稀疏矩阵的运算不会执行不必要的低级算术操作,例如加零(
x+0
始终为
x
)。这样便可大大缩短处理大量稀疏数据的程序的执行时间。
1.创建稀疏矩阵
MATLAB 从不会自动创建稀疏矩阵。相反,还必须确定矩阵中是否包含足够高百分比的零元素,以便利用稀疏方法。
矩阵的密度是指非零元素数目除以矩阵元素总数。对于矩阵 M
,这将为
nnz(M) / prod(size(M));
或
nnz(M) / numel(M);
密度非常低的矩阵通常很适合使用稀疏格式。
1.1将满矩阵转换为稀疏矩阵
可以使用带有单个参数的 sparse 函数将满矩阵转换为稀疏存储。例如:
A = [ 0 0 0 5
0 2 0 0
1 3 0 0
0 0 4 0];
S = sparse(A)
S =
(3,1) 1
(2,2) 2
(3,2) 3
(4,3) 4
(1,4) 5
列显输出中列出了 S 的非零元素及其行索引和列索引。这些元素按列排序,反映了内部数据结构体。如果矩阵阶数不太高,可以使用
full
函数将稀疏矩阵转换为满存储。例如,
A = full(S) 可反向转换该示例。
将满矩阵转换为稀疏存储并非生成稀疏矩阵的最常用方法。如果矩阵的阶数足够低可以进行满存储,则转换为稀疏存储很难显著节省内存。
1.2直接创建稀疏矩阵
可以使用带有五个参数的 sparse
函数,基于一列非零元素来创建稀疏矩阵。
S = sparse(i,j,s,m,n)
i 和
j
分别是矩阵中非零元素的行索引和列索引的向量。
s
是由对应的
(i,j)
对指定索引的非零值的向量。
m
是生成的矩阵的行维度,
n 是其列维度。前一示例中的矩阵
S
可以直接通过以下表达式生成
S = sparse([3 2 3 4 1],[1 2 2 3 4],[1 2 3 4 5],4,4)
S =
(3,1) 1
(2,2) 2
(3,2) 3
(4,3) 4
(1,4) 5
sparse 命令具有许多备用形式。上面示例使用的形式将矩阵中的最大非零元素数设置为 length(s)。如果需要,可以追加第六个参数用来指定更大的最大数,这样能在以后添加非零元素,而不必重新分配稀疏矩阵。
二阶微分算子的矩阵表示形式就是一个很好的稀疏矩阵示例。它是一个三对角矩阵,其中 -2s 在对角线上,1s 在上对角线和下对角线上。有多种方式生成此类炬阵,这里只是一种可能性。
n = 5;
D = sparse(1:n,1:n,-2*ones(1,n),n,n);
E = sparse(2:n,1:n-1,ones(1,n-1),n,n);
S = E+D+E'
S =
(1,1) -2
(2,1) 1
(1,2) 1
(2,2) -2
(3,2) 1
(2,3) 1
(3,3) -2
(4,3) 1
(3,4) 1
(4,4) -2
(5,4) 1
(4,5) 1
(5,5) -2
现在,F = full(S)
显示相应的满矩阵。
F = full(S)
F =
-2 1 0 0 0
1 -2 1 0 0
0 1 -2 1 0
0 0 1 -2 1
0 0 0 1 -2
1.3基于稀疏矩阵的对角线元素创建稀疏矩阵
基于稀疏矩阵的对角线元素创建稀疏矩阵是一种常用操作,因此函数 spdiags 可以处理此任务。其语法是
S = spdiags(B,d,m,n)
要创建大小为 m×n 且元素在 p
对角线上的输出矩阵
S
:
• B
是大小为
min(m,n)
×p 的矩阵。
B
的列是用于填充
S
对角线的值。
• d
是长度
p
的向量,其整数元素可以指定要填充的
S
对角线。
即,B
的列
j
中的元素填充
d
的元素
j
指定的对角线。
注意 如果
B
的列长度超过所替换的对角线,则上对角线从
B
列的下部获取,下对角线从 B 列的上部获取。例如,考虑使用矩阵
B
和向量
d
。
B = [ 41 11 0
52 22 0
63 33 13
74 44 24 ];
d = [-3
0
2];
使用这些矩阵创建 7×4 稀疏矩阵 A
:
A = spdiags(B,d,7,4)
A =
(1,1) 11
(4,1) 41
(2,2) 22
(5,2) 52
(1,3) 13
(3,3) 33
(6,3) 63
(2,4) 24
(4,4) 44
(7,4) 74
在其满矩阵形式中,A
类似于:
full(A)
ans =
11 0 13 0
0 22 0 24
0 0 33 0
41 0 0 44
0 52 0 0
0 0 63 0
0 0 0 74
spdiags 还可以从稀疏矩阵中提取对角线元素,或将矩阵对角线元素替换为新值。键入
help spdiags 以了解详细信息。
1.4导入稀疏矩阵
可以在 MATLAB 环境外部通过计算导入稀疏矩阵。结合使用 spconvert
函数与
load 命令导入包含索引和非零元素列表的文本文件。例如,考虑使用三列文本文件
T.dat,它的第一列是行索引列表,第二列是列索引列表,第三列是非零值列表。这些语句将
T.dat
加载到 MATLAB 中并将其转换为稀疏矩阵
S
:
load
T.dat
S = spconvert(T)
save 和
load
命令还可以处理作为 MAT 文件中的二进制数据存储的稀疏矩阵。
2.访问稀疏矩阵
2.1非零元素
以下多条命令可以提供有关稀疏矩阵的非零元素的概要信息:
• nnz
返回稀疏矩阵中的非零元素数。
• nonzeros
返回包含稀疏矩阵的所有非零元素的列向量。
• nzmax
返回为稀疏矩阵的非零项分配的存储空间量。
要尝试上述中的一些命令,请加载提供的稀疏矩阵 west0479
,该矩阵是 Harwell-Boeing 集合之一。
load
west0479
whos
Name Size Bytes Class Attributes
west0479 479x479 34032 double sparse
该矩阵为八个阶段的化工精馏塔建模。尝试以下命令。
nnz(west0479)
ans =
1887
format
short e
west0479
west0479 =
(25,1) 1.0000e+00
(31,1) -3.7648e-02
(87,1) -3.4424e-01
(26,2) 1.0000e+00
(31,2) -2.4523e-02
(88,2) -3.7371e-01
(27,3) 1.0000e+00
(31,3) -3.6613e-02
(89,3) -8.3694e-01
(28,4) 1.3000e+02
nonzeros(west0479)
ans =
1.0000e+00
-3.7648e-02
-3.4424e-01
1.0000e+00
-2.4523e-02
-3.7371e-01
1.0000e+00
-3.6613e-02
-8.3694e-01
1.3000e+02
.
注意 使用
Ctrl+C
随时停止列出
nonzeros
。
请注意,最初在默认情况下,nnz
与 nzmax 的值相同。即,非零元素数等于为非零元素分配的存储位置数。但是,如果将其他的数组元素置零,MATLAB 不会动态释放内存。将某些矩阵元素的值更改为零时会更改
nnz
的值,但不会更改
nzmax 的值。但是,可以根据需要将尽可能多的非零元素添加到矩阵中。不受 nzmax
原始值的限制。
2.2索引和值
对于任何矩阵,无论是满矩阵还是稀疏矩阵,find
函数都会返回非零元素的索引和值。其语法是
[i,j,s] = find(S);
find 返回向量
i
中的非零值的行索引、向量
j
中的列索引以及向量
s 中的自身非零值。下面的示例使用find
查找稀疏矩阵中的非零索引和值。
sparse
函数同时使用
find
输出和矩阵大小重新创建矩阵。
S1 = west0479;
[i,j,s] = find(S1);
[m,n] = size(S1);
S2 = sparse(i,j,s,m,n);
2.3稀疏矩阵运算中的索引
由于稀疏矩阵是以压缩稀疏列格式存储的,因此为稀疏矩阵进行索引的相关成本与为满矩阵进行索引的相关成本不同。在只需更改稀疏矩阵中的若干元素时,这类成本可忽略不计,因此,在这类情况下,通常使用常规数组索引来重新分配值:
B = speye(4);
[i,j,s] = find(B);
[i,j,s]
ans =
1 1 1
2 2 1
3 3 1
4 4 1
B(3,1) = 42;
[i,j,s] = find(B);
[i,j,s]
ans =
1 1 1
3 1 42
2 2 1
3 3 1
4 4 1
在存储新矩阵时,为使 42
位于
(3,1) 位置,MATLAB 会在非零值向量和下标向量中插入额外的一行,然后移动
(3,1) 后面的所有矩阵值。如果线性索引超过
2^48-1(即当前矩阵中允许的元素数上限),使用线性索引在大型稀疏矩阵中访问或指定元素将失败。
S = spalloc(2^30,2^30,2);
S(end) = 1
Maximum variable size allowed by the program is exceeded.
要访问其线性索引大于 intmax
的元素,请使用数组索引:
S(2^30,2^30) = 1
S =
(1073741824,1073741824) 1
尽管在稀疏矩阵中进行索引以更改单个元素的成本可忽略不计,但该成本在循环环境下会增加,而且在大型矩阵中该操作可能会使执行速度变得很慢。因此,在需要更改大量稀疏矩阵元素的情况下,最好使用向量化方法而不要使用循环方法来执行该操作。例如,考虑稀疏单位矩阵:
n = 10000;
A = 4*speye(n);
以循环方式更改 A
的元素慢于类似的向量化运算:
tic
A(1:n-1,n) = -1;
A(n,1:n-1) = -1;
toc
Elapsed time is 0.003344 seconds.
tic
for
k = 1:n-1
C(k,n) = -1;
C(n,k) = -1;
end
toc
Elapsed time is 0.448069 seconds.
由于 MATLAB 以压缩稀疏列格式存储稀疏矩阵,因此,在循环的每个遍历期间,它都需要移动 A 中的多个条目。如果为稀疏矩阵预分配内存,然后以类似的逐个元素的方式填充,会使对稀疏数组进行索引产生大量开销:
S1 = spalloc(1000,1000,100000);
tic;
for
n = 1:100000
i = ceil(1000*rand(1,1));
j = ceil(1000*rand(1,1));
S1(i,j) = rand(1,1);
end
toc
Elapsed time is 2.577527 seconds.
构建索引和值向量则无需为稀疏数组进行索引,因此这种方法的速度快得多:
i = ceil(1000*rand(100000,1));
j = ceil(1000*rand(100000,1));
v = zeros(size(i));
for
n = 1:100000
v(n) = rand(1,1);
end
tic;
S2 = sparse(i,j,v,1000,1000);
toc
Elapsed time is 0.017676 seconds.
因此,最好使用构造函数(例如 sparse
或
spdiags 函数)一次构造所有稀疏矩阵。例如,假定需要稀疏形式的坐标矩阵
C
:
4 0 0 0 −1
0 4 0 0 −1
C = 0 0 4 0 −1
0 0 0 4 −1
1 1 1 1 4
使用 sparse
函数,以及行下标、列下标和值组成的三联对组,直接构造该五列矩阵:
i = [1 5 2 5 3 5 4 5 1 2 3 4 5]';
j = [1 1 2 2 3 3 4 4 5 5 5 5 5]';
s = [4 1 4 1 4 1 4 1 -1 -1 -1 -1 4]';
C = sparse(i,j,s)
C =
(1,1) 4
(5,1) 1
(2,2) 4
(5,2) 1
(3,3) 4
(5,3) 1
(4,4) 4
(5,4) 1
(1,5) -1
(2,5) -1
(3,5) -1
(4,5) -1
(5,5) 4
输出中值的顺序反映了底层的按列存储。
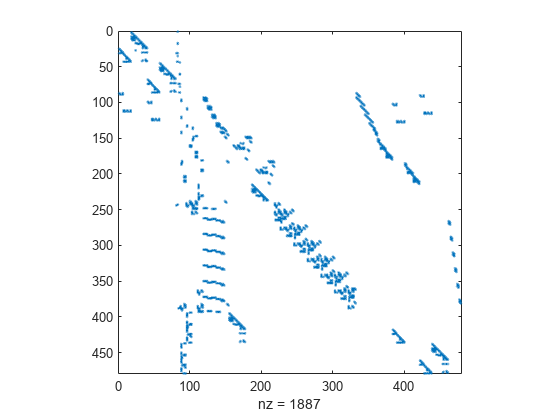
2.4可视化稀疏矩阵
以图的形式查看非零元素在稀疏矩阵内的分布通常很有用。MATLAB spy 函数生成稀疏结构的模板视图,其中图表中的每点代表一个非零数组元素的位置。例如:加载提供的稀疏矩阵
west0479
,该矩阵是 Harwell-Boeing 集合之一。
load
west0479
查看稀疏结构体。
spy(west0479)








![[GAN] 使用GAN网络进行图片生成的“调参人”入门指南——生成向日葵图片](https://img-blog.csdnimg.cn/5e6eb9c0031a429781f5aaad1d10a86e.gif#pic_center)