概述

在公司项目中使用到 wkhtmltopdf 转换PDF，由于 wkhtmltox-0.12.5 版本 echarts 图形虚线样式，需要升级 wkhtmltox-0.12.6 版本来解决。

官网地址

wkhtmltopdf ：https://wkhtmltopdf.org/

windows 安装

下载流程及安装流程

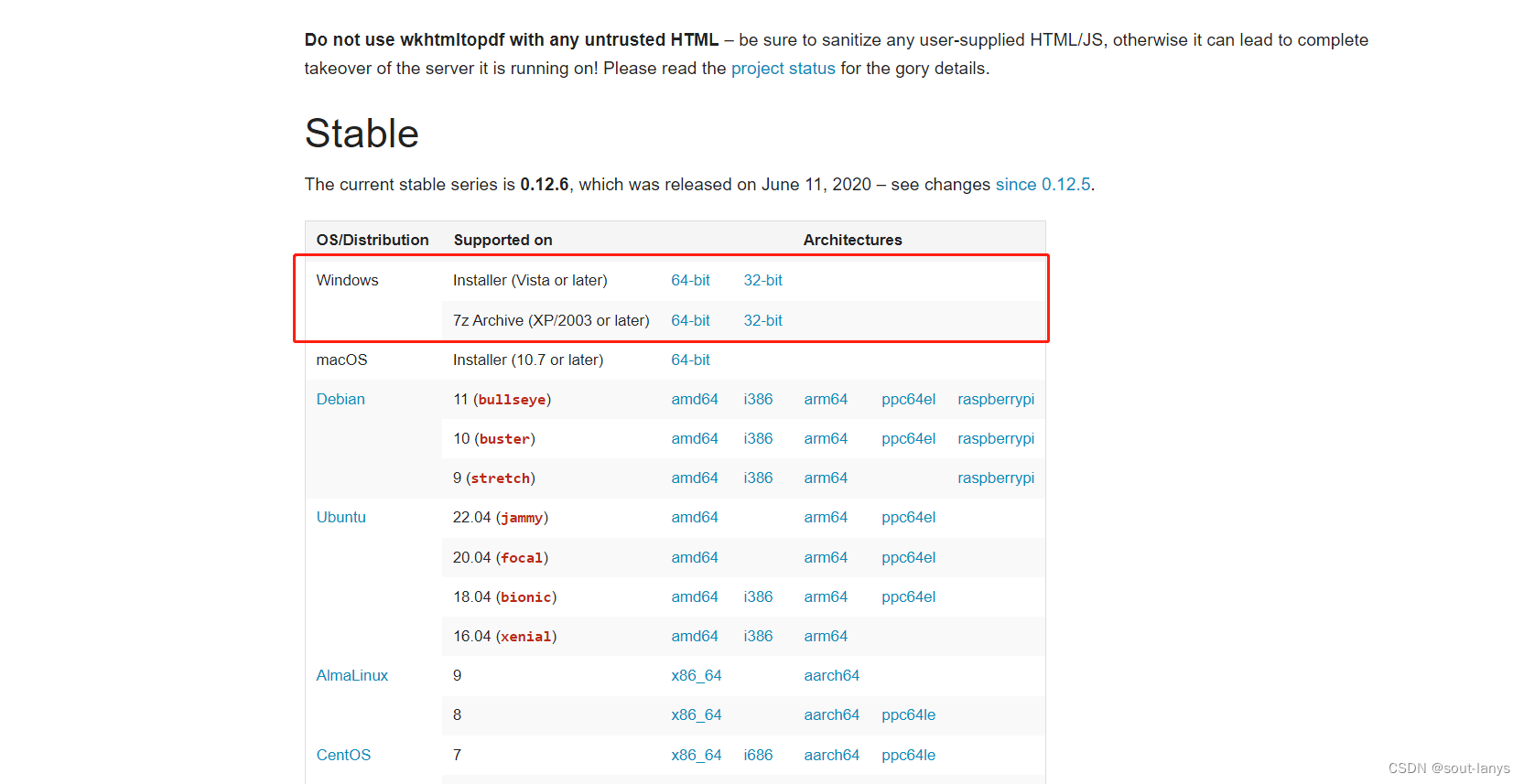
1. 进入官网：https://wkhtmltopdf.org/
2. 点击右上角 Downloads
3. 选择 windows 版本下载，我选择第一个 Installer… 64-bit
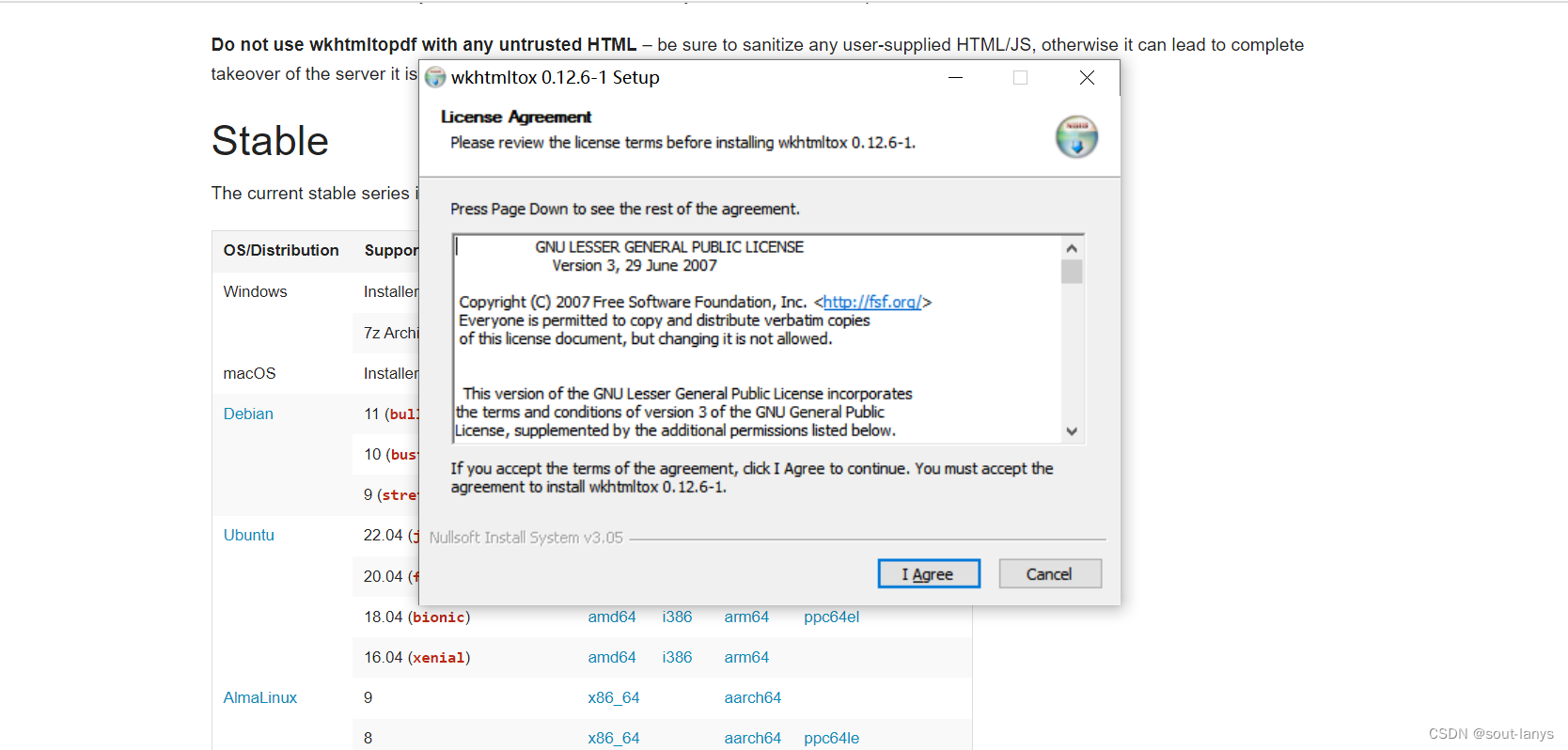
4. 下载完成后一直 next 就行

查看安装版本

# 查看安装版本
wkhtmltopdf -V

PDF转换测试

模版：

1. wkhtmltopdf 页面路径 转换文件名称
2. wkhtmltopdf 页面路径 /目录/转换文件名称

截图操作流程

Linux 安装

前提

如果之前有安装老版本的话需要先卸载

# 先查询安装的软件（此处为包含wkhtml）
rpm -qa |grep wkhtml  

# 卸载对应软件
rpm -e 软件名称

# 例如
rpm -e wkhtmltox-0.12.6-1.centos8.x86_64

安装流程

• 下载方式：官网下载、liunx中下载

# liunx下载 版本：centos7 wkhtmltox-0.12.6-1 版本
wget  https://github.com/wkhtmltopdf/packaging/releases/download/0.12.6-1/wkhtmltox-0.12.6-1.centos7.x86_64.rpm

# liunx下载 版本：centos8 wkhtmltox-0.12.6-1 版本
wget  https://github.com/wkhtmltopdf/packaging/releases/download/0.12.6-1/wkhtmltox-0.12.6-1.centos8.x86_64.rpm

• rpm 安装：提供两个，具体根据自己服务器来

# 版本：centos7 wkhtmltox-0.12.6-1 版本
rpm -ivh wkhtmltox-0.12.6-1.centos7.x86_64.rpm 
# 版本：centos8 wkhtmltox-0.12.6-1 版本
rpm -ivh wkhtmltox-0.12.6-1.centos7.x86_64.rpm

• 查看版本

 wkhtmltopdf -V

测试和 Windows 一样，就不多说。

• wkhtmltopdf 安装后的目录位置

# wkhtmltopdf 、wkhtmltoimages
cd /usr/local/bin/

Spring Boot 整合使用，下篇文章再讲