栈和队列修炼指南

1. 栈

1. 1 概念及结构

栈：是一种特殊的线性表，其只允许在固定的一端进行插入和删除元素的操作。进行数据插入和删除操作的一端称为栈顶，另一端为栈底。
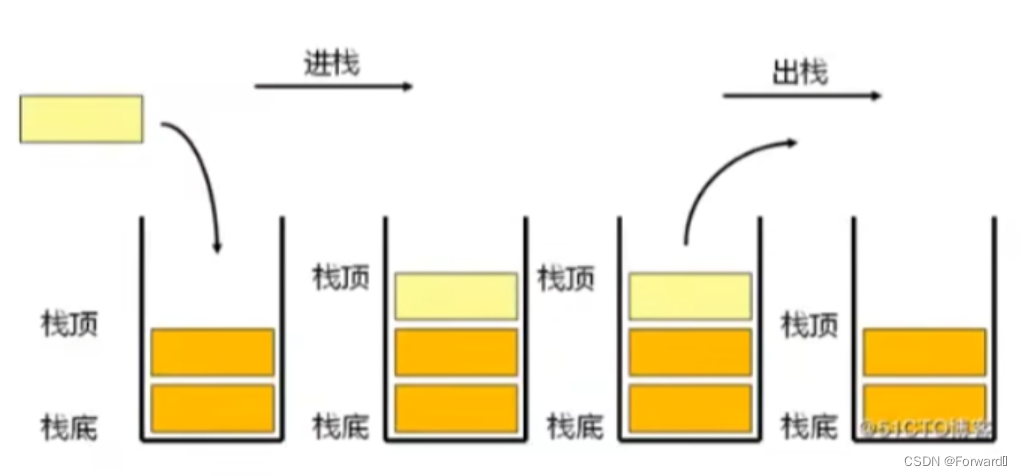
栈中的数据元素遵守后进先出原则(LIFO)原则
压栈：栈的插入操作称为进栈/压栈/入栈，其位置在栈顶
出栈：栈的删除操作称为出栈，其位置也在栈顶

1.2 分类（数组栈和链式栈）

数组栈（推荐方式，因为在数组尾插代价更小）

链式栈：相较数组栈无优势，且一般将链表尾作为栈底，链表头作为栈顶（单链表情况下）

1.3 数组栈

1.3.1 结构的定义

typedef int STElemType;
typedef struct Stack
{
	STElemType *data;	//动态栈
	int top;
	int capacity;
}ST;

1.3.2 初始化

void StackInit(ST *pt)
{
	pt->data = (SElemType *)malloc(N*sizeof(SElemTyp  e));
   	if (!pt->data)
   	{
   		perror("malloc");
   		exit(1);
	}
    
	pt->capacity = N;	//N表示初始的最大容量
	pt->top = 0;	//此时top指向的是栈顶元素的下一个位置，也可以定义为pt->top=-1,这样，top就是指向栈顶元素
}

1.3.3 销毁

void StackDestroy(ST *pt)
{
	free(pt->data);
	pt->top=pt->capacity=0;
}

1.3.4 判断栈是否为空

bool StackEmpty(ST *pt)
{
	return pt->top==0; 	//若为真即栈为空，则返回1，否则返回0
}

1.3.5入栈

void StackPush(ST *pt,SElemType x)
{
	if(pt->top==pt->capacity)			//如果容量已满
	{
		pt->capacity *= 2;		//将容量扩为原来的两倍
		ST* temp = realloc(pt->data, pt->capacity*sizeof(SElemType));
		if(!temp)
		{
			perror("malloc");
			exit(1);
		}
        
        pt->data = temp;
	}
    
    //入栈
	pt->data[pt->top]=x;
	pt->top++;
}

1.3.6 出栈

void StackPop(ST *pt) 
{
	assert(!stackEmpty(pt));	//栈不能为空
    
    //出栈
	pt->top--;
}

1.3.7 返回栈顶元素

SElemType StackTop(ST *pt)
{
	assert(!stackEmpty(pt));	//栈不能为空
    
	return pt->data[pt->top-1]; 
}

1.3.8 返回栈的元素个数

int StackSize(ST *pt)
{
	return pt->top;
}

1.3.9 将栈的元素全部取出

void StackPrint(ST *pt)
{
	assert(!stackEmpty(pt));	//栈不能为空
    
	while(!StackEmpty(pt))
	{
		printf("%d ",StackTop(pt));	//遵循先入后出原则，从上往下取
		pt->top--;
	}
}

1.4 练习

学习完栈的基本概念和相关操作后，你可以利用栈的特性做下面的OJ题：

有效括号序列👉题目解析

逆波兰表达式求值👉题目解析

删除字符串中的所有相邻重复项👉题目解析

包含min函数的栈👉题目解析

2. 队列

2.1 概念及结构

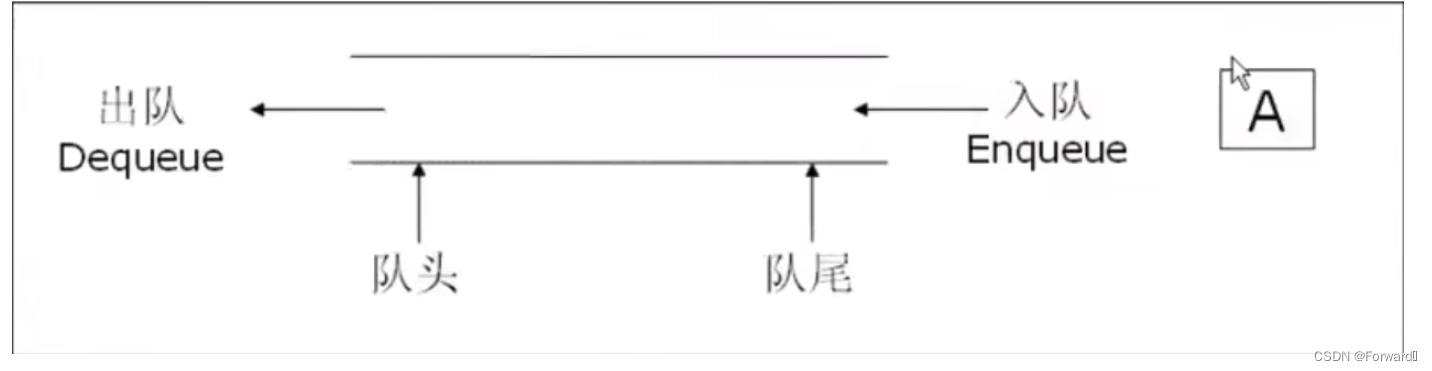
队列：只允许在一端进行入数据操作，在另一端进行删除数据操作的特殊线性表
遵循先进先出的原则FIFO
入队列：进行插入操作的一段叫做队尾
出队列：进行删除操作的一段叫做队头

2.2. 分类（数组队列和链队列）

数组队列：由于出队列出的是队头元素，因此数组队列出数据的效率低下，不推荐使用

链队列：入和出数据的效率都很高，是队列常用的表示法

2.3 链队列

2.3.1 结构的定义

typedef int QDataType;	//存储的数据类型

typedef struct QueueNode	//链队列的节点
{
	struct QueueNode *next;
	QDataType data;
}QueueNode;

typedef struct Queue	//定义存放指向队头，队尾指针的结构体
{
	QueueNode *head;	//指向队头
	QueueNode *tail;	//指向队尾
}Queue;

2.3.2 初始化

void QueueInit(Queue *pq)
{
	assert(pq);
	pq->head = NULL;
	pq->tail = NULL;
}

2.3.3 销毁

void QueueDestroy(Queue *pq)
{
	QueueNode *cur = pq->head;	//定义临时变量
	while (cur)
	{  
		pq->head = pq->head->next;	//链表下滑
		free(cur);		//释放空间
		cur = pq->head;	//更新临时变量
	} 
	pq->tail = NULL;	//空间释放完毕后head已经为空，但tail成为了野指针，所以要置空
}

2.3.4 判断队列是否为空

bool QueueEmpty(Queue *pq) 
{
	assert(pq);
    
	return pq->head == NULL;
}

2.3.4 入队

void QueuePush(Queue *pq,QDataType x)
{
	assert(pq);
    
	QueueNode *newnode=(QueueNode *)malloc(sizeof(QueueNode));		//创建新节点
    if (NULL == newNode)
    {
        perror("malloc");
        exit(1);
	}
	newnode->data=x;
	newnode->next=NULL;
    
	if(QueueEmpty(pq))	//如果队列为空
	{
		pq->head=newnode;	//使队头、队尾指针同时指向新节点
		pq->tail=newnode;
	}
	else
	{
		pq->tail->next=newnode;	//使队尾指针的指向下一个节点的指针指向新节点
		pq->tail=newnode;	//更新队尾指针
	}
}

2.3.5 出队

void QueuePop(Queue *pq) 
{
	assert(pq);
	assert(!QueueEmpty(pq));	//队列不能为空
    
	QueueNode *cur=pq->head;	//定义临时变量保存队头指针
	pq->head=pq->head->next;	//使队头指针指向下一个节点
	free(cur);		//释放原来的队头
    
	if(pq->head==NULL)
		pq->tail=NULL;	//如果节点已经全部出队，则要将队尾指针置空，防止形成野指针
}

2.3.6 返回队头/队尾数据域

//返回队头元素
QDataType QueueFront(Queue *pq)	 
{
	assert(pq);
	assert(!QueueEmpty(pq));
    
	return pq->head->data;
}

//返回队尾元素 
QDataType QueueBack(Queue *pq)
{
    assert(pq);
    assert(!QueueEmpty(pq));

    return pq->tail->data;
}

2.3.7 返回队列元素个数

int QueueSize(Queue *pq)
{
	QueueNode *cur=pq->head;
	int size=0;
    
	while(cur)
	{
		size++;
		cur=cur->next;
	}
    
	return size;
}
//也可以在队列结构体中增加size变量，每入队一个size就加一