28 玻尔兹曼机

28.1 模型定义

玻尔兹曼机是一张无向图，其中的隐节点和观测节点可以有任意连接如下图：

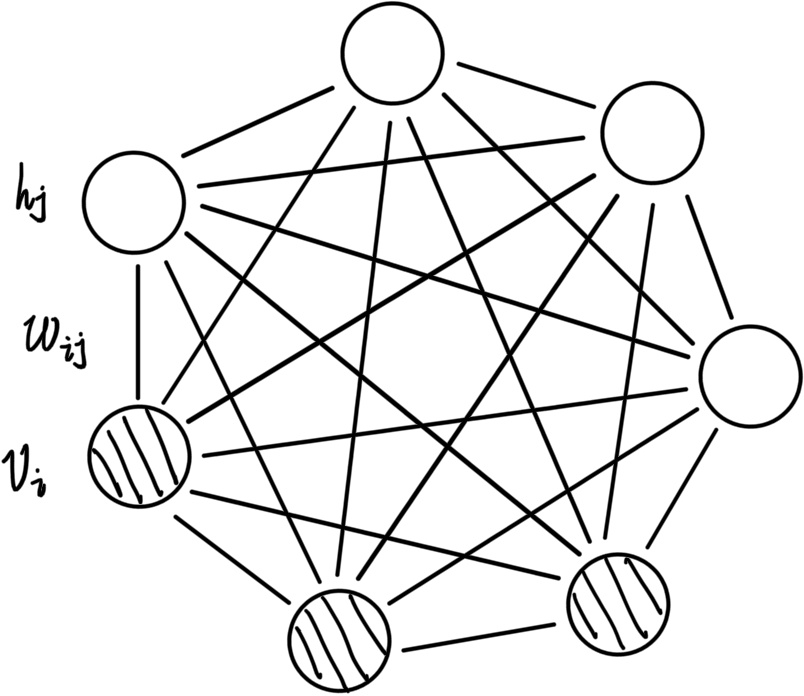
我们给其中的节点、连线做出一些定义：

1. 节点：观测节点 V = { 0 , 1 } D V = {\lbrace 0, 1 \rbrace}^D V={0,1}D，隐节点 H = { 0 , 1 } P H = {\lbrace 0, 1 \rbrace}^P H={0,1}P
2. 连线：观测节点之间$L=[L_{ij}{]}_{D\times D}$，隐节点之间$J=[J_{ij}{]}_{P\times P}$，观测节点与隐节点之间$W=[W_{ij}{]}_{D\times P}$
3. 参数： θ = { W , L , J } \theta = {\lbrace W, L, J \rbrace} θ={W,L,J}

则我们可以根据上面的定义，加上无向图能量方程的性质得到公式：
$$\{\begin{array}{l}P(V|H)=\frac{1}{z}exp-E(V,H)\\ E(V,H)=-(V^{T}WH+\underset{矩阵对称，参数除2}{\underbrace{\frac{1}{2}{V}^{T}LV+\frac{1}{2}{H}^{T}JH}})\end{array}$$

28.2 梯度推导

我们的目标函数就是$P(V)$，所以可以讲log-likelihood写作：$\frac{1}{N}{\sum }_{v\in V}\log P(v)$，并且$|V|=N$。所以我们可以将他的梯度写为$\frac{1}{N}{\sum }_{v\in V}{\nabla }_{\theta }\log P(v)$。其中${\nabla }_{\theta }\log P(v)$的推导在24-直面配分函数的RBM-Learning问题中已经推导过了，可以得到：
$${\nabla }_{\theta }\log P(v)=\sum _v\sum _{H}P(v,H)\cdot {\nabla }_{\theta }E(v,H)-\sum _{H}P(H|v)\cdot {\nabla }_{\theta }E(v,H)$$
我们对E(v, H)求其中一个参数的导的结果很容易求，所以可以将公式写作：
$$\begin{array}{rl}{\nabla }_w\log P(v)& =\sum _v\sum _{H}P(v,H)\cdot (-V{H}^T)-\sum _{H}P(H|v)\cdot (-V{H}^T)\\ & =\sum _{H}P(H|v)\cdot V{H}^T-\sum _v\sum _{H}P(v,H)\cdot V{H}^T\end{array}$$
将其带入原式可得：
$$\begin{array}{rl}{\nabla }_w\mathcal{L}& =\frac{1}{N}\sum _{v\in V}{\nabla }_{\theta }\log P(v)\\ & =\frac{1}{N}\sum _{v\in V}\sum _{H}P(H|v)\cdot V{H}^T-\underset{\frac{1}{N}\times N}{\underbrace{\frac{1}{N}\sum _{v\in V}}}\sum _v\sum _{H}P(v,H)\cdot V{H}^T\\ & =\frac{1}{N}\sum _{v\in V}\sum _{H}P(H|v)\cdot V{H}^T-\sum _v\sum _{H}P(v,H)\cdot V{H}^T\end{array}$$
我们用$P_{data}$表示$P_{data}(v,H)=P_{data}(v)\cdot P_{model}(H|v)$，$P_{model}$表示$P_{model}(v,H)$，则可以将公式再转化为：
$$\begin{array}{rl}{\nabla }_w\mathcal{L}& =E_{P_{data}}\left[V{H}^T\right]-E_{P_{model}}\left[V{H}^T\right]\end{array}$$

28.3 梯度上升

给三个参数分别写出他们的变化量（系数$\times$梯度）：
$$\{\begin{array}{l}\Delta W=\alpha (E_{P_{data}}\left[V{H}^T\right]-E_{P_{model}}\left[V{H}^T\right])\\ \Delta L=\alpha (E_{P_{data}}\left[V{V}^T\right]-E_{P_{model}}\left[V{V}^T\right])\\ \Delta J=\alpha (E_{P_{data}}\left[H{H}^T\right]-E_{P_{model}}\left[H{H}^T\right])\end{array}$$
这是用于表示在一次梯度上升中参数的改变量，由于$W,L,J$​是矩阵，将他们拆的更细可以写作：
$$\Delta w_{ij}=\alpha (\underset{\text{positive phase}}{\underbrace{E_{P_{data}}\left[v_i{h}_j\right]}}-\underset{\text{negative phase}}{\underbrace{E_{P_{model}}\left[v_i{h}_j\right]}})$$
但是这两项都很难求，因为要用到$P_{model}$，如果要得到$P_{model}$则要采用MCMC的方法，但对一个这样的图进行MCMC非常的消耗时间（不过这也给我们提供了一个解题思路）。

具体要用到MCMC的话，我们必须要有每一个维度的后验，所以我们根据复杂的推导（下面证明）可以得到每一个维度的后验——在固定其他维度求这一个维度的情况：
$$\{\begin{array}{l}P(v_i=1|H,V_{-i})=\sigma ({\sum }_{j=1}^P{w}_{ij}{h}_j+{\sum }_{k=1,-i}^D{L}_{ik}{v}_k)\\ P(h_j=1|V,H_{-j})=\sigma ({\sum }_{i=1}^P{w}_{ij}{v}_i+{\sum }_{m=1,-i}^D{J}_{jm}{h}_m)\end{array}$$
这个公式我们可以发现在RBM情况下也是符合RBM后验公式的。

---

接下来我们证明一下上面这个公式，下文验证$P(v_i|H,V_{-i})$的情况，$P(h_j|V,H_{-j})$​可以类比。首先对其进行变换：
P ( v i ∣ H , V − i ) = P ( H , V ) P ( H , V − i ) = 1 Z exp ⁡ { − E [ V , H ] } ∑ v i 1 Z exp ⁡ { − E [ V , H ] } = 1 Z exp ⁡ { V T W H + 1 2 V T L V + 1 2 H T J H } ∑ v i 1 Z exp ⁡ { V T W H + 1 2 V T L V + 1 2 H T J H } = 1 Z exp ⁡ { V T W H + 1 2 V T L V } ⋅ exp ⁡ { 1 2 H T J H } 1 Z exp ⁡ { 1 2 H T J H } ⋅ ∑ v i exp ⁡ { V T W H + 1 2 V T L V } = exp ⁡ { V T W H + 1 2 V T L V } ∑ v i exp ⁡ { V T W H + 1 2 V T L V } = exp ⁡ { V T W H + 1 2 V T L V } ∣ v i = 1 exp ⁡ { V T W H + 1 2 V T L V } ∣ v i = 0 + exp ⁡ { V T W H + 1 2 V T L V } ∣ v i = 1 \begin{align} P(v_i|H, V_{-i}) &= \frac{P(H, V)}{P(H, V_{-i})} \\ &= \frac{ \frac{1}{Z} \exp{\lbrace - E[V, H] \rbrace} }{ \sum_{v_i} \frac{1}{Z} \exp{\lbrace - E[V, H] \rbrace}} \\ &= \frac{ \frac{1}{Z} \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} + \frac{1}{2} {H^T J H} \rbrace} }{ \sum_{v_i} \frac{1}{Z} \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} + \frac{1}{2} {H^T J H} \rbrace}} \\ &= \frac{ \frac{1}{Z} \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace} \cdot \exp{\lbrace \frac{1}{2} {H^T J H} \rbrace} }{ \frac{1}{Z} \exp{\lbrace \frac{1}{2} {H^T J H} \rbrace} \cdot \sum_{v_i} \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace}} \\ &= \frac{ \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace} }{ \sum_{v_i} \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace}} \\ &= \frac{ \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace}|_{v_i = 1} }{ \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace}|_{v_i = 0} + \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace}|_{v_i = 1} } \\ \end{align} P(vi​∣H,V−i​)​=P(H,V−i​)P(H,V)​=∑vi​​Z1​exp{−E[V,H]}Z1​exp{−E[V,H]}​=∑vi​​Z1​exp{VTWH+21​VTLV+21​HTJH}Z1​exp{VTWH+21​VTLV+21​HTJH}​=Z1​exp{21​HTJH}⋅∑vi​​exp{VTWH+21​VTLV}Z1​exp{VTWH+21​VTLV}⋅exp{21​HTJH}​=∑vi​​exp{VTWH+21​VTLV}exp{VTWH+21​VTLV}​=exp{VTWH+21​VTLV}∣vi​=0​+exp{VTWH+21​VTLV}∣vi​=1​exp{VTWH+21​VTLV}∣vi​=1​​​​
若我们将相同的部份表示为${\Delta }_{v_i}$，则可以将公式写为：
$$\begin{array}{rl}P(v_i|H,V_{-i})& =\frac{{\Delta }_{v_i}{|}_{v_i=1}}{{\Delta }_{v_i}{|}_{v_i=0}+{\Delta }_{v_i}{|}_{v_i=1}}\end{array}$$
其中${\Delta }_{v_i}$可以做如下变换：
Δ v i = exp ⁡ { V T W H + 1 2 V T L V } = exp ⁡ { ∑ i ^ = 1 D ∑ j = 1 P v i ^ W i ^ j h j + 1 2 ∑ i ^ = 1 D ∑ k = 1 D v i ^ L i ^ k v k } \begin{align} \Delta_{v_i} &= \exp{\lbrace {V^T W H} + \frac{1}{2} {V^T L V} \rbrace} \\ &= \exp{\lbrace \sum_{{\hat i} = 1}^{D} \sum_{j = 1}^{P} {v_{\hat i} W_{{\hat i} j} h_j} + \frac{1}{2} \sum_{{\hat i} = 1}^{D} \sum_{k = 1}^{D} {v_{\hat i} L_{{\hat i} k} v_k} \rbrace} \end{align} Δvi​​​=exp{VTWH+21​VTLV}=exp{i^=1∑D​j=1∑P​vi^​Wi^j​hj​+21​i^=1∑D​k=1∑D​vi^​Li^k​vk​}​​
我们接下来将有$v_i$的项全部拆分出来：
Δ v i = exp ⁡ { ∑ i ^ = 1 , − i D ∑ j = 1 P v i ^ W i ^ j h j + ∑ j = 1 P v i W i j h j } ⋅ exp ⁡ { 1 2 ( ∑ i ^ = 1 , − i D ∑ k = 1 , − i D v i ^ W i ^ k h k + v i L i i v i ⏟ 0 + ∑ i ^ = 1 , − i D v i ^ W i ^ i v i ⏟ 相同 + ∑ k = 1 , − i D v i L i k v k ) } = exp ⁡ { ∑ i ^ = 1 , − i D ∑ j = 1 P v i ^ W i ^ j h j + ∑ j = 1 P v i W i j h j + 1 2 ∑ i ^ = 1 , − i D ∑ k = 1 , − i D v i ^ W i ^ k h k + ∑ k = 1 , − i D v i L i k v k } \begin{align} \Delta_{v_i} &= \exp{\lbrace \sum_{{\hat i} = 1, -i}^{D} \sum_{j = 1}^{P} {v_{\hat i} W_{{\hat i} j} h_j} + \sum_{j = 1}^{P} {v_i W_{i j} h_j} \rbrace} \\ & \cdot \exp{\lbrace \frac{1}{2} \left( \sum_{{\hat i} = 1, -i}^{D} \sum_{k = 1,-i}^{D} {v_{\hat i} W_{{\hat i} k} h_k} + \underbrace{v_i L_{ii} v_i}_{0} + \underbrace{\sum_{{\hat i} = 1, -i}^{D} {v_{\hat i} W_{{\hat i} i} v_i}}_{相同} + \sum_{k = 1, -i}^{D} {v_i L_{i k} v_k} \right) \rbrace} \\ &= \exp{\lbrace \sum_{{\hat i} = 1, -i}^{D} \sum_{j = 1}^{P} {v_{\hat i} W_{{\hat i} j} h_j} + \sum_{j = 1}^{P} {v_i W_{i j} h_j} + \frac{1}{2} \sum_{{\hat i} = 1, -i}^{D} \sum_{k = 1,-i}^{D} {v_{\hat i} W_{{\hat i} k} h_k} + \sum_{k = 1, -i}^{D} {v_i L_{i k} v_k} \rbrace} \end{align} Δvi​​​=exp{i^=1,−i∑D​j=1∑P​vi^​Wi^j​hj​+j=1∑P​vi​Wij​hj​}⋅exp{21​ ​i^=1,−i∑D​k=1,−i∑D​vi^​Wi^k​hk​+0 vi​Lii​vi​​​+相同 i^=1,−i∑D​vi^​Wi^i​vi​​​+k=1,−i∑D​vi​Lik​vk​ ​}=exp{i^=1,−i∑D​j=1∑P​vi^​Wi^j​hj​+j=1∑P​vi​Wij​hj​+21​i^=1,−i∑D​k=1,−i∑D​vi^​Wi^k​hk​+k=1,−i∑D​vi​Lik​vk​}​​
所以我们将$v_i=1$和$v_i=0$代入该公式即可得出结果。
Δ v i = 0 = exp ⁡ { ∑ i ^ = 1 , − i D ∑ j = 1 P v i ^ W i ^ j h j + 1 2 ∑ i ^ = 1 , − i D ∑ k = 1 , − i D v i ^ W i ^ k h k } = exp ⁡ { A + B } Δ v i = 1 = exp ⁡ { A + B + ∑ j = 1 P W i j h j + ∑ k = 1 , − i D L i k v k } \begin{align} \Delta_{v_i = 0} &= \exp{\lbrace \sum_{{\hat i} = 1, -i}^{D} \sum_{j = 1}^{P} {v_{\hat i} W_{{\hat i} j} h_j} + \frac{1}{2} \sum_{{\hat i} = 1, -i}^{D} \sum_{k = 1,-i}^{D} {v_{\hat i} W_{{\hat i} k} h_k} \rbrace} = \exp{\lbrace A + B \rbrace} \\ \Delta_{v_i = 1} &= \exp{\lbrace A + B + \sum_{j = 1}^{P} {W_{i j} h_j} + \sum_{k = 1, -i}^{D} {L_{i k} v_k} \rbrace} \end{align} Δvi​=0​Δvi​=1​​=exp{i^=1,−i∑D​j=1∑P​vi^​Wi^j​hj​+21​i^=1,−i∑D​k=1,−i∑D​vi^​Wi^k​hk​}=exp{A+B}=exp{A+B+j=1∑P​Wij​hj​+k=1,−i∑D​Lik​vk​}​​

P ( v i ∣ H , V − i ) = Δ v i ∣ v i = 1 Δ v i ∣ v i = 0 + Δ v i ∣ v i = 1 = exp ⁡ { A + B + ∑ j = 1 P W i j h j + ∑ k = 1 , − i D L i k v k } exp ⁡ { A + B } + exp ⁡ { A + B + ∑ j = 1 P W i j h j + ∑ k = 1 , − i D L i k v k } = exp ⁡ { ∑ j = 1 P W i j h j + ∑ k = 1 , − i D L i k v k } 1 + exp ⁡ { ∑ j = 1 P W i j h j + ∑ k = 1 , − i D L i k v k } = σ ( ∑ j = 1 P W i j h j + ∑ k = 1 , − i D L i k v k ) \begin{align} P(v_i|H, V_{-i}) &= \frac{ \Delta_{v_i}|_{v_i = 1} }{ \Delta_{v_i}|_{v_i = 0} + \Delta_{v_i}|_{v_i = 1} } \\ &= \frac{ \exp{\lbrace A + B + \sum_{j = 1}^{P} {W_{i j} h_j} + \sum_{k = 1, -i}^{D} {L_{i k} v_k} \rbrace} }{ \exp{\lbrace A + B \rbrace} + \exp{\lbrace A + B + \sum_{j = 1}^{P} {W_{i j} h_j} + \sum_{k = 1, -i}^{D} {L_{i k} v_k} \rbrace} } \\ &= \frac{ \exp{\lbrace \sum_{j = 1}^{P} {W_{i j} h_j} + \sum_{k = 1, -i}^{D} {L_{i k} v_k} \rbrace} }{ 1 + \exp{\lbrace \sum_{j = 1}^{P} {W_{i j} h_j} + \sum_{k = 1, -i}^{D} {L_{i k} v_k} \rbrace} } \\ &= \sigma(\sum_{j = 1}^{P} {W_{i j} h_j} + \sum_{k = 1, -i}^{D} {L_{i k} v_k}) \end{align} P(vi​∣H,V−i​)​=Δvi​​∣vi​=0​+Δvi​​∣vi​=1​Δvi​​∣vi​=1​​=exp{A+B}+exp{A+B+∑j=1P​Wij​hj​+∑k=1,−iD​Lik​vk​}exp{A+B+∑j=1P​Wij​hj​+∑k=1,−iD​Lik​vk​}​=1+exp{∑j=1P​Wij​hj​+∑k=1,−iD​Lik​vk​}exp{∑j=1P​Wij​hj​+∑k=1,−iD​Lik​vk​}​=σ(j=1∑P​Wij​hj​+k=1,−i∑D​Lik​vk​)​​

28.4 基于VI[平均场理论]求解后验概率

我们的参数，通过梯度求出的变化量可以表示为：
$$\{\begin{array}{l}\Delta W=\alpha (E_{P_{data}}\left[V{H}^T\right]-E_{P_{model}}\left[V{H}^T\right])\\ \Delta L=\alpha (E_{P_{data}}\left[V{V}^T\right]-E_{P_{model}}\left[V{V}^T\right])\\ \Delta J=\alpha (E_{P_{data}}\left[H{H}^T\right]-E_{P_{model}}\left[H{H}^T\right])\end{array}$$
但是如果要直接求出其后验概率，还应该从$\mathcal{L}=ELBO$开始分析，通过平均场理论（在VI中使用过）进行分解：
$$\begin{array}{rl}\mathcal{L}& =ELBO=\log P_{\theta }(V)-KL(q_{\varphi }\Vert p_{\theta })=\sum _h{q}_{\varphi }(H|V)\cdot \log P_{\theta }(V,H)+H[q]\end{array}$$
我们在这里做出一些假设（将$q(H|V)$拆分为P个维度之积）：
{ q ϕ ( H ∣ V ) = ∏ j = 1 P q ϕ ( H j ∣ V ) q ϕ ( H j = 1 ∣ V ) = ϕ j ϕ = { ϕ j } j = 1 P \begin{cases} q_\phi(H|V) = \prod_{j=1}^{P} q_\phi(H_j|V) \\ q_\phi(H_j = 1| V) = \phi_j \\ \phi = \{\phi_j\}_{j=1}^P \\ \end{cases} ⎩ ⎨ ⎧​qϕ​(H∣V)=∏j=1P​qϕ​(Hj​∣V)qϕ​(Hj​=1∣V)=ϕj​ϕ={ϕj​}j=1P​​
如果我们要求出后验概率就是学习参数$\theta$，在之类也等同于学习参数$\varphi$，于是我们可以对$arg{\max }_{{\varphi }_j}\mathcal{L}$​进行求解，我们将其进行化简：
$$\begin{array}{rl}\widehat{{\varphi }_j}& =arg\underset{{\varphi }_j}{\max }\mathcal{L}=arg\underset{{\varphi }_j}{\max }ELBO\\ & =arg\underset{{\varphi }_j}{\max }\sum _h{q}_{\varphi }(H|V)\cdot \log P_{\theta }(V,H)+H[q]\\ & =arg\underset{{\varphi }_j}{\max }\sum _h{q}_{\varphi }(H|V)\cdot \left[-\log Z+V^{T}WH+\frac{1}{2}{V}^{T}LV+\frac{1}{2}{H}^{T}JH\right]+H[q]\\ & =arg\underset{{\varphi }_j}{\max }\underset{=1}{\underbrace{\sum _h{q}_{\varphi }(H|V)}}\cdot \underset{\text{与h和ϕj都无关，为常数C}}{\underbrace{\left[-\log Z+\frac{1}{2}{V}^{T}LV\right]}}+\sum _h{q}_{\varphi }(H|V)\cdot \left[V^{T}WH+\frac{1}{2}{H}^{T}JH\right]+H[q]\\ & =arg\underset{{\varphi }_j}{\max }\sum _h{q}_{\varphi }(H|V)\cdot \left[V^{T}WH+\frac{1}{2}{H}^{T}JH\right]+H[q]\\ & =arg\underset{{\varphi }_j}{\max }\underset{(1)}{\underbrace{\sum _h{q}_{\varphi }(H|V)\cdot V^{T}WH}}+\underset{(2)}{\underbrace{\frac{1}{2}\sum _h{q}_{\varphi }(H|V)\cdot H^{T}JH}}+\underset{(3)}{\underbrace{H[q]}}\end{array}$$
得到如上公式后，我们只需对每个部份进行求导即可得到结果，过程中引入假设（拆分维度）即可更加优化公式，我们以$(1)$为例：
$$\begin{array}{rl}(1)& =\sum _h{q}_{\varphi }(H|V)\cdot V^{T}WH=\sum _h\prod _{\hat{j}=1}^P{q}_{\varphi }(H_{\hat{j}}|V)\cdot \sum _{i=1}^D\sum _{\hat{j}=1}^P{v}_i{w}_{i\hat{j}}{h}_{\hat{j}}\end{array}$$
我们取出其中的一项，如$i=1,\hat{j}=2$，可以得到：
$$\begin{array}{rl}\sum _h\prod _{\hat{j}=1}^P{q}_{\varphi }(H_{\hat{j}}|V)\cdot v_1{w}_{12}{h}_2& =\underset{\text{提出h2相关项}}{\underbrace{\sum _{h_2}{q}_{\varphi }(H_2|V)\cdot v_1{w}_{12}{h}_2}}\cdot \underset{=1}{\underbrace{\sum _{h,-h_2}\prod _{\hat{j}=1,-2}^P{q}_{\varphi }(H_{\hat{j}}|V)}}\\ & =\sum _{h_2}{q}_{\varphi }(H_2|V)\cdot v_1{w}_{12}{h}_2\\ & =q_{\varphi }(H_2=1|V)\cdot v_1{w}_{12}\cdot 1+q_{\varphi }(H_2=0|V)\cdot v_1{w}_{12}\cdot 0\\ & ={\varphi }_2{v}_1{w}_{12}\end{array}$$
所以$(1)$的求和结果就应该是${\sum }_{i=1}^D{\sum }_{\hat{j}=1}^P{\varphi }_{\hat{j}}{v}_i{w}_{i\hat{j}}$，同理可得$(2),(3)$结果为：
$$\{\begin{array}{l}(1)={\sum }_{i=1}^D{\sum }_{\hat{j}=1}^P{\varphi }_{\hat{j}}{v}_i{w}_{i\hat{j}}\\ (2)={\sum }_{\hat{j}=1}^P{\sum }_{m=1,-j}^P{\varphi }_{\hat{j}}{\varphi }_m{J}_{\hat{j}m}+C\\ (3)=-{\sum }_{j=1}^P\left[{\varphi }_j\log {\varphi }_j+(1-{\varphi }_j)\log (1-{\varphi }_j)\right]\end{array}$$
通过求导又可得：
$$\{\begin{array}{l}{\nabla }_{{\varphi }_j}(1)={\sum }_{i=1}^D{v}_i{w}_{ij}\\ {\nabla }_{{\varphi }_j}(2)={\sum }_{m=1,-j}^P{\varphi }_m{J}_{jm}\\ {\nabla }_{{\varphi }_j}(3)=-\log \frac{{\varphi }_j}{1-{\varphi }_j}\end{array}$$
根据${\nabla }_{{\varphi }_j}(1)+{\nabla }_{{\varphi }_j}(2)+{\nabla }_{{\varphi }_j}(3)=0$可得：
$${\varphi }_j=\sigma (\sum _{i=1}^D{v}_i{w}_{ij}+\sum _{m=1,-j}^P{\varphi }_m{J}_{jm})$$
由于${\varphi }_j$用于表示每一个维度的数据，所以我们可以使用 ϕ = { ϕ j } j = 1 P \phi = \{\phi_j\}_{j=1}^{P} ϕ={ϕj​}j=1P​通过坐标上升的方法进行求解。