进程的退出分为正常退出和异常退出:
正常退出
- Main函数调用return
- 进程调用exit(),标准c库
- 进程调用_exit()或_Exit(),属于系统调用
- 进程最后一个线程返回(之后学到)
- 最后一个线程调用pthread_exit(之后学到)
异常退出
- 调用abort
- 当进程收到某些信号时,比如strl+C
- 最后一个线程对取消(cancellation)请求做出响应(之后学到)

exit()
需要包含的头文件:
#include <stdlib.h>函数原型:
void exit(int status);_exit()
需要包含的头文件:
#include <unistd.h>函数原型:
void _exit(int status);_Exit()
需要包含的头文件:
#include <stdlib.h>函数原型:
void _Exit(int status);可见,三种exit虽然名字不同,所需的头文件也不尽相同,但是参数都是完全相同的,这个int型的status就是状态码


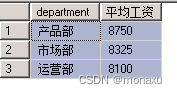
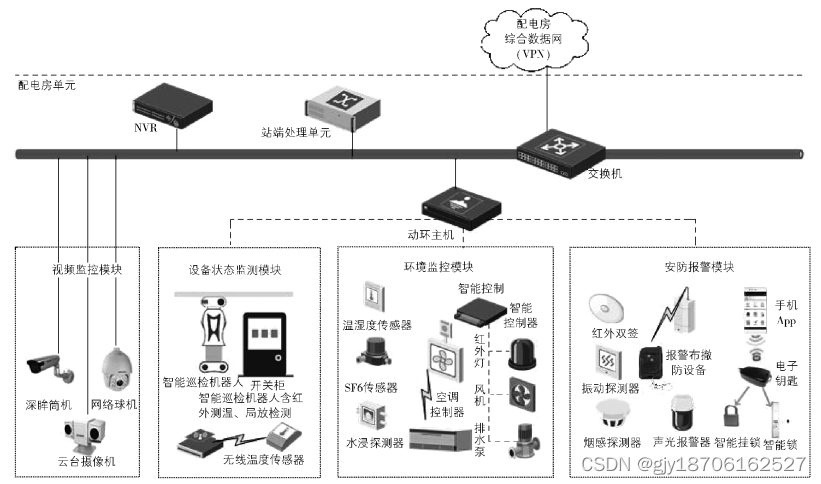
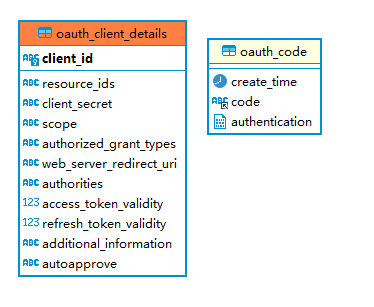




![[Leetcode] [Tutorial] 回溯](https://img-blog.csdnimg.cn/b704acb8f66d45eb9fb9c4bf7e2682e9.png#pic_center)