0 提纲

4.1 logistic回归
4.2 支持向量机(SVM)
4.3 PCA

1 logistic回归

用超平面分割正负样本, 考虑所有样本导致的损失.

1.1 线性分类器

logistic 回归是使用超平面将空间分开, 一边是正样本, 另一边是负样本. 因此, 它是一个线性分类器.
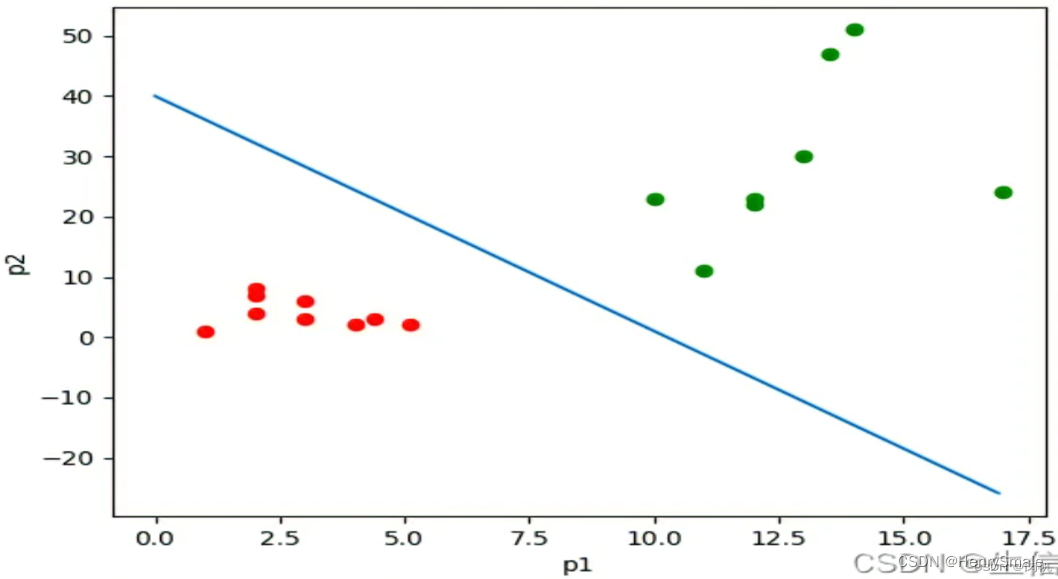
如图所示, 若干样本由两个特征描述, 对应于二维平面上的点.

• 它们为正样本或负样本, 由不同颜色表示.
• 现在需要使用一条直线将正、负样本分开. 这样, 对于新的样本, 就看它落在直线的哪一边, 由此判断正负.
• 这条直线就是线性分类器. 显然, 对于更高维的数据, 其线性分类器就是一个超平面.

• 输入：数据矩阵$\mathbf{X}=(x_{ij}{)}_{n\times m}\in {\mathbb{R}}^{n\times m}$, 二分类标签向量 Y = ( y i ) n × 1 ∈ { 0 , 1 } n \mathbf{Y} = (y_i)_{n \times 1} \in \{0, 1\}^n Y=(yi​)n×1​∈{0,1}n.
• 输出：$m$维空间上的一个超平面$\mathbf{wx}=0$, 其中$\mathbf{w},\mathbf{x}\in {\mathbb{R}}^{m+1}$
• 优化目标：
  $$\max \prod ^{n}h({\mathbf{x}}_i{)}^{y_i}(1-h({\mathbf{x}}_i){)}^{1-y_i}$$
  其中， x i = { x i 1 , x i 2 , … , x i m } \mathbf{x}_i = \{x_{i1}, x_{i2}, \dots, x_{im}\} xi​={xi1​,xi2​,…,xim​}, ${\mathbb{R}}^{m+1}$增加的一维用于处理常数偏移量，这与线性回归的方式相同；$h({\mathbf{x}}_i)=\frac{1}{1+e^{-{\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_i}}$为sigmoid函数，它将取值范围为$(-\infty ,\infty )$的${\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_i$压缩到取值范围为$(0,1)$的$h({\mathbf{x}}_i)$, 可以解释为正例的概率.

指数有巧妙的设置, 把两种情况统一起来了

• 当$y_i=0$ (为负例) 时, 优化目标中的 $(1-h(x_i))$ 起作用, 即预测值越小, 相应项越大;
• 当$y_i=1$ (为正例) 时, 优化目标中的 $h(x_i)$ 起作用, 即预测值越大, 相应项越大.
• 连乘是通过极大似然估计推导出来的, 概率的乘积还是概率;
• $\max$ 表示的是 极大似然估计.

1.2 方案说明

方案和问题定义相同. 这是因为问题定义成这样, 方案也就固定了.
使用 sigmoid 函数的原因, 以及极大似然估计的推导：https://blog.csdn.net/weixin_60737527/article/details/124141293
每个点对优化目标都有贡献 (后面讲到 SVM 会回顾这里).

• 如果远离分割面而且分类正确, 则相应项接近 1;
• 如果远离分割面而且分类错误, 则相应项接近 0.

极大似然估计, 在机器学习中频繁被用到. 其思想就是一个事件发生了，那么发生这个事件的概率就是最大的.

1.3 方案求解

连乘用 log 变成连加, log 是一个单调函数, 不影响最大化目标. 这也是常用招数.
对式子取对数。原公式求最大值，可以取对数后乘以负1,之后求最小值。
$$L(\mathbf{w})=\frac{1}{n}\sum _{i=1}^n-y_i\ln (h({\mathbf{x}}_i))-(1-y_i)\ln ((1-h({\mathbf{x}}_i)))$$
求最小值方法很多，机器学习中常用梯度下降系列方法。也可以采用牛顿法，或是求导数为零时$\mathbf{w}$的数值等。

1.4 与线性回归的联系与区别

联系: 都是线性模型, logistic 回归还被称为广义线性模型.
区别: logistic 回归是分类, 要把两个类别的点尽可能分开. 直观上来看, logistic 回归比线性回归靠谱. 不过二分类任务的输出只有两个值, 而线性回归的输出是一个实数值, 后者更难把握.

2 支持向量机(SVM)

用 (核函数升维后的) 超平面分割正负样本, 仅考虑所有边界样本 (支持向量) 导致的距离.

2.1 线性分类器

支持向量机 (support vector machine, SVM) 有很多闪光点, 理论方面有 VC 维的支撑, 技术上有核函数将线性不可分变成线性可分, 实践上是小样本学习效果最好的算法.
如图所示, 基础的 SVM 仍然是一个线性二分类器, 这一点与 logistic 回归一致.

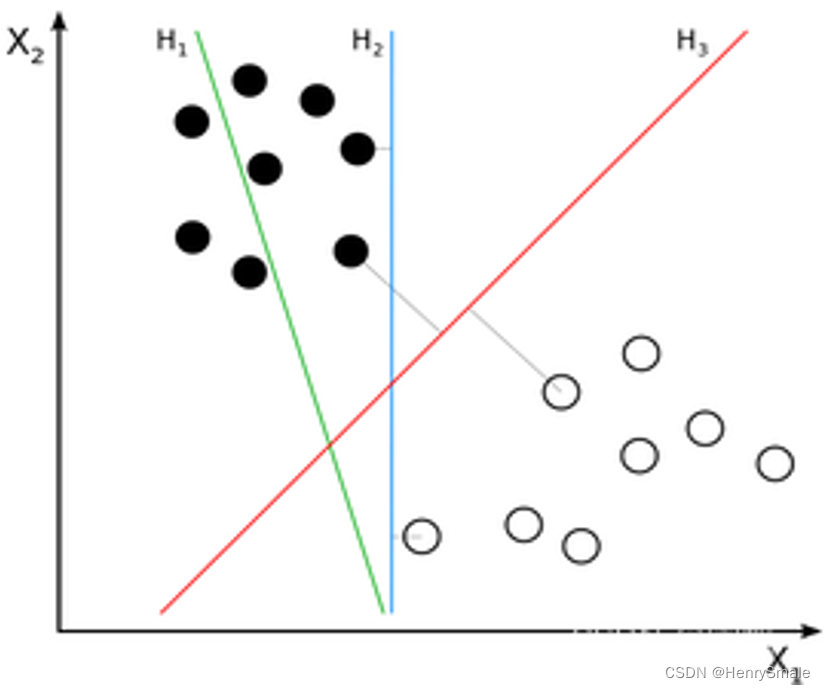
图 1 有 3 个分割线, 分别对应于一个分类器.

• H1不能把正负样本分开, 拟合能力弱;
• H2可以把正负样本分开 (拟合能力强), 但它与最近的正负样本距离小;
• H3可以把正负样本分开, 而且与最近的正负样本距离达到了最大, 因此它有良好的泛化能力, 即对于新样本的预测能力.

使用下图来说明.

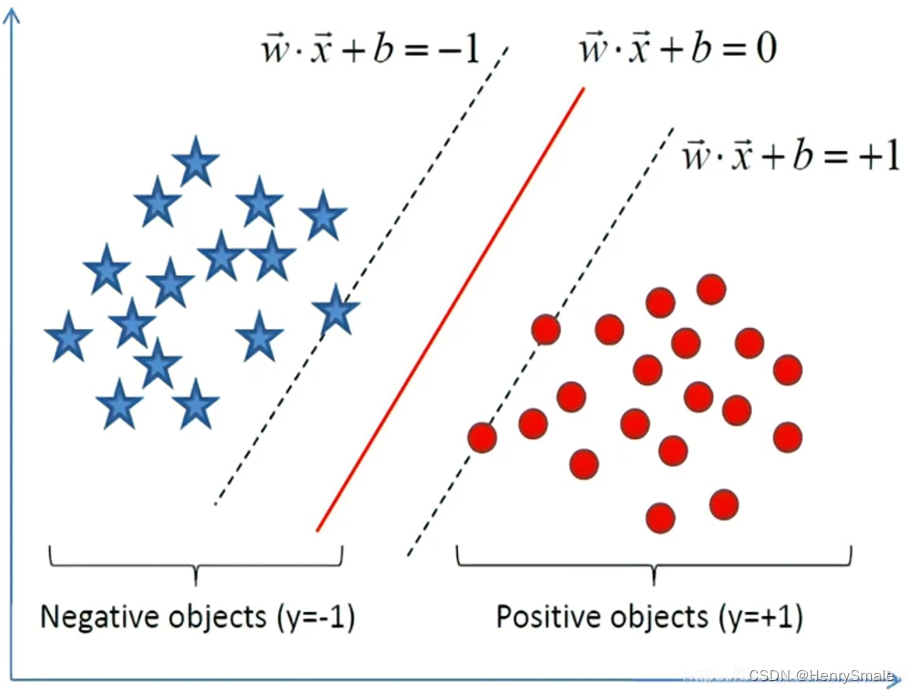
• 输入：数据矩阵$\mathbf{X}=(x_{ij}{)}_{n\times m}\in {\mathbb{R}}^{n\times m}$, 二分类标签向量 Y = ( y i ) n × 1 ∈ { − 1 , 1 } n \mathbf{Y} = (y_i)_{n \times 1} \in \{-1, 1\}^n Y=(yi​)n×1​∈{−1,1}n.
• 输出：$m$维空间上的一个超平面$\mathbf{wx}+b=0$, 其中$\mathbf{w},\mathbf{x}\in {\mathbb{R}}^m$
• 优化目标：
  $$\arg \underset{\mathbf{w},b}{\max }\frac{1}{||\mathbf{w}||}.(最大化实线到虚线的间隔)$$
• 约束条件：$y_i({\mathbf{w}}^{\mathbf{T}}\varphi ({\mathbf{x}}_i)+b)\ge 1$.

其中：

• 标签的取值范围为 { − 1 , + 1 } \{-1, +1\} {−1,+1}, 和 logistic 回归的 { 0 , 1 } \{0, 1\} {0,1}不同. 这是为了表达相应的式子方便;
• 优化目标是最大化实线到虚线的间隔;
• 约束条件是每个样本点被正确分类 (为正数), 且到实线的加权距离不小于 1.

2.2 基本方案

实线对应的是线性分类器, 即分割超平面;
虚线上的点被称为支持向量 (support vector), 也就是关键样本的意思, 因为样本在空间用向量表示;
支持向量之外的样本, 最终没有为分类器作出贡献. 这是与 logistic 回归一个本质的区别.

2.3 核函数

用核函数将低维空间的数据映射到高维空间, 这样, 以前线性不可分的数据就变得线性可分.
这是一个神奇的想法, 因为机器学习很多时候致力于将高维数据降为低维 (如 PCA, 这个我们后面说), 而 SVM 反其道而行的.

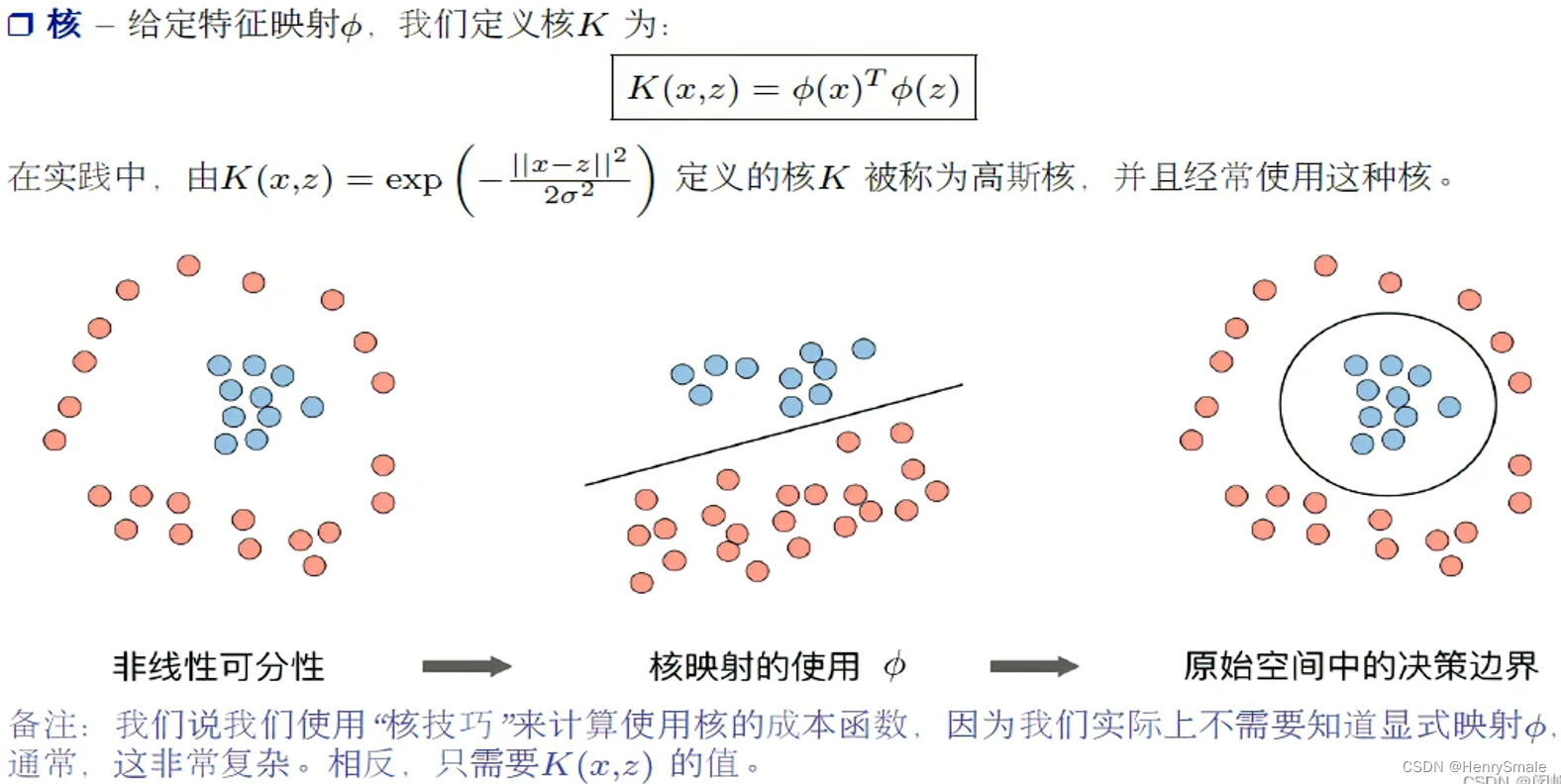
• 原始数据点是线性不可分的 (即二维平面上的任意直线都不可能把两种类别的数据点分开). 但使用高斯核将数据映射到三维就可以做到用二维平面分割.
• 想像下某人脸上有痘痘, 如果脸部看作一个平面, 则去掉痘痘不可避免需要画一个圈, 它不是线性的. 现在逮住痘痘的中间往外面拉, 将脸部拉成一个曲面, 这时候, 用一把手术刀进行切割 (对应于一个平面), 就可以把痘痘切下来啦. 这真是一个不忍直视的画面 😦.

下图给出了更直观的画面.

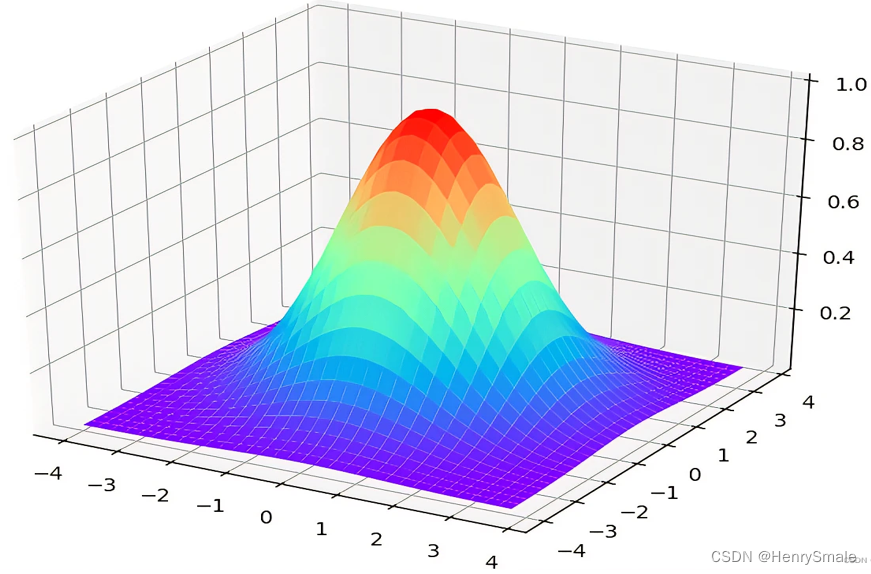
常用的核函数有：线性核，多项式核，高斯核，Sigmoid核和复合核，傅立叶级数核，B样条核和张量积核等。还有很多核函数. 甚至有人将核技巧弄出来之后, 脱离了 SVM 进行使用. 这是 2000 年前后的研究热点.

2.4 软间隔

有时候某些正负样本实在无法从对方阵营里面分出来, 即 (2) 式所表达的约束条件无法得到满足, 就可以使用软间隔.
引入松弛变量${\xi }_i\ge 0$，允许SVM在一些样本上出错，约束条件改为：
$$y_i({\mathbf{w}}^{\mathbf{T}}\varphi ({\mathbf{x}}_i)+b)\ge 1-{\xi }_i$$

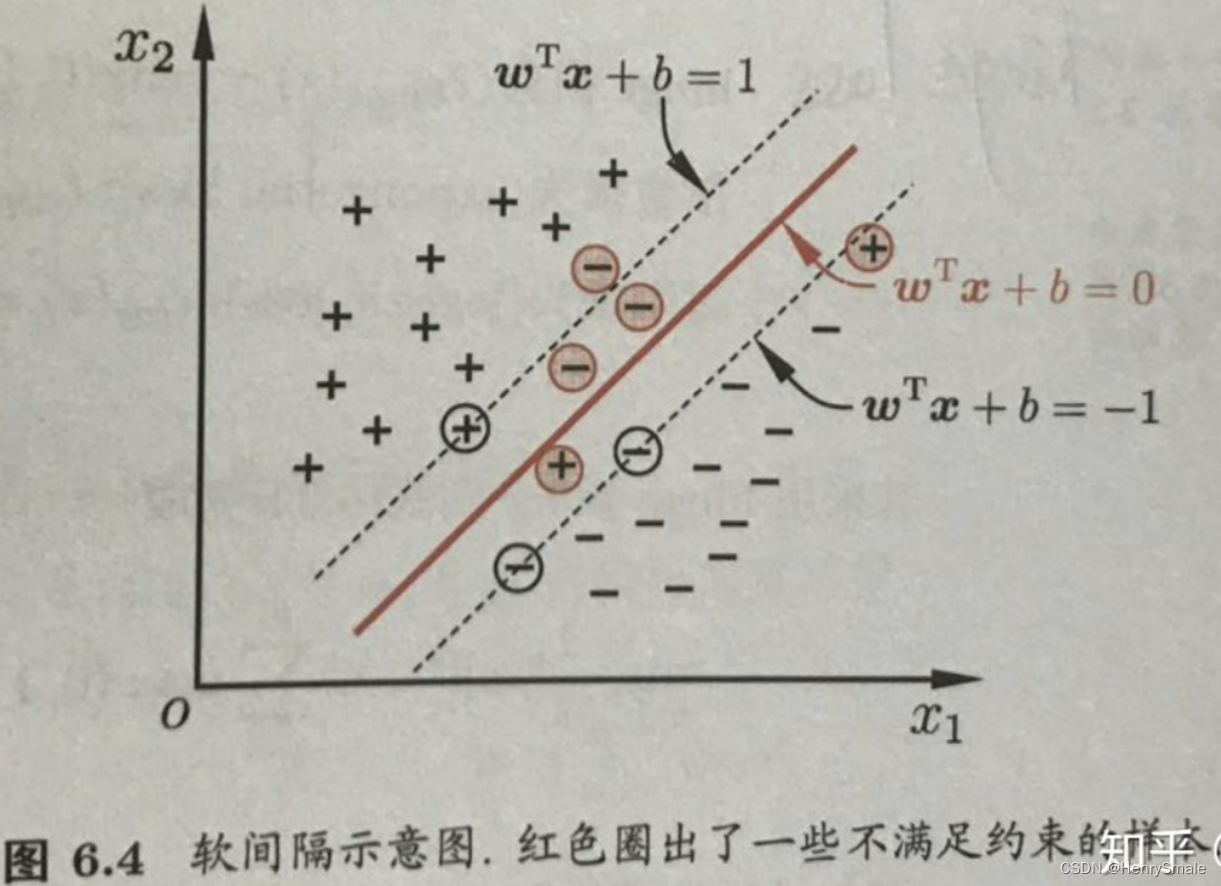
2.5 讨论

一个数据集应该使用什么核函数, 经常是试出来的. 这个和神经网络调参类似, 不是那么讲道理.
对于高维数据, 几十个支持向量很正常. 无论如何, 支持向量 (样本) 都只占训练集的一小部分.
支持向量机能很好地防止过拟合, 因为只要支持向量不改变, 其它样本的改变都不影响分类器. 当然, 这使得支持向量的选取 (与核函数的选取有关) 至关重要.

3 PCA

求特征值与特征向量, 以及相应的基向量, 进行空间的映射.

3.1 特征选择与特征提取

主成分分析 (principal component analysis, PCA) 是一种有理论依据的无监督特征提取的线性方法.
特征选择是指从已有的特征里面选择出一个子集. 例如: 身高、体重、性别、年龄、体温、血相等等, 如果要一个人是否患流感，身高、体重等不但没有作用, 反而还会让分类器效果变差. 回头想想 $k$NN, 在计算距离时考虑一些不相关的特征, 会使得相似的样本变得不相似.

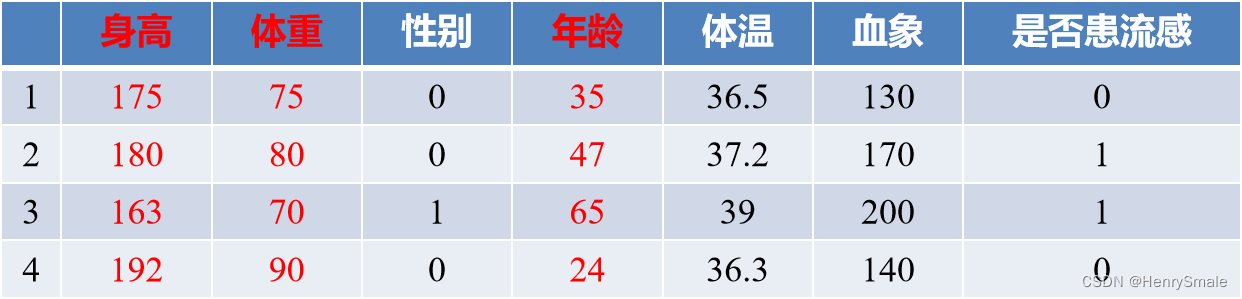
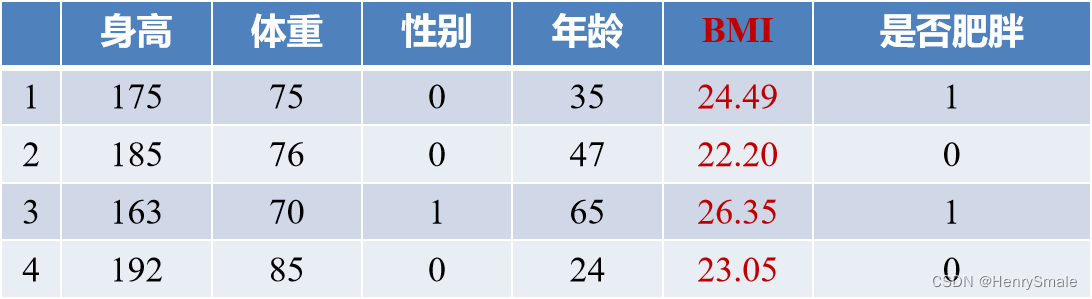
特征提取则是指从已有特征中生成新的特征. 例如: 人们常说自己有多重, 然后表达想减肥的意愿. 但这种想法是错误的, 应该计算 BMI(体重÷身高²), 以此确定自己是否偏胖. 这里 “计算 BMI”, 就是一个特征提取的过程.
总的来说, 特征选择相对简单, 而特征提取有很大的想像空间. 后面将会介绍的神经网络, 其最本质的任务就是特征提取.

3.2 PCA 的基本思想

PCA 有两个特点:

• 进行无监督的特征提取, 即它不考虑标签;
• 是一个线性模型, 即新特征均为原始特征的线性组合.

如图 1 所示, 二维平面上有一系列数据点.
从它们的角度来看, $x$轴和 $y$轴两个特征的区分能力都差不多, 特征的取值范围都是[−4,+4].

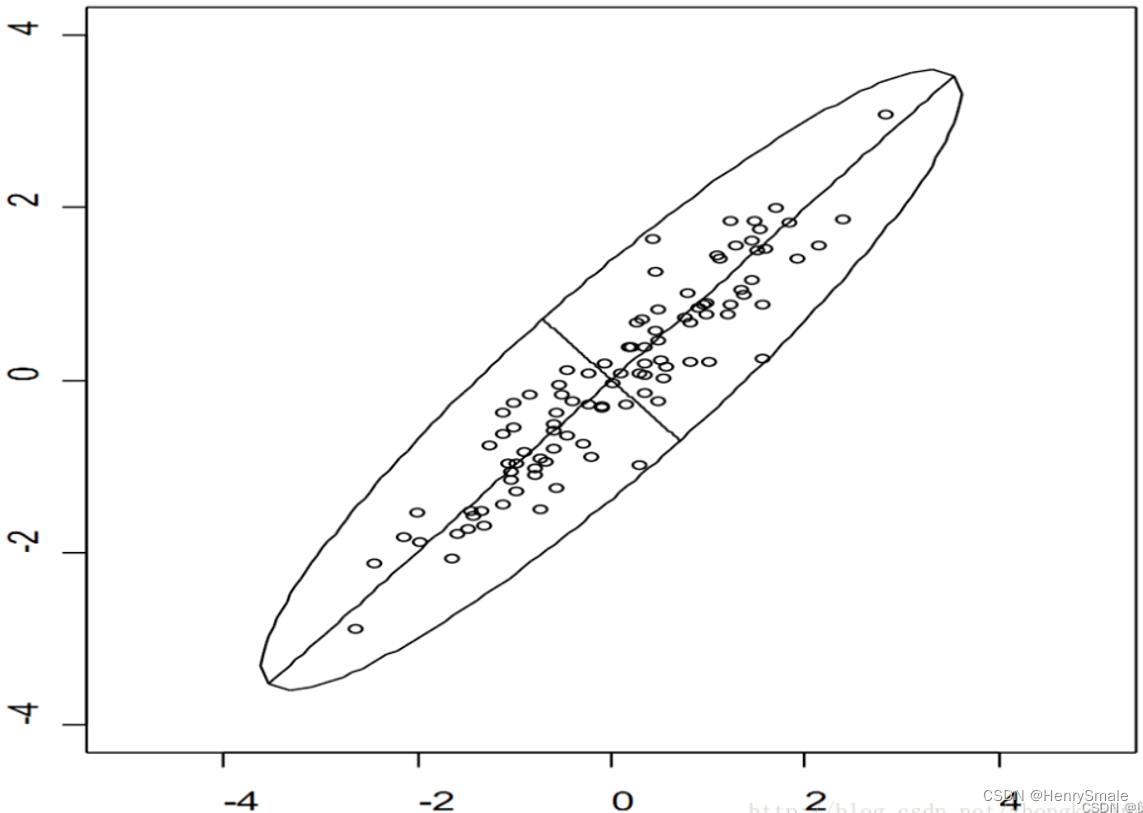
如果我们将这些点围绕原点顺时针旋转 45 度, 就会发现新的 $x$ 轴把样本分得比较开, 而新的 $y$ 轴区分能力比较弱.
再想像一个极端的情况: 这些点全部在一条直线上, 经过旋转后 $x$ 轴起到作用, 而$y$ 轴完全没有区分能力.

从高等数学的角度, 就是需要求一组正交基, 且排名靠前的基向量 (被称为 主成分) 区分能力更强. 这组正交基的个数有可能少于原始空间的维度, 这时就达到 特征提取 + 降维 的作用.

为了进一步地降维, 设置一个阈值, 将基向量的区分度低于该域值时, 就可以把它抛弃.

3.3 PCA计算过程

参考：https://www.cnblogs.com/hadoop2015/p/7419087.html
问题: 真实的训练数据总是存在各种各样的问题, 比如拿到一个汽车的样本，里面既有以“千米/每小时”度量的最大速度特征，也有“英里/小时”的最大速度特征，显然这两个特征有一个多余。.
PCA的思想是将$n$维特征映射到$k$维上($k<n$)，这$k$维是全新的正交特征。这k维特征称为主元，是重新构造出来的$k$维特征，而不是简单地从$n$维特征中去除其余$n-k$维特征。
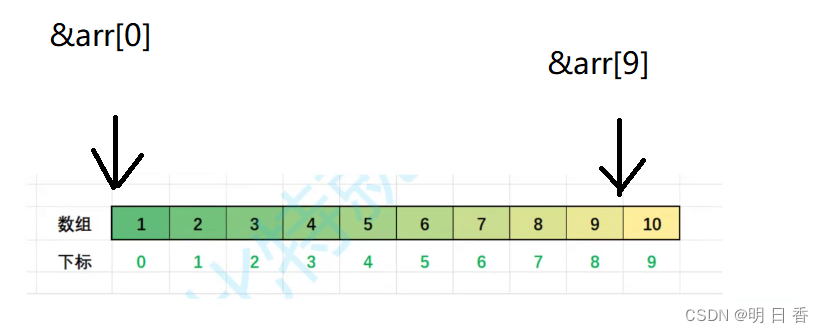
假设我们得到的2维数据。
有10个样例，每个样例两个特征。可以这样认为，有10篇文档，$x$是10篇文档中“learn”出现的TF-IDF，$y$是10篇文档中“study”出现的TF-IDF。也可以认为有10辆汽车，$x$是千米/小时的速度，$y$是英里/小时的速度

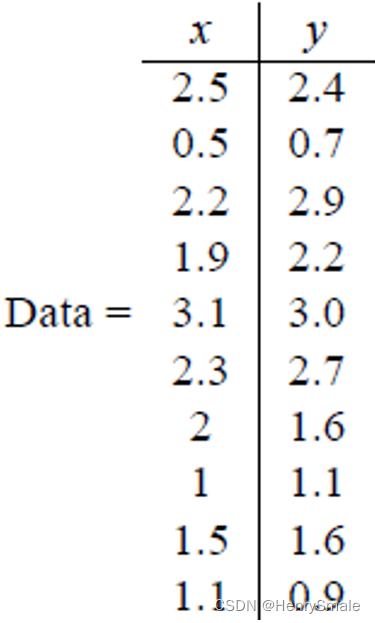
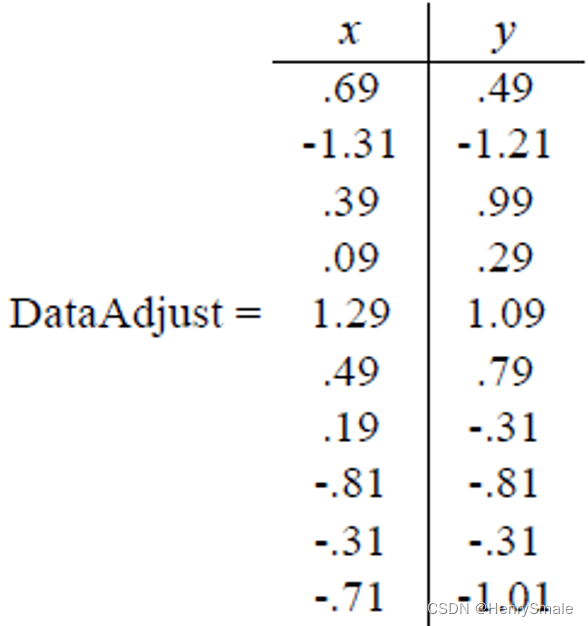
• 第一步分别求x和y的平均值，然后对于所有的样例，都减去对应的均值。这里x的均值是1.81，y的均值是1.91，那么一个样例减去均值后即为（0.69,0.49），得到：
  
• 第二步，求特征协方差矩阵，如果数据是3维，那么协方差矩阵是：
  

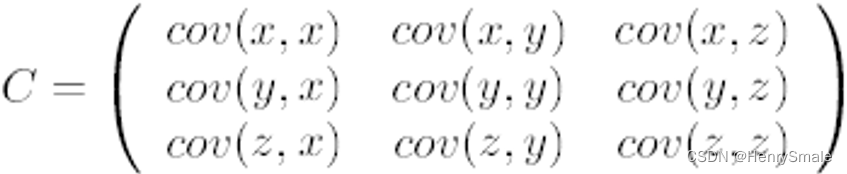
这里只有$x$和$y$，求解得：

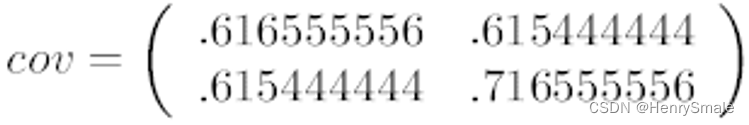
对角线上分别是$x$和$y$的方差，非对角线上是协方差。

• 协方差大于0表示$x$和$y$若有一个增，另一个也增；小于0表示一个增，一个减；协方差为0时，两者独立。

• 协方差绝对值越大，两者对彼此的影响越大，反之越小。

• 第三步，利用矩阵的知识，求协方差矩阵 $\mathbf{C}$的特征值 $\lambda$ 和相对应的特征向量 $\mathbf{u} $每一个特征值对应一个特征向量）
  $$\mathbf{Cu}=\lambda \mathbf{u}$$
  
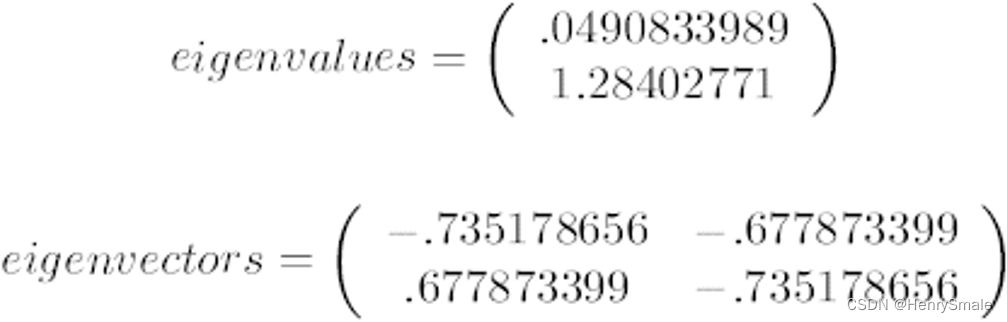
  上面是两个特征值，下面是对应的特征向量，特征值0.0490833989对应特征向量为 $(-0.735148656,0.677873399)$，这里的特征向量都归一化为单位向量。

• 第四步，将特征值按照从大到小的顺序排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
  这里特征值只有两个，我们选择其中最大的那个，这里是1.28402771，对应的特征向量是(-0.677873399, -0.735148656).
  -第五步，将样本点投影到选取的特征向量上。假设样例数为m，特征数为n，减去均值后的样本矩阵为DataAdjust(mn)，协方差矩阵是nn，选取的k个特征向量组成的矩阵为EigenVectors(nk)。那么投影后的数据FinalData为:
  $$FinalData(m\ast k)=DataAdjust(m\ast n)\times EigenVectors(n\ast k)$$
  FinalData(101) = DataAdjust(10*2矩阵)×特征向量(-0.677873399, -0.735148656), 得到结果是:
  
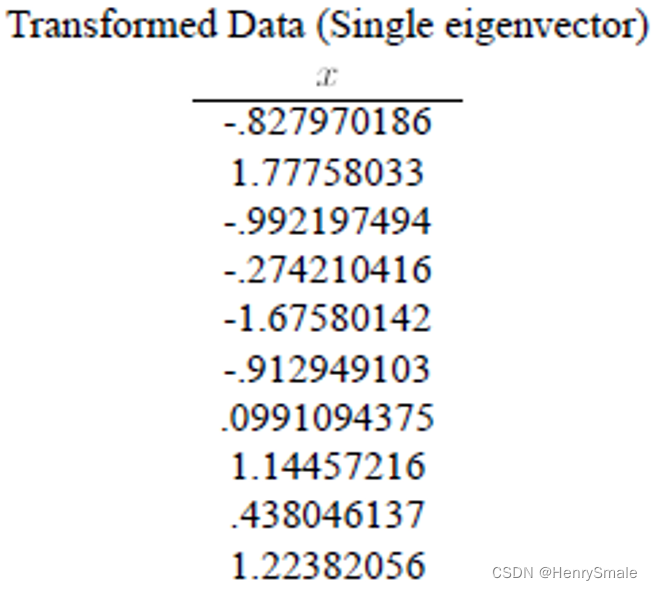
  这样，就将原始样例的n维特征变成了k维，这k维就是原始特征在k维上的投影。
  上面的数据可以认为是learn和study特征融合为一个新的特征叫做LS特征，该特征基本上代表了这两个特征。
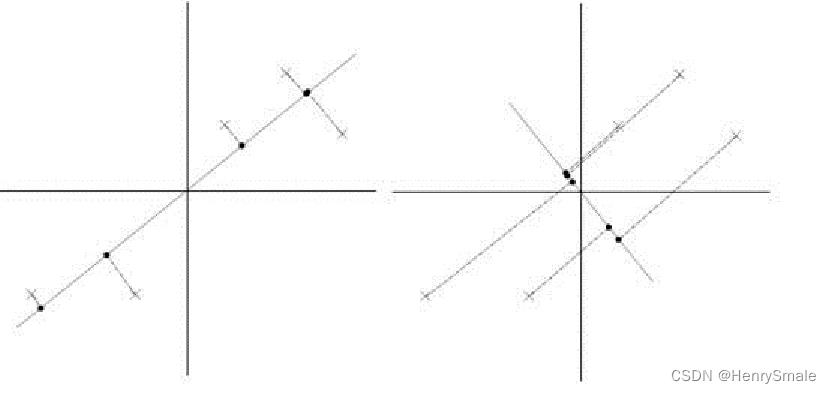
  上述过程有个图描述：
  
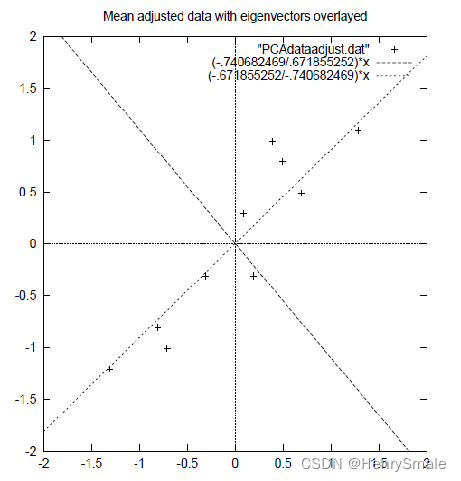
  正号表示预处理后的样本点，斜着的两条线就分别是正交的特征向量（由于协方差矩阵是对称的，因此其特征向量正交），最后一步的矩阵乘法就是将原始样本点分别往特征向量对应的轴上做投影。

3.4 最大方差理论

要解释为什么协方差矩阵的特征向量就是k维理想特征，需要了解最大方差理论。
在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。
如前面的图，样本在横轴上的投影方差较大，在纵轴上的投影方差较小，那么认为纵轴上的投影是由噪声引起的。
因此我们认为，最好的k维特征是将n维样本点转换为k维后，每一维上的样本方差都很大。
比如下图有5个样本点：（已经做过预处理，均值为0，特征方差归一化）,下面将样本投影到某一维上，这里用一条过原点的直线表示。

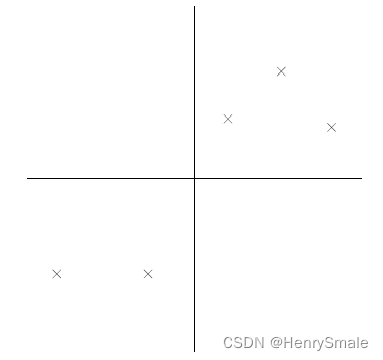
假设我们选择两条不同的直线做投影，那么左右两条中哪个好呢？根据我们之前的方差最大化理论，左边的好，因为投影后的样本点之间方差最大。

3.5 PCA优缺点

优点

• 有良好的数学基础;
• 有良好的应用.
  缺点：
• 只是一个线性模型;
• 只能做简单的数据预处理;
• 无监督模型, 不一定适用于有监督数据.