一.举例通俗解释ResNet思想
假设你正在学习如何骑自行车,并且想要骑到一个遥远的目的地。你可以选择直接骑到目的地,也可以选择在途中设置几个“中转站”,每个中转站都会告诉你如何朝着目的地前进。
在传统的神经网络中,就好比只能选择直接骑到目的地。当你的目的地很远时,可能会出现骑不到目的地的情况,因为网络在训练过程中无法有效地传递信息,导致梯度消失或梯度爆炸。
而ResNet则是在途中设置多个**“残差块”作为中转站**。每个残差块相当于一个中转站。
二.ResNet网络结构

假设f(x)是最终求得的函数。ResNet把函数拆成了f(x) = x + g(x).

传统网络相当于直接达到目的地,就是直接求f(x)。
ResNet是先到达一个中转站,即先求得g(x),再求g(x) + x 得到f(x)。同时可以推出g(x) = f(x) - x。
三.用实际的数举例子:
假设要求的f(x) = 5x^2 + 3x +2
ResNet先求得 g(x) = f(x) - x = 5x^2 + 2x +2 ,然后将g(x) 与x相加,最终得到f(x)=g(x) + x = 5x^2 + 3x +2
四.为什么ResNet非要设计成先求一个中转的函数g(x),然后再加上x呢?
4.1 解决网络加深,效果变差的问题

假如输入的x已经是最好的结果,如果加深网络效果会变差,即把最好的结果x输入到新一层的网络g(x)中,效果会变差。
那么我们直接令g(x)=0,相当于舍弃掉影响最优结果的网络块。最终得到的f(x) = 0 +x,保留了最优结果x。
从反向传播的角度来说,解决梯度消失和梯度爆炸的问题

对y=F(x)+x求偏导发现会出现画圈的地方,梯度消失是累积的乘积中出现接近0的数,影响梯度的结果,梯度爆炸是累积乘积,结果出现指数级增长。多了画圈地方的+操作,就打破了累乘,结果不容易出现梯度消失与爆炸。
五.代码实现
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
import time
class Residual(nn.Module):
def __init__(self,input_channels,num_channels,use_1x1conv=False,strides=1):
super().__init__()
self.conv1 = nn.Conv2d(input_channels,num_channels,kernel_size=3,padding=1,stride=strides)
self.conv2 = nn.Conv2d(num_channels,num_channels,kernel_size=3,padding=1)
if use_1x1conv: # 使用1x1卷积核控制输出通道数
self.conv3 = nn.Conv2d(input_channels,num_channels,kernel_size=1,stride=strides)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(num_channels)
self.bn2 = nn.BatchNorm2d(num_channels)
def forward(self,X):
Y = F.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3: # 用1x1卷积将x通道与形状 调整的与 f(x)-x一致
X = self.conv3(X)
# 不用1x1调整通道时直接 y+X = = f(x)-X + X
Y += X
return F.relu(Y)
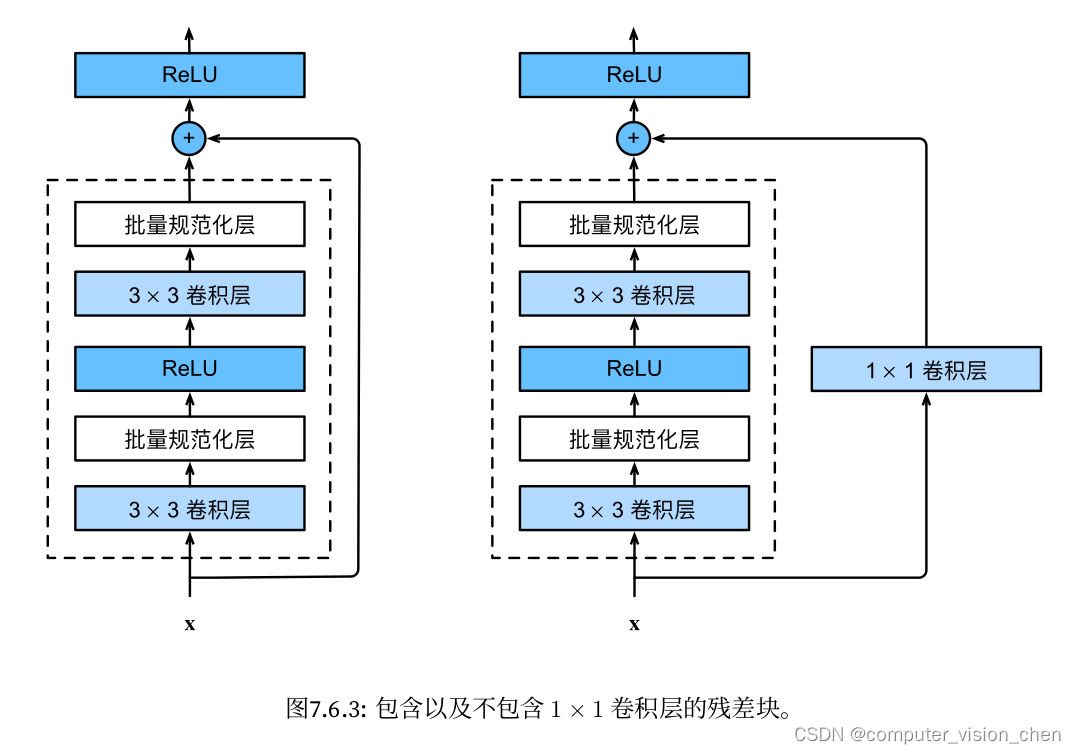
包含以及不包含 1 × 1 卷积层的残差块
此代码生成两种类型的网络:一种是当use_1x1conv=False时,应用ReLU非线性函数之前,
将输入添加到输出。另一种是当use_1x1conv=True时,添加通过1 × 1卷积调整通道和分辨率。
blk = Residual(input_channels=3,num_channels=3)
X = torch.rand(4, 3, 6, 6)
Y = blk(X)
Y.shape
torch.Size([4, 3, 6, 6])
# 使用1x1卷积控制通道数,使用strides=2减半输出的高和宽,num_channels是输出的通道数
blk = Residual(input_channels=3,num_channels=6, use_1x1conv=True, strides=2)
blk(X).shape
torch.Size([4, 6, 3, 3])
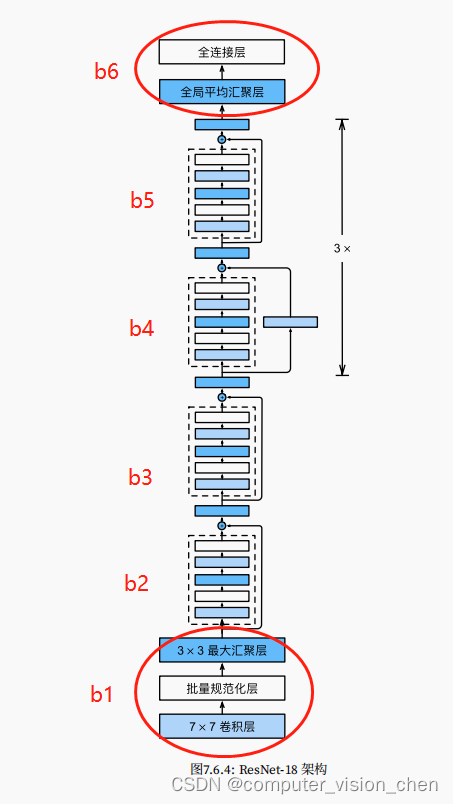
ResNet模型架构
#ResNet模型
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
# 残差块
def resnet_block(input_channels, num_channels, num_residuals,first_block=False):
blk = []
for i in range(num_residuals):
if i == 0 and not first_block:
blk.append(Residual(input_channels, num_channels,
use_1x1conv=True, strides=2))
else:
blk.append(Residual(num_channels, num_channels))
return blk
# 接着在ResNet加入所有残差块,这里每个模块使用2个残差块。
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))
# 最后,与GoogLeNet一样,在ResNet中加入全局平均汇聚层,以及全连接层输出。
# 每个模块有4个卷积层(不包括恒等映射的1 × 1卷积层)。加上第一个7 × 7卷积层和最后一个全连接层,共有18层。因此,这种模型通常被称为ResNet-18。
net = nn.Sequential(b1, b2, b3, b4, b5,
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(), nn.Linear(512, 10))
# 观察一下ResNet中不同模块的输入形状是如何变化的。在之前所有架构中,分辨率降低,通道数量增加,直到全局平均汇聚层聚集所有特征。
X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
X = layer(X)
print(layer.__class__.__name__,'output shape:\t', X.shape)
# 库中的函数没有取最优的准确率,自己实现一个
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
"""Train a model with a GPU (defined in Chapter 6).
Defined in :numref:`sec_lenet`"""
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
print('training on', device)
net.to(device)
optimizer = torch.optim.SGD(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss()
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
legend=['train loss', 'train acc', 'test acc'])
timer, num_batches = d2l.Timer(), len(train_iter)
best_test_acc = 0
for epoch in range(num_epochs):
# Sum of training loss, sum of training accuracy, no. of examples
metric = d2l.Accumulator(3)
net.train()
for i, (X, y) in enumerate(train_iter):
timer.start()
optimizer.zero_grad()
X, y = X.to(device), y.to(device)
y_hat = net(X)
l = loss(y_hat, y)
l.backward()
optimizer.step()
with torch.no_grad():
metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
timer.stop()
train_l = metric[0] / metric[2]
train_acc = metric[1] / metric[2]
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,
(train_l, train_acc, None))
test_acc = d2l.evaluate_accuracy_gpu(net, test_iter)
if test_acc>best_test_acc:
best_test_acc = test_acc
animator.add(epoch + 1, (None, None, test_acc))
print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
f'test acc {test_acc:.3f}, best test acc {best_test_acc:.3f}')
# 取的好像是平均准备率
print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
f'on {str(device)}')
'''训练并打印训练耗时'''
'''开始计时'''
start_time = time.time()
lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
# 使用自己的训练函数
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
'''计时结束'''
end_time = time.time()
run_time = end_time - start_time
# 将输出的秒数保留两位小数
if int(run_time)<60:
print(f'{round(run_time,2)}s')
else:
print(f'{round(run_time/60,2)}minutes')
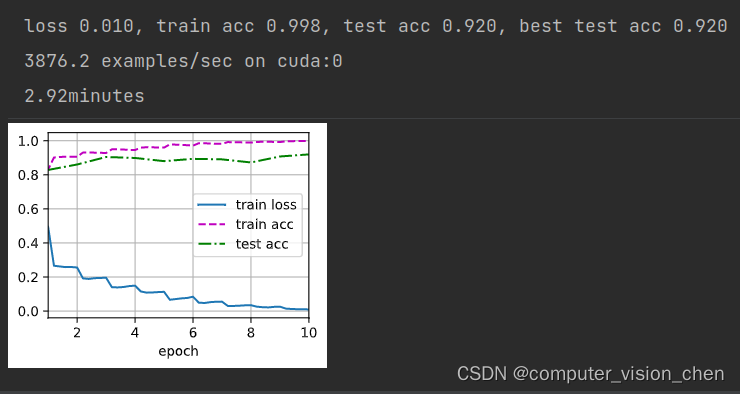
牛逼!比之前所有的模型准确率都高。
参考文章与视频
三分钟说明白ResNet ,关于它的设计、原理、推导及优点
https://www.bilibili.com/video/BV1cM4y117ob/?spm_id_from=333.337.search-card.all.click&vd_source=ebc47f36e62b223817b8e0edff181613
ResNet详解——通俗易懂版
https://blog.csdn.net/sunny_yeah_/article/details/89430124





![[oeasy]python0083_[趣味拓展]字体样式_正常_加亮_变暗_控制序列](https://img-blog.csdnimg.cn/img_convert/91faeddc16aee1cfdc71fe7dafc341fc.png)