110.平衡二叉树

力扣题目链接

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

110.平衡二叉树

返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

110.平衡二叉树1

返回 false 。

知识准备

这里要强调一些概念，什么是深度又什么是高度。

深度：根节点到叶子结点的距离
高度：叶子节点到根节点的距离

用一张图会更加直观

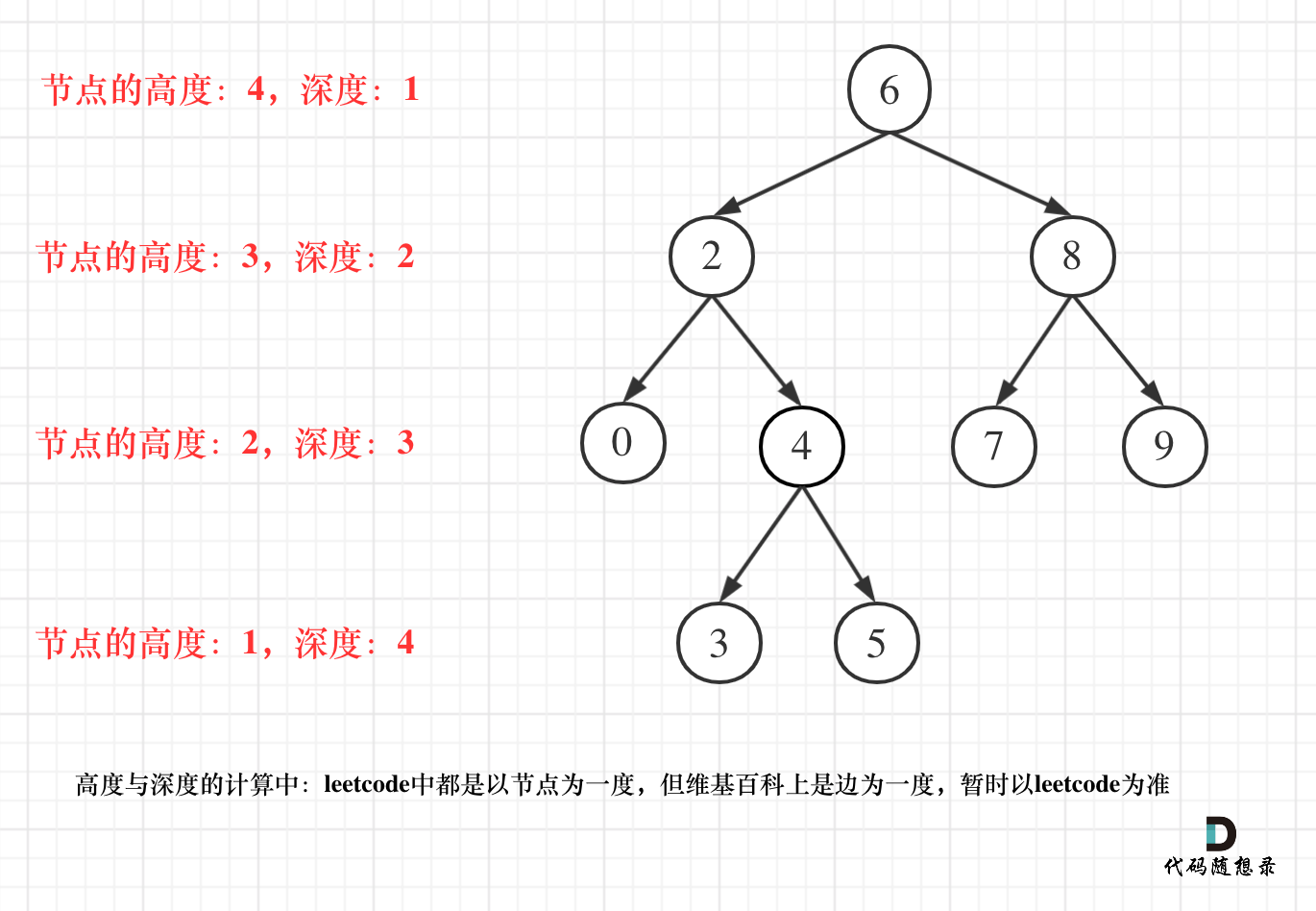
110.平衡二叉树2

对于深度和高度的求法，各有不同，求深度应该从上到下，使用前序遍历，而高度是从下到上，应该是后序遍历

在之前的求二叉树的最大深度时，使用的是后序，原因是求的是叶子节点的深度，也为根节点的高度。

如果是正经用前序遍历求深度，代码如下：

class Solution {
private:
    int res;
public:
    void getDepth(TreeNode* node, int depth){
        res = max(res,depth);
        if(node->left == nullptr && node->right == nullptr)return ;

        if(node->left){
            depth++;
            getDepth(node->left,depth);
            depth--;
        }
        if(node->right){
            depth++;
            getDepth(node->right,depth);
            depth--;
        }
        return;
    }
    int maxDepth(TreeNode* root) {
        res = 0;
        if(root == nullptr)return res;
        getDepth(root,1);
        return res;
    }
};

思路

首先确定我们要求的应该是高度，使用后序遍历。

确定终止条件

if(root == null)return 0

返回0则是高度为0

单层循环

确定终止条件后，分别求左右子树的高度。

		int leftHeight = getHeight(root->left);
        if(leftHeight == -1)return -1;
        int rightHeight = getHeight(root->right);
        if(rightHeight == -1)return -1;

确定高度差

		int res = 0;
        res = abs(leftHeight-rightHeight) > 1?-1:1+max(leftHeight,rightHeight);
        return res;

最终代码如下：

class Solution {
public:
    int getHeight(TreeNode* root){
        if(root == nullptr)return 0;
        
        int leftHeight = getHeight(root->left);
        if(leftHeight == -1)return -1;
        int rightHeight = getHeight(root->right);
        if(rightHeight == -1)return -1;

        int res = 0;
        res = abs(leftHeight-rightHeight) > 1?-1:1+max(leftHeight,rightHeight);
        return res;
    }
    bool isBalanced(TreeNode* root) {
        return getHeight(root) == -1?false:true;
    }
};