算法套路二十——单调栈

单调栈是一种特殊的数据结构，用于解决与元素的相对大小有关的问题。它是一个栈，但其中的元素以单调递增或单调递减的顺序排列，用于处理与相对大小有关的问题。

算法示例：下一个更大元素

给定一个数组 nums ，返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

单调栈（Monotonic Stack）是一种特殊的数据结构，用于解决一类与寻找下一个更大/更小元素有关的问题。它的特点是栈内的元素保持严格的单调性，可以是递增减。具体步骤如下

1. 初始化一个空栈。
2. 遍历数组或列表中的每个元素。
3. 对于每个元素，执行以下操作：
   • 如果栈为空，则当前元素入栈。
   • 如果当前元素小于等于栈顶元素，当前元素入栈。
   • 如果当前元素大于栈顶元素，则说明当前元素是栈顶元素的下一个更大（更小）元素：
     • 不断地弹出栈顶元素，并记录栈顶元素的下一个更大（更小）元素为当前元素。
     • 将当前元素入栈。
4. 继续处理步骤3，直到遍历完成。
5. 如果栈中还有元素，说明它们没有下一个更大（更小）元素，默认为 -1 或者其他特定值。

通过使用单调栈，我们可以在线性扫描中高效地解决这类问题，而不需要套循环。这是因为栈保持了部分信息的记录，我们可以在遍历每个元素时快速找到相关的下一个更大（更小）元素或者距离。

func nextGreaterElement(nums []int) []int {
    n := len(nums)
    ans := make([]int, n)
    stack := []int{}
    for i := n - 1; i >= 0; i-- {
        num := nums[i]  
        // 注意是大于等于
        for len(stack) > 0 && num >= stack[len(stack)-1] {
            stack = stack[:len(stack)-1] // 栈顶元素出栈
        }
        if len(stack) > 0 {
            ans[i] = stack[len(stack)-1]
        } else {
            ans[i] = -1
        }
        stack = append(stack, num)
    }    
    return ans
}

算法练习一：LeetCode503. 下一个更大元素 II

func nextGreaterElements(nums []int) []int {
    n := len(nums)
    ans := make([]int, n)
    stack := []int{}
    // 从后往前遍历数组的两倍长度
    for i := 2*n - 1; i >= 0; i-- {
        num := nums[i % n]  
        // 注意是大于等于，因为复制了数组，所以出现相等时也需要将栈顶元素出栈
        for len(stack) > 0 && num >= stack[len(stack)-1] {
            stack = stack[:len(stack)-1] // 栈顶元素出栈
        }
        if len(stack) > 0 {
            ans[i%n] = stack[len(stack)-1]
        } else {
            ans[i%n] = -1
        }
        stack = append(stack, num)
    }    
    return ans
}

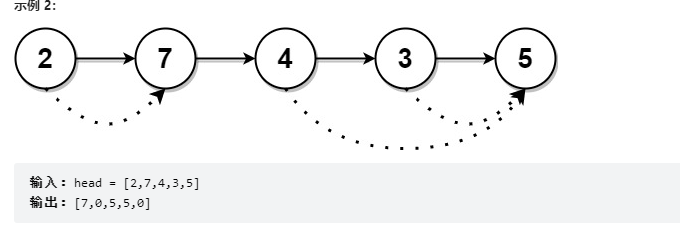
算法练习：LeetCode1019. 链表中的下一个更大节点

func nextLargerNodes(head *ListNode) []int {
    type pair struct{x,i int}
    st:=[]pair{}
    ans:=[]int{}

    for cur:=head;cur!=nil;cur=cur.Next{
        ans=append(ans,0)
        for len(st) > 0 &&cur.Val>st[len(st)-1].x{
            ans[st[len(st)-1].i]=cur.Val
            st=st[:len(st)-1]
        }
        st=append(st,pair{cur.Val,len(ans)-1})

    }
    return ans
}

算法进阶一：LeetCode496. 下一个更大元素 I

哈希表+单调栈+倒序遍历

本题有一个难点就是如何找到num1在nums2中的对应位置，因此我们可以改变思路。
由于nums1是nums2的子集且nums2不重复，可以首先构建一个哈希表mp，首先利用底大顶小的单调栈预处理 nums2，倒序遍历nums2（倒序遍历可以不用记录num的下标），来记录num2中每个元素的右侧下一个更大元素，这样我们可以避免每次遍历 nums1 中的元素时都遍历其在nums2中的位置。具体步骤如下

1. 哈希表 mp记录num2中元素的下一个更大值，单调栈 stack底大顶小，对于每个元素 num，如果 num大于栈顶的元素，那么栈顶的元素就不可能是 num 的下一个更大元素，因此从栈顶开始弹出所有小于 num 的元素，以保持栈中的元素单调递减。只有比栈顶小的元素才能入栈。
2. 倒序遍历 nums2：
   • 弹出栈中所有小于当前元素的元素。
   • 如果栈不为空，则将栈顶元素存入映射表 mp，表示当前元素的右边第一个更大元素。
   • 如果栈为空，则将 -1 存入映射表 mp，表示当前元素没有右边的更大元素。
   • 将当前元素压入栈中。
3. 遍历 nums1，对于每个元素 num：
   • 从映射表 mp 中查找 num 对应的右边第一个更大的元素，并将其存入 res 中。

func nextGreaterElement(nums1, nums2 []int) []int {
    mp := map[int]int{}  // 创建一个空的映射表，用于存储元素和其下一个更大元素的对应关系
    stack := []int{}  // 创建一个空的栈，用于辅助查找下一个更大元素
    for i := len(nums2) - 1; i >= 0; i-- {  // 从nums2的最后一个元素开始遍历
        num := nums2[i]
        for len(stack) > 0 && num >= stack[len(stack)-1] {  // 当栈不为空且当前元素大于等于栈顶元素时
            stack = stack[:len(stack)-1]  // 从栈中弹出栈顶元素，直到栈为空或当前元素小于栈顶元素
        }
        if len(stack) > 0 {
            mp[num] = stack[len(stack)-1]  // 将当前元素所对应的下一个更大元素存入映射表中
        } else {
            mp[num] = -1  // 如果栈为空，则当前元素没有下一个更大元素，将映射表的值设为-1
        }
        stack = append(stack, num)  // 将当前元素压入栈中
    }
    res := make([]int ,len(nums1))  // 创建与nums1相同长度的结果切片
    for i, num := range nums1 {
        res[i] = mp[num]  // 根据映射表找到nums1中每个元素的下一个更大元素并存入结果切片中
    }
    return res  // 返回结果切片
}