摘要

知识图推理旨在从已有的知识中推断出新的事实。基于关系路径的方法在文献中显示出较强的可解释性和归纳推理能力。然而，在KG中 捕获复杂拓扑(Capturing complex topology) 时，路径是有限的。本文引入了一种新的关系结构，即 由重叠关系路径组成的关系有向图（r-digraph） 来捕获KG的结构信息。由于有向图表现出比路径更复杂的结构，因此在r-digraph上构建和学习是具有挑战性的。在这里，我们提出了一种图神经网络，即RED-GNN，通过使用GNN的变体学习关系有向图来解决上述挑战。明确地RED-GNN递归编码多个具有共享边的r-digraph，并通过依赖于查询的注意力权重来选择强相关边。我们展示了在用看不见的实体推理KG和通过r-digraph完成KG基准、RED-GNN的效率以及在r-digraph可解释的依赖性方面的显著收获。

知识图谱中实体和概念通过关系连接在一起。拓扑结构是指这些连接关系的模式和形式。
在知识图谱中，有时候实体之间的关系非常复杂，涉及多个层次和路径。"Capturing complex topology"的目标是能够准确地表示和捕捉这些复杂的连接关系。这可以包括以下方面：
1.多层级关系：有些关系可能涉及多个层级，例如，实体A与实体B通过实体C相连，而实体C又与实体D相连。在捕捉复杂拓扑结构时，需要能够表示和处理这种多层级的关系。
2.循环关系：有时候在知识图谱中存在循环关系，也就是实体之间存在循环的连接路径。例如，实体A通过关系R1与实体B相连，而实体B又通过关系R2与实体A相连。在建模复杂拓扑结构时，需要能够处理这种循环关系。
3.多路径连接：有时候两个实体之间可以通过多个不同的路径相连。例如，实体A通过关系R1和关系R2分别与实体B相连。在捕捉复杂拓扑结构时，需要能够同时表示和利用多个路径。
为了实现对复杂拓扑结构的捕捉，可以使用图神经网络（Graph Neural Networks）等技术。

在知识图谱中，实体之间的关系可以通过多个路径进行连接。有时候这些路径之间可能存在交叉或重叠的情况，即多个路径共享相同的一部分关系。为了更好地表示和理解这种情况，可以使用由重叠关系路径组成的关系有向图。
在这个有向图中，节点表示实体，有向边表示关系，而路径则由多个有向边组成。当多个路径共享相同的一部分关系时，可以通过在有向图中创建重叠边来表示这种情况。重叠边表示两个不同的路径之间的关系重叠或交叉。
假设我们有一个知识图谱，其中包含以下实体和关系：
实体：A、B、C、D、E
关系：R1、R2、R3
现在我们来构建由重叠关系路径组成的关系有向图。
假设存在以下路径：
路径1: A → R1 → B → R2 → C
路径2: A → R3 → D → R2 → C
路径3: E → R1 → B → R2 → C
在这个关系有向图中，节点表示实体，有向边表示关系，而路径则由多个有向边组成。我们可以看到，路径1和路径2共享关系R2，而路径1和路径3共享关系R1
这个关系有向图可以帮助我们更好地理解实体之间的连接关系。例如，通过观察有向图，我们可以发现实体A和实体C之间存在两条不同路径，分别通过关系R1和关系R3。这可能暗示了A和C之间的某种关联或相似性。
通过分析这个由重叠关系路径组成的关系有向图，我们可以进行路径相似性计算、关联规则挖掘等任务。例如，我们可以计算路径1和路径2之间的相似性，或者挖掘出实体之间的关联规则，如"A → R1 → B → R2 → C" implies “A → R3 → D → R2 → C”。

介绍

真实世界的KG很大，而且高度不完整，因此推断新的事实是具有挑战性的。KG推理模拟了从现有事实推断出新的事实的过程。在本文中，我们重点学习关系结构，用于以（主体-实体，关系，？）。

在过去的十年里，基于三元组模型的知识学习在KG中得到了很大的关注。这些模型直接推理具有实体和关系嵌入的三元组，但由于三元组是独立学习的，它们不能明确地捕获结构信息，即查询三元组周围的局部结构，这些结构可以用作KG推理的证据。

关系路径第一次尝试捕获用于推理的结构信息。使用强化学习（RL）对与查询 具有强相关性的关系路径进行采样。由于KG的稀疏特性，RL方法很难在大规模KG上训练。PathCon对实体之间的所有关系路径进行采样，并使用注意力机制对不同路径进行加权。但是对于实体查询任务来说是昂贵的。基于规则的方，将关系路径概括为逻辑规则，学习通过关系的逻辑组成，并可以提供可解释的见解。此外，逻辑规则可以传输到以前看不见的实体，这些实体在现实世界的应用程序中很常见，而基于三元组的模型无法处理这些实体。

在获取结构信息方面，子图自然比路径信息更丰富。随着图神经网络（GNN）在图结构数据建模方面的成功。GNN已被引入来捕获KG中的子图结构。R-GCN和CompGCN提出通过聚合每层KG上的所有1跳邻居来更新实体的表示。然而，它无法区分不同邻居的结构依赖性，也无法解释。DPMPN通过保留给定查询的最可能实体，而不是学习特定的局部结构，学会了在大规模KGs上减少推理子图的大小。最近，GraIL提出了从局部封闭子图结构预测关系，并展示了子图的归纳能力。然而它由于封闭子图的限制，也面临有效性和效率问题。

受基于路径的方法的可解释性和可转换性以及子图的结构保持性的启发，我们在KG中引入了一种新的关系结构，称为r-digraph。r-digraph通过保留重叠的关系路径和关系的结构来进行推理，从而将关系路径推广到子图。与结构简单的关系路径不同，如何有效地构建和学习r-digraph是一项挑战，因为直接在每个r-digraph上进行计算对于推理查询来说是非常昂贵的。受使用动态规划解决重叠子问题中计算成本的启发，我们提出了RED-GNN，这是一种具有GNN变体的关系有向图的有效学习框架。经验上，RED-GNN在具有看不见实体和不完整KG的KG的基准测试中都比最先进的推理方法显示出显著的优势。此外，训练和推理过程是有效的，学习的结构是可解释的。

相关工作

一个知识图谱形式为：K={V,R,F}，其中V,R,F={(e_s,r,e_o)|e_s,e_o∈V，r∈R}分别是一组实体、关系和三元组事实。让e_q作为查询实体，r_q作为查询关系，e_a作为答案实体。给出一个查询（e_q，r_q，？），推理任务是预测答案实体e_a。通常，V中的所有实体都是e_a的候选实体。

KG推理的关键是捕获查询周围的局部证据，如关系路径或子图。在这一部分中，我们介绍了利用$F$中的结构进行推理的基于路径的方法和基于GCN的方法。

基于路径的方法

关系路径由一组按顺序连接的三元组组成，它比单个三元组更具有信息性，因为它可以提供可解释的结果并转移至未知实体（transfer to unseen entities）。

"transfer to unseen entities"转移至未知实体
是指将知识从已知实体转移到未知实体的过程。
当我们谈论将知识转移到未知实体时，意味着在知识图谱中没有直接表示或记录的实体。这可以发生在以下情况下：
1.新实体：当一个新的实体出现，而它在知识图谱中没有相关的记录时，我们需要将知识从已知实体迁移到这个新实体上。这可以通过使用已有的关系和属性信息进行推理或利用相似实体的知识进行迁移。
2.未见实体：在某些情况下，我们可能只能观察到实体的部分信息，而无法完全了解它。这些实体被称为未见实体。在这种情况下，我们可以通过与已知实体的关系和属性进行推理，来推断并转移知识到未见实体上。

关系路径：
长度为L的关系路径是一组L个连续三元组（e₀，r₁，e₁），（e₁，r₂，e₂），… ，（e_L-1，r_L，e_L），它们按顺序首尾相连。

基于路径的方法学习通过一组关系路径作为局部证据来预测三元组(e_q, r_q, e_a)。DeepPath通过强化学习（RL）学习生成从e_q到e_a的关系路径。为了提高效率，MINERVA和M-walk通过RL来学习来自e_q的多条路径。分数由不同e_a的到达频率表示。由于KG的复杂结构，奖励非常稀疏，使得训练RL模型变得困难。PathCon对连接两个实体的所有路径进行采样，以预测它们之间的关系，这对于推理任务(e_q, r_q, e_a)来说是昂贵的。

除了直接使用路径，基于规则的方法将逻辑规则学习为关系路径的广义形式。逻辑规则是由一组关系组成的，用来推断特定的关系，以提供更好的解释，并可以传递给看不见的实体。规则可以通过离散挖掘、EM算法（如RNNLogic）或端到端训练（如Neural LP和DRUM）来学习，生成e_q和e_a之间高度相关的关系路径。规则可以提供逻辑解释并转移到看不见的实体。然而，规则只能捕获顺序证据，因此无法学习更复杂的模式，如子图结构。

基于GNN的方法

子图可以自然地保留比相对路径更丰富的信息。所有的关系路径都是从一些局部子图中采样的。因此，它们自然会丢失KG中的一些结构信息，例如多个实体和边是如何连接的。GNN在对图形结构化数据11进行建模方面具有强大的能力。这启发了最近的工作将GNN扩展到KG上，以将实体和关系在消息传递框架下的表示聚合为：

其在具有维度d的实体e_o的1跳相邻边缘（e_s，r，e_o）上的消息上聚合。Φ(·,·)是消息函数，是加权矩阵，$\delta$是激活函数。
在L层之后，捕捉实体e∈V的局部结构的表示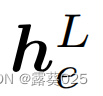与评分函数联合工作，以对三元组进行评分。由于聚合函数聚合了所有邻居的信息，并且与查询无关，因此R-GCN和CompGCN无法捕获用于推理特定查询的显式结构，并且是不可解释的。

DPMPN没有使用所有邻域，而是设计了一个GNN来聚合实体的嵌入，另一个GNN来动态扩展和修剪来自查询实体的推理子图，例如•在采样实体上应用与查询相关的注意力进行修剪。这种方法通过关注修剪后的子图来展示可解释的推理过程，但仍然需要嵌入来指导修剪，因此不能推广到看不见的实体。此外，它不能捕获支持给定查询三元组的显式子图结构。xERTR LIOJ扩展了用于推理时态KGs中未来三元组的DPMPN。

最近，GralL提出提取查询实体e_q和回答实体e_a之间的封闭子图G(e_q,e_a)。为了学习封闭子图，在G(e_q,e_a)中，在边上应用具有查询相关注意力的关系GNN，以控制边对不同查询的重要性。在L层的聚合之后，聚合子图中所有实体e∈V的图级表示用于对三元组（e_q，r_q，e_a）进行评分。由于需要显式地提取子图并对不同的三元组进行评分，因此计算成本非常高。

关系有向图

关系路径，尤其是逻辑规则，在KG上显示出强大的推理能力，可以提供可解释的结果并转移到看不见的实体。然而，由于它们是从局部子图中采样的，因此在KG中捕获更复杂的依赖关系时，它们是有限的。基于GNN的方法可以学习不同的子图结构。但现有的方法都无法有效地学习子图结构，这些子图结构既可解释又可转移到规则等看不见的实体。因此，我们有动机定义一种新的结构，即r-digraph，通过推广关系路径来探索结构依赖性。在下一节中，我们展示如何定制GNN可以有效地从r-digraph中学习。
分层ST图：
分层st图是一个有向图，只有一个源节点（s）和一个 汇节点（t） 。所有的边都是有向的，连接连续层之间的节点，并从较低层指向较高层。

汇节点是指一个节点，它只接收来自其他节点的边，而不发出任何边。换句话说，它是一个只有入度没有出度的节点。

在这里，我们采用一般的方法来增强具有反向和同一关系的三元组。那么在e_q和e_a之间长度小于或等于L的所有关系路径都可以表示为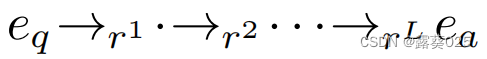长度为L。这样，它们可以形成为分层st图中的路径，具有单个源实体e_q和单个汇点实体e_a。这样的结构保留了e_q和e_a之间长度为L的所有关系路径，并保持了子图结构。

r-digraph：
r-digraph 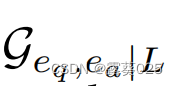是一个具有源实体e_q和汇实体e_a的分层st图。同一层中的实体彼此不同：r-digraph中从e_q指向e_a的任何路径都是长度为L的关系路径 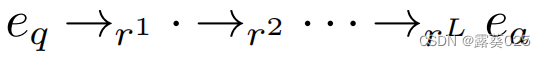，其中$r^l$连接$l-1$层中和$l$层中的实体。如果没有连接e_q和e_a的关系路径我们定义为。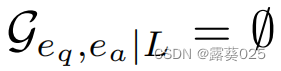

上图中的（b）提供了一个r-digraph的例子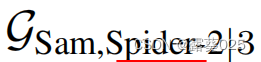，使用了新的三元组（Sam，directed，Spider-2），如图（a）所示。受关系路径推理能力的启发，我们的目的是利用r-digraph进行KG推理。然而，与结构简单的关系路径不同，如何有效构建和学习r-digraph是具有挑战性的。

RED-GCN

要对r-digraph进行编码，一个简单的解决方案首先是构造它，并使用公式1和下列算法运行消息。对于构造，我们在步骤2和4中获得e_q的外边缘和实体。如果，为空，那么我们在步骤5中将表示设置为0。对于不为空的，我们在步骤6-8中将其从e_a向后构造。构造完成后，我们在第10步逐层在上运行消息传递。由于e_a是的单汇实体，因此最终的层表示用作子图表示，以对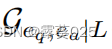的结构进行编码。

然而，上述算法1非常昂贵。首先给出一个查询（e_q，r_q，？），我们需要对有不同答案实体e_a∈V的不同的三元组|V|执行这个算法。其次，在这个算法中需要三个回路。需要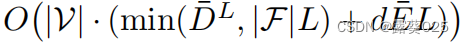来预测给定的查询（e_q，r_q，？），其中D是V中实体的平均得分，E是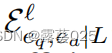中边的平均分数。为了提高有效性，我们提出了递归编码对个r-digraph。

r-digraph递归编码

在算法1中，当对相同查询（e_q，r_q，？）枚举不同的e_a∈V（e_q，r_q，e_a）时候，e_q的邻边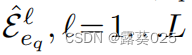就被共享了。因此，有了以下的观察：
$l$步骤中来自e_q的一组可见边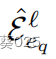是在r-digraph中在e_q和所有实体e_a∈V的第$l$层边的集合，即。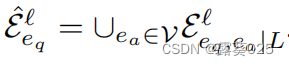

上述指出，第$l$层不同实体e_a的边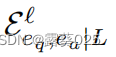共享同一组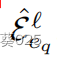的边 。受使用动态规划在重叠子问题中节省计算成本的启发，e_q和任何实体e_o之间的r-digraph可以递归地构造为

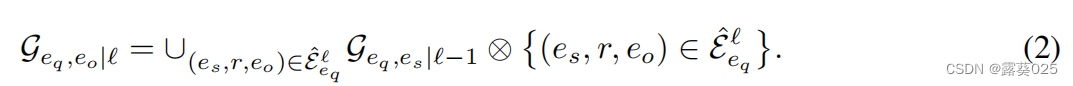
基于上述，我们的动机是用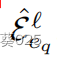的共享边逐层递归地对多个r-digraph进行编码。过程如下

给出一个相同三元组（e_q，r_q，e_a），通过算法1和算法2在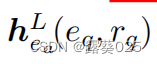上构建编码完全相同。

学习用于查询的基本信息

至此，查询关系r_q的信息还没有得到处理。为了学习r-digraph的查询相关表示，我们将聚合函数指定为：

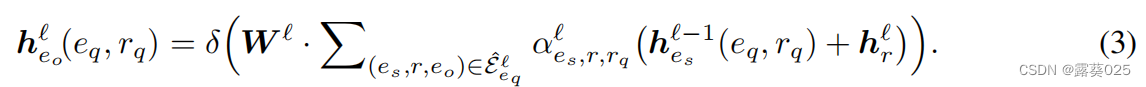
为了发现重要的边，特别是关系，在每一层，r_q被编码到注意力权重为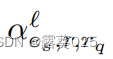的每一条边上：

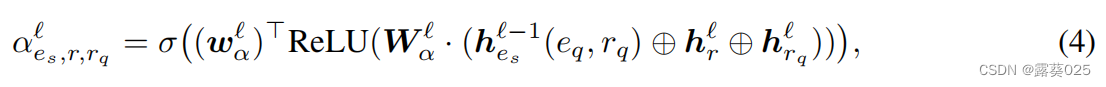
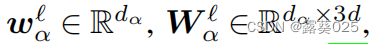
在这之后，L层的聚合（3），可以编码用于评分的基本信息。因此我们设计了一个简单的评分函数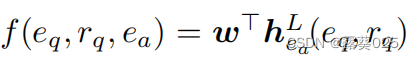：，。我们将多类损失函数与每个训练三元组（e_q，r_q，e_a）关联起来，即：

实验