版权声明

原创作品，整理不易，转载请标明出处。本篇推送更详细的内容介绍，可参见本人微信公众号“优化与博弈的数学原理”，公众号二维码参见文末。

编者按

OFDM系统中的功率分配问题是通信领域中的研究热点。本文重点考虑了面向同频干扰场景下OFDM系统的功率分配问题，该问题通常被建模为含复杂多耦合变量的非凸优化问题，因此现有方法难以求得该问题的最优解（即存在对偶间隙）。本篇推送通过文献阅读及相关调研，学习并记录了基于 Time-Sharing Condition 及 General Duality Theory 的求解思路，该方法可有效解决同频干扰场景下OFDM系统功率分配问题的非凸性，相关文献证明了在特定的条件下，该方法可以完全消除对偶间隙。

一、问题描述

问题1：无干扰场景下的信道容量最大化

先让我们回顾一下MIMO无线通信领域的一个常见问题，受限功率下最大化信道容量问题，即注水问题：
$$\begin{array}{rl}{P}_1:& {\min }_p\sum _{n=1}^{N}log(1+\frac{p_n}{{\sigma }_n^2})\\ & s.t.\{\begin{array}{l}p⪰0\\ \sum _{n=1}^N{p}_n\le P\end{array}\end{array}$$

其中，目标函数表示包含 $N$ 个并行子信道的系统信道容量（如OFDM系统）。$p=\left[p_1,p_2,\dots ,p_N\right]$ 表示信号功率且为决策变量， $p_n$是子信道$n$中的信号功率，${\sigma }_n^2$是子信道$n$中的噪声功率。

问题2：有干扰场景下的信道容量最大化

今天主要想介绍，在存在干扰的情况下，如何求解其优化问题，并确保对偶间隙为0。 仍然考虑K个用户，N个子信道的优化问题，如下：
$$\begin{array}{rl}{P}_2:& {\min }_p\sum _{k=1}^K{w}_k\sum _{n=1}^{N}log(1+\frac{p_k^n}{{\sigma }_k^n+{\sum }_{j\ne k}{\alpha }_{jk}^n{p}_j^n)}\\ & s.t.\{\begin{array}{l}{p}_k^n\ge 0,\forall k,n\\ \sum _{n=1}^N{p}_n^k\le P_k,\forall k\end{array}\end{array}$$
注1：上述问题摘自 Multiuser DSLs 场景，与 OFDM 类似，后文不予区分 DSL 与 OFDM 的区别；
注2：为方便符号表述，${\sigma }_k^n$表示噪声功率，这里不写平方了。

下文，我们将回顾问题1的经典求解方法[1]，并详细介绍针对问题2的研究现状、理论证明及求解方法。

二、问题1的求解方法（基础回顾）

由于问题1满足 Slater 条件，故具有强对偶性，且其 Lagrange 函数为：

$$L(p,\lambda ,\nu )=-\sum _{n=1}^{N}log(1+\frac{p_n}{{\sigma }_n^2})-{\lambda }^{T}p+\nu (\sum _{n=1}^N{p}_n-P)$$
计算其KKT条件：
$$\frac{\partial L(p,\lambda ,\nu )}{\partial p_n}=\frac{-1}{1+\frac{p_n}{{\sigma }_n^2}}\frac{1}{{\sigma }_n^2}-{\lambda }_n+\nu =0$$
可得：
$${\lambda }_n=\nu -\frac{1}{p_n+{\sigma }_n^2}$$

• 情况1：${\lambda }_n>0$ 且 $p_n=0$ ⇒ ${\lambda }_n=\nu -\frac{1}{{\sigma }_n^2}>0$ ⇒ $\frac{1}{\nu }<{\sigma }_n^2$
• 情况2：${\lambda }_n=0$ 且 $p_n\ge 0$ ⇒ $\nu =\frac{1}{p_n+{\sigma }_n^2}$ ⇒ $p_n=\frac{1}{\nu }-{\sigma }_n^2\ge 0$

因此：
p n ∗ = max ⁡ { 0 , 1 ν ∗ − σ n 2 } p_n^*=\max\{0,\frac{1}{\nu^*}-\sigma_n^2\} pn∗​=max{0,ν∗1​−σn2​}

其中，最优解 $\frac{1}{{\nu }^{\ast }}$ 可由下式解出：【记下式为$(\ast )$式】
∑ n = 1 n p n ∗ = max ⁡ { 0 , 1 ν ∗ − σ n 2 } = P \sum\limits_{n=1}^n p_n^* = \max\{0,\frac{1}{\nu^*}-\sigma_n^2\}=P n=1∑n​pn∗​=max{0,ν∗1​−σn2​}=P

显然求和约束在最优解处一定为紧约束，故取等。现求解 $(\ast )$ 式的方法如下：

首先，假设对任意 $n$ 都有 $p_n>0$（即对任意 $n$ 都有$\frac{1}{\nu }-{\sigma }_n^2>0$），然后找到$(\ast )$式的解 $\frac{1}{{\nu }^{\ast }}$。若不存在可行解，则可得 $p_l^{\ast }=0$，其中 l = a r g m a x { σ n 2 } l=argmax\{\sigma_n^2\} l=argmax{σn2​}，再次求解 $(\ast )$ 式得到 $\frac{1}{{\nu }^{\ast }}$ 。重复上述步骤，使得每次循环的时候，在剩余子信道中至少有一个子信道（对应于噪声功率最大的子信道）的功率为0，直到获得最优的 $\frac{1}{{\nu }^{\ast }}$ 与 $p_n^{\ast }>0$ 为止。上述方法获得的解称作集中式解，记作向量 $p^{\ast }$ 。这个解也是 ${\lambda }_1=\cdots ={\lambda }_N$ 时， $(\ast )$ 式的最优解；也是凸矢量优化问题式 $(\ast )$ 的 Pareto 最优解，其在 Pareto 边界上的目标函数值为：

$$(R_1^{\ast }=log(1+\frac{p_1^{\ast }}{{\sigma }_1^2},\dots ,R_n^{\ast }=log(1+\frac{p_N^{\ast }}{{\sigma }_N^2}))$$

上述思想的核心原理如下图所示：

三、问题2的研究现状（文献综述）

现状 1 ：

Iterative waterfilling (迭代注水，后文简称 IWF) [2] 是早期的多用户频谱优化技术之一，它利用DSL调制解调器进行频谱整形。在IWF算法中，每个用户通过执行单用户注水，将来自所有其他用户的串扰干扰视为噪声，迭代地最大化自己的可实现速率。但是，IWF进程并不寻求为整个DSL包找到全局最优。该方法只是将每个用户都看成一个非合作博弈的参与者，最终IWF会收敛至一个均衡点。虽然IWF不是最优的，但该方法已被证明优于传统的SSM方案。
解释：
这里以OFDM为例，解释一下上述加粗字体的含义。首先，信道容量可计算为：$C=log(1+\frac{P}{N})$，其中 $P$ 是信号功率，$N$ 是噪声功率。如果总信号功率被拆为两部分，即：$P=P_1+P_2$，则可以验证以下公式：

$$\begin{array}{rl}C& =log(1+\frac{P_1+P_2}{N})=log((1+\frac{P_1}{N})+\frac{P_2}{N})\\ & =log\left[(1+\frac{P_1}{N})(1+\frac{P_2}{P_1+N})\right]\\ & =log(1+\frac{P_1}{N})+log(1+\frac{P_2}{P_1+N})\end{array}$$
也就是说，在这两部分功率中，第一份功率 $P_1$ 产生了一个容量 $log(1+\frac{P_1}{N})$ ，功率 $P_1$ 同时等效成了对第二份功率的噪声。了解了这个原理，不难读懂 IWF 算法中，“每个用户通过执行单用户注水，将来自所有其他用户的串扰干扰视为噪声，迭代地最大化自己的可实现速率”的原理及算法思想了。

现状 2 ：

[3]提出精确OSB算法，可实现全局最优解，该方法的基本策略是将信道容量优化问题 $P_2$ 转化为对偶域，转换成拉格朗日对偶的形式：

$$\begin{array}{rl}{P}_3:& {\min }_p\sum _{k=1}^K{w}_k\sum _{n=1}^{N}log(1+\frac{p_k^n}{{\sigma }_k^n+{\sum }_{j\ne k}{\alpha }_{jk}^n{p}_j^n)}+\sum _{k=1}^K{\lambda }_k(P_k-\sum _{n=1}^N{p}_n)\\ & s.t.p_k^n\ge 0,\forall k\end{array}$$

该文献的核心思想是为每个非负且固定的 $({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_K)$ 集合，分别求解其拉格朗日函数。然后，原优化问题 $P_2$ 的解，可在 $\lambda$ 空间内，通过嵌套式的二分法搜索找到。可以看出，OSB算法的计算复杂度与载波数 $N$ 呈线性关系。如[3]所示，与IWF相比，OSB算法可以提供显著的性能改进。
OSB算法的缺点：OSB算法的计算复杂度虽然对载波数 $N$ 是线性的，但在用户数量 $K$ 上仍然是指数级的。即：OSB算法的复杂性变得令人望而却步。

四、问题2的求解方法（优化理论）

在本节我将先后介绍时域共享条件（Time-Sharing Condition）及其证明[4]，随后说明有干扰场景下的信道容量最大化问题 $P_2$ 满足 Time-Sharing Condition。

PART I ： Time-Sharing Condition

在多载波系统中，优化目标和约束通常由大量单独的函数组成，每个函数对应于一个频率载波。因此，优化问题具有以下一般形式：【记下式为 $(\ast \ast )$ 式】
$$\begin{array}{rl}{P}_4:& {\max }_p\sum _{n=1}^N{f}_n(x_n)\\ & s.t.\sum _{n=1}^N{h}_n(x_n)\le P\end{array}$$
其中，$x_n\in {\mathcal{R}}^K$ 为优化问题中的决策变量，函数 $f_n(x):{\mathcal{R}}^K\to \mathcal{R}$ 不必是凹函数，函数 $h_n(x):{\mathcal{R}}^K\to {\mathcal{R}}^K$ 也不必是凸函数。功率约束以 $K$ 维向量 $P$ 表示，即：component-wise inequality。

上述的泛化优化问题， 在考虑 $N$ 个子载波、$K$ 个用户的场景下，对应在多用户 OFDM 系统中有下述结论：

$$\begin{array}{r}\{\begin{array}{l}{x}_n=(p_1^n,p_2^n,\dots ,p_K^n)\in {\mathcal{R}}^K\\ f_n(x_n)={\sum }_{k=1}^K{w}_{k}log(1+\frac{p_k^n}{{\sigma }_k^n+{\sum }_{j\ne k}{\alpha }_{jk}^n{p}_j^n})\\ h_n(x_n)={\left[p_1^n,p_2^n,\dots ,p_K^n\right]}^T\end{array}\end{array}$$

下面考虑 $(\ast \ast )$ 式的对偶问题，先求其 Lagrangian 函数：

$$L(x_n,\lambda )=\sum _{n=1}^N{f}_n(x_n)+{\lambda }^T(P-\sum _{n=1}^N{h}_n(x_n))$$

定义对偶目标函数 $g(\lambda )$ 如下：

$$g(\lambda )=\max L(x_n,\lambda )$$

则对偶优化问题为：
$$\begin{array}{rl}{P}_5:& {\min }_{\lambda }g(\lambda )\\ & s.t.\lambda \ge 0\end{array}$$

显然，当 $f_n(x_n)$ 是凹函数且 $h_n(x_n)$ 是凸函数时，标准凸优化结果保证了原问题 $P_4$ 与对偶问题 $P_5$ 具有相同的解，此时对偶间隙为0。而当 $f_n(x_n)$ 不是凹函数或 $h_n(x_n)$ 不是凸函数时，对偶问题提供了一个解，该解是 $P_5$ 的上界，此时对偶间隙未必是0。这是教材告诉我们的。**而本节的主要目的，是给出即使优化问题不是凸问题，对偶间隙也为零的条件。**为此，定义了以下 Time-Sharing Condition：

定义：
令 $x_n^{\ast }$ 与 $y_n^{\ast }$ 分别是在给定 $P=P_x$ 与给定 $P=P_y$ 条件下，优化问题 $P_4$ 的最优解。如果对任意的 $P_x$ 与 $P_y$ ，对任意的 $0\le \nu \le 1$ ，都存在一个可行的 $z_n$ ，使得下式成立：
$$\begin{array}{r}\{\begin{array}{l}\sum _{n=1}^N{h}_n(z_n)\le \nu P_x+(1-\nu )P_y\\ \sum _{n=1}^N{f}_n(z_n)\ge \nu \sum _{n=1}^N{f}_n(x_n^{\ast })+(1-\nu )\sum _{n=1}^N{f}_n(y_n^{\ast })\end{array}\end{array}$$
则称优化问题 $P_4$ 满足 Time-Sharing Condition。

理解：
上述定义看起来很玄幻，但其本质并不难理解。首先，要知道原始优化问题 的最优解（optimal solutions）是 $x_n^{\ast }$，很显然 $x_n^{\ast }$ 必须满足约束 $\sum _{n=1}^N{h}_n(x_n^{\ast })=P$ 为紧约束。因此，约束上限 $P$ 的取值，决定了 $x_n^{\ast }$ 的取值。所以，我们也可以将 $x_n^{\ast }$ 看成 $P$ 的函数，即：$x_n^{\ast }=x_n^{\ast }(P)$ 。其次，理解了这一点，就可以理解为什么定义中要给定 $P=P_x$ 与 $P=P_y$ 这两种情况了，其实就是为了刻画 $x_n^{\ast }=x_n^{\ast }(P_x)$ 以及 $y_n^{\ast }=y_n^{\ast }(P_y)$ ，通过变化不同的 $P$ 值（体现在定义中“对任意的 $P=P_x$ 与 $P=P_y$ ”一句），研究函数的性质。最后，需要理解作者为什么要这么刻画呢？其实就是为了说明函数整体的凹凸性而已。观察第一条约束描述的是对整体约束函数 $\sum _{n=1}^N{h}_n(x_n)$ 凸性的刻画（注意，刻画的不是单独的 $h_n(x_n)$ 函数，没必要研究单独的一个 $h_n(x_n)$ 函数是否为凸性）；观察第二条约束描述的是整体目标函数 $\sum _{n=1}^N{f}_n(x_n)$ 凹性的刻画。

因此，可以理解 Time-Sharing Condition 无非是通过刻画求和后，函数整体的凹凸性，以替代单独每一个函数凹凸性。显然，如果每一个函数的凹凸性得到满足，那么 Time-Sharing Condition 自然成立，因此这部分理论也被称为广义对偶理论（General Duality Theory）。

PART II ： 定理及其证明

接下来介绍 Time-Sharing Condition 有什么作用？主要体现在下述定理：

定理：
考虑如 所示的优化问题形式，如果满足 Time-Sharing Condition，则该优化问题的对偶间隙为0。

证明：

显然，如果 $h_n(x_n)$ 是凸函数、$f_n(x_n)$ 是凹函数，根据保凸运算易知，优化问题是凸优化问题，则其对偶间隙为0。下面我们证明：当 $h_n(x_n)$ 不是凸函数、 $f_n(x_n)$ 不是凹函数，但优化问题 $P_4$ 满足 Time-Sharing Condition 时，其对偶间隙仍为0。

令向量 $P_x,P_y$ 和 $P_z$ 是满足 $P_z=\nu P_x+(1-\nu )P_y$ 的功率约束向量（注意：这里的向量 $\nu$ 是只要找到或存在一个属于 $[0,1]$ 区间的 $\nu$ ，使得上述等式成立即可），令 $x_n^{\ast },y_n^{\ast }$ 和 $z_n^{\ast }$ 是在 $P_x,P_y$ 和 $P_z$ 功率约束下优化问题 $P_4$ 的最优解（注意：这里的逻辑是先给出一组满足上述等式的功率约束组 { P x , P y , P z } \{P_x, P_y, P_z\} {Px​,Py​,Pz​} ，然后依据这三个数，分别求出他们对应的最优解 { x n ∗ , y n ∗ , z n ∗ } \{x_n^*,y_n^*,z_n^*\} {xn∗​,yn∗​,zn∗​} ）。

第一步证明：基于 Time-Sharing Condition ，证明 是关于 的凹函数

这里我先给出适当说明，然后再讲述原文步骤，不然直接看原文容易懵逼：
Step（a）先将 ${\sum }_n{f}_n(x_n^{\ast })$ 写为 ${\sum }_n{f}_n(x_n^{\ast }(P_x))$ 的形式；
Step（b）为简洁表示，记 $g(P_x)={\sum }_n{f}_n(x_n^{\ast }(P_x))$ ;
Step（c）因此，我们需要证明：对任意的 $P_x,P_y$ ，对任意的 $\nu \in \left[0,1\right]$，都有 $g(\nu P_x+(1-\nu )P_y)\ge \nu g(P_x)+(1-\nu )g(P_y)$ 成立；
Step（d）也就是需要证明下式成立
$$\begin{array}{rl}\sum _n{f}_n(x_n^{\ast }(\nu P_x+(1-\nu & )P_y))\\ \ge \nu & \sum _n{f}_n(x_n^{\ast }(P_x))+(1-\nu )\sum _n{f}_n(y_n^{\ast }(P_y))\end{array}$$
注意：左式 $x_n^{\ast }(\nu P_x+(1-\nu )P_y)$ 中的 $x_n^{\ast }$ 写法不严谨，需要依据内部的自变量而定。在这里，严谨的应该写为 $q(x_n^{\ast }{y}_n^{\ast })(\nu P_x+(1-\nu )P_y)$ ， 表示是 $P_x$ 与 $P_y$ 的函数多对应的 $x_n^{\ast }$ 与 $y_n^{\ast }$ 的函数。
Step（e）因为 $P_z=\nu P_x+(1-\nu )P_y$ ，所以需要证明下式成立即可：
$$\begin{array}{rl}\sum _n{f}_n(z_n^{\ast }(P_z))\ge \nu & \sum _n{f}_n(x_n^{\ast }(P_x))+(1-\nu )\sum _n{f}_n(y_n^{\ast }(P_y))\end{array}$$
注意：左式直接替换上述等式后，应为 $f_n(x_n^{\ast }(P_z))$，但此时自变量是 $P_z$ 了，因此对应改为 $f_n(z_n^{\ast }(P_z))$ 。

看完前面的解释，再看原文证明步骤，简述如下：
Step（1）因为 Time-Sharing Condition 成立，所以对前文给定的 $P_x,P_y$ 以及给定的 $\nu$，一定存在一个 $\tilde{z}$，使得下式成立：
$$\begin{array}{r}\{\begin{array}{l}\sum _{n=1}^N{h}_n({\tilde{z}}_n)\le \nu P_x+(1-\nu )P_y\\ \sum _{n=1}^N{f}_n({\tilde{z}}_n)\ge \nu \sum _{n=1}^N{f}_n(x_n^{\ast })+(1-\nu )\sum _{n=1}^N{f}_n(y_n^{\ast })\end{array}\end{array}$$
注意：这里的 $\tilde{z}$ 与前文的 $z$ 不一样，但原文中并没有声明，我在推送里区分一下，故用 $\tilde{z}$ 表示。
Step（2）又因为 $\tilde{z}$ 是优化问题可行集内的一个可行点，这意味着该点对应的目标函数一定小于最优解，因此有下式成立：
$$\begin{array}{r}\sum _{n=1}^N{f}_n(z_n^{\ast })\ge \sum _{n=1}^N{f}_n({\tilde{z}}_n)\ge \nu \sum _{n=1}^N{f}_n(x_n^{\ast })+(1-\nu )\sum _{n=1}^N{f}_n(y_n^{\ast })\end{array}$$
Step（3）根据Step(a)-Step(e)的解释可知，上式便是Step(e)中的结论，所以， ${\sum }_n{f}_n(x_n^{\ast })$ 是关于 $P$ 的凹函数得证。

注意：原文没有Step(a)-Step(e)的解释，我看到论文中Step(2)后，最开始不太明白，为什么Step(2)成立后， ${\sum }_n{f}_n(x_n^{\ast })$ 就是关于 $P$ 的凹函数了？后来才想明白的，所以记录在Step(a)-Step(e)的解释里。

第二步证明：利用 ${\sum }_n{f}_n(x_n^{\ast })$ 是关于 $P$ 的凹函数的性质，证明对偶间隙为0

Step（1）考虑到 ${\sum }_n{f}_n(x_n^{\ast })$ 是关于 $P$ 的凹函数，所以我们以 $P$ 为横坐标（等价于以 ${\sum }_n{h}_n(x_n^{\ast })$为横坐标，因为 ${\sum }_n{h}_n(x_n^{\ast })=P$ 显然成立），以 ${\sum }_n{f}_n(x_n^{\ast })$ 为纵坐标，用实线画出如下图所示凹函数：

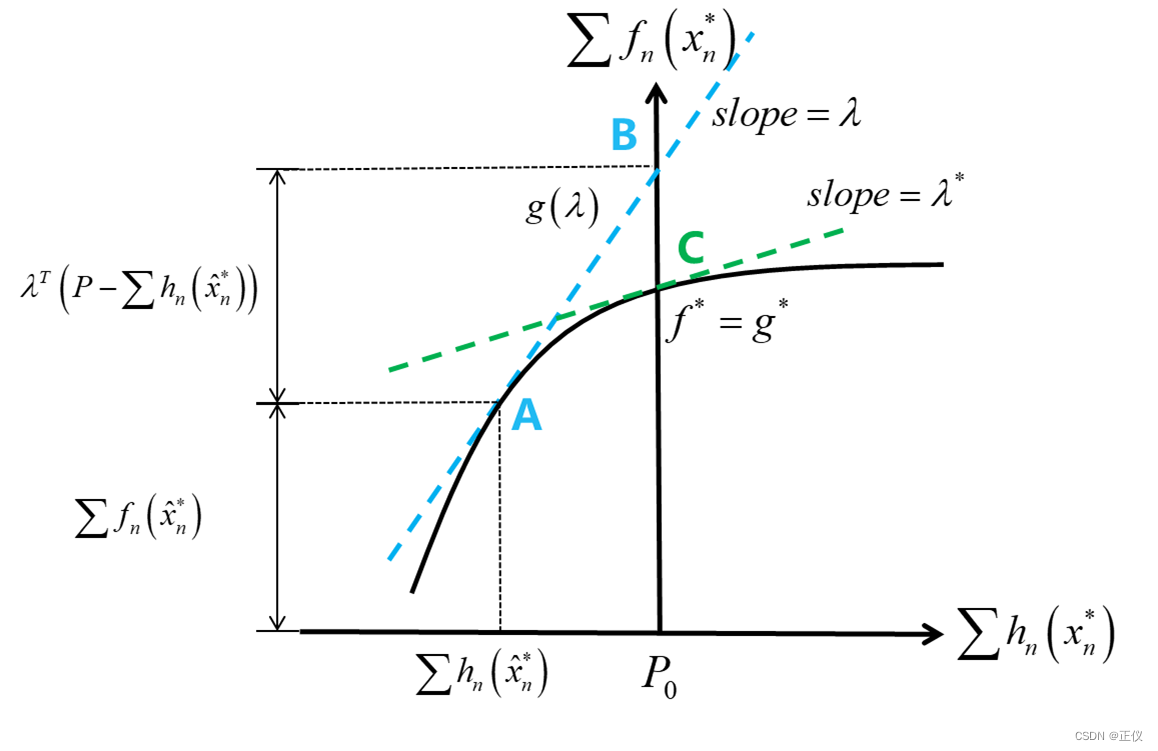
理解：
显然，在变化 $P$ 的时候（即变化 ${\sum }_n{h}_n(x_n^{\ast })$ 的时候）， $x_n^{\ast }$ 也随之而变，导致目标函数 ${\sum }_n{f}_n(x_n^{\ast })$ 也随之而变，所以，可以画出 ${\sum }_n{h}_n(x_n^{\ast })$与 ${\sum }_n{f}_n(x_n^{\ast })$ 之间的变化规律图（即函数图）。而前文证明了，这个函数是凹函数，因此可以做出曲线 $({\sum }_n{h}_n(x_n^{\ast }),{\sum }_n{f}_n(x_n^{\ast }))$ 如图实线所示。

Step（2）又考虑到 $g(\lambda )$ 可写成下式：
$$\begin{array}{rl}g(\lambda )& ={\max }_{x_n}\left(\sum _n{f}_n(x_n)+{\lambda }^T\left(P-\sum _n{h}_n(x_n)\right)\right)\end{array}$$

令 ${\hat{x}}_n^{\ast }$ 是上述优化问题的最优解，则 $g(\lambda )$ 可写为下式：

$$g(\lambda )=\sum _n{f}_n({\hat{x}}_n^{\ast })+{\lambda }^T\left(P-\sum _n{h}_n({\hat{x}}_n^{\ast })\right)$$

显然， $g(\lambda )$ 是关于 $P$ 的线性函数，且斜率为 $\lambda$ 。因此，根据其几何意义，我们可在曲线 $({\sum }_n{h}_n(x_n^{\ast }),{\sum }_n{f}_n(x_n^{\ast }))$ 上，做一条切线，且切点为 $({\sum }_n{h}_n({\hat{x}}_n^{\ast }),{\sum }_n{f}_n({\hat{x}}_n^{\ast }))$ 。此外，这条切线与纵坐标的交点为 ${\sum }_n{f}_n({\hat{x}}_n^{\ast })+{\lambda }^T\left(P-{\sum }_n{h}_n({\hat{x}}_n^{\ast })\right)$ ，而这个交点，便是 $g(\lambda )$ 的确切取值（即图中的点 $B$ ）。

Step（3）对偶问题中，需要通过寻找 $\lambda$，以最小化 $g(\lambda )$ ，记最优解为 $g^{\ast }$ 。显然，只有当曲线 $({\sum }_n{h}_n(x_n^{\ast }),{\sum }_n{f}_n(x_n^{\ast }))$ 是凹的，此时在整条曲线上寻找最优的切线斜率 $\lambda$ 时，才可以找到最优的 ${\lambda }^{\ast }$ 。此时， $g(\lambda )$ 与纵坐标交点的最小值就等于曲线自身的最小值，即：f^*=g* ，如图中点 $C$ 所示。

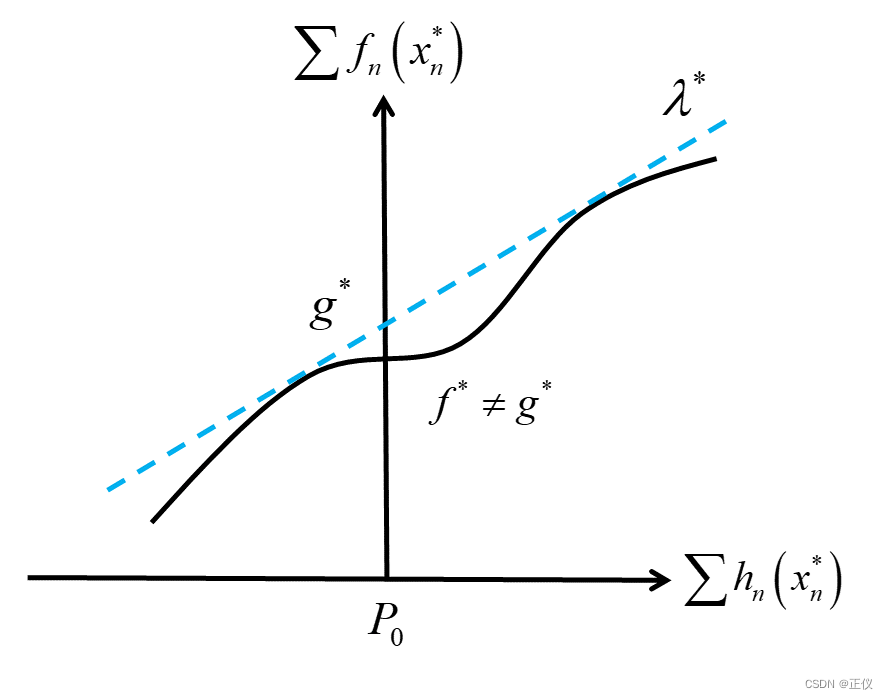
Step（4）为了说明 Time-Sharing Condition 的重要性，下图说明了当该条件不成立的时候，对偶间隙不为0。

PART III ：用Time-Sharing Condition解释问题2

方案1： 如果OFDM系统可以实现完美的时分复用功能，则 Time-Sharing Condition 显然满足，直观解释如下：
令 $x_n$ 与 $y_n$ 是两种功率分配方案。在这种情况下，全部的频谱带宽可以以 $\nu$ 的比率分配给策略 $x_n$ ，以 $1-\nu$ 的比例分给策略 $y_n$ 。此时，原始的目标函数变为两套方案的线性组合，即：
$$\sum _n{f}_n=\sum _n\left[\nu f_n(x_n)+(1-\nu )f_n(y_n)\right]$$
与此同时，约束也是时隙分配的线性组合，此时为线性关系，自然满足 Time-Sharing Condition中的凹性与凸性 。

方案2： 如果OFDM系统可以实现频分复用功能，且子载波数 $N\to +\inf$ ，此时，通过在频域上按比例 $\nu$ 交错 $x_n$ 与 $y_n$ ，则也可以得到上述结论。

参考文献：

[1]祁忠勇.信号处理与通信中的凸优化: 从基础到应用,2019:300-302.
[2]Yu W, Ginis G, Cioffi J M. Distributed multiuser power control for digital subscriber lines[J]. IEEE Journal on Selected areas in Communications, 2002, 20(5): 1105-1115.
[3]Cendrillon R, Yu W, Moonen M, et al. Optimal multiuser spectrum balancing for digital subscriber lines[J]. IEEE Transactions on Communications, 2006, 54(5): 922-933.
[4]Yu W, Lui R. Dual methods for nonconvex spectrum optimization of multicarrier systems[J]. IEEE Transactions on communications, 2006, 54(7): 1310-1322.

文字 | 正仪
编辑 | 正仪
作图 | 正仪

更多优化内容，欢迎关注本人微信公众号：优化与博弈的数学原理

最后，助大家学业有成！早日毕业~