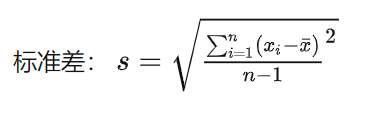M.Wring Books
问从1到n所有数的数位加起来一共是多少
假设n为1025
我们分别从个位,十位,百位,...考虑
对于个位,1到1025每个数都有个位,所以加1025
对于十位,1到1025中1到9没有十位,所以加1025-9
对于百位,1到1025中1到99没有百位,所以加1025-99
对于千位,1到1025中1到999没有千位,所以加1025-999
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
using namespace std;
typedef long long ll;
void solve(){
int x;
cin>>x;
string s=to_string(x);
int len=s.size()-1;
ll res=x;
int t=9;
for(int i=1;i<=len;i++){
res+=x-t;
t=t*10+9;
}
cout<<res<<endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}C.Beautiful Sequence
找到b[i]的最高位的1,由于b[i]=a[i]^a[i+1],又因为数组a非降序,所以a[i]的该位肯定是0(a[i]和a[i+1]的该位一位是0一位是1,又因为数组非降序)
然后根据将b[1],b[2],...b[i-1]全部异或起来,比如说
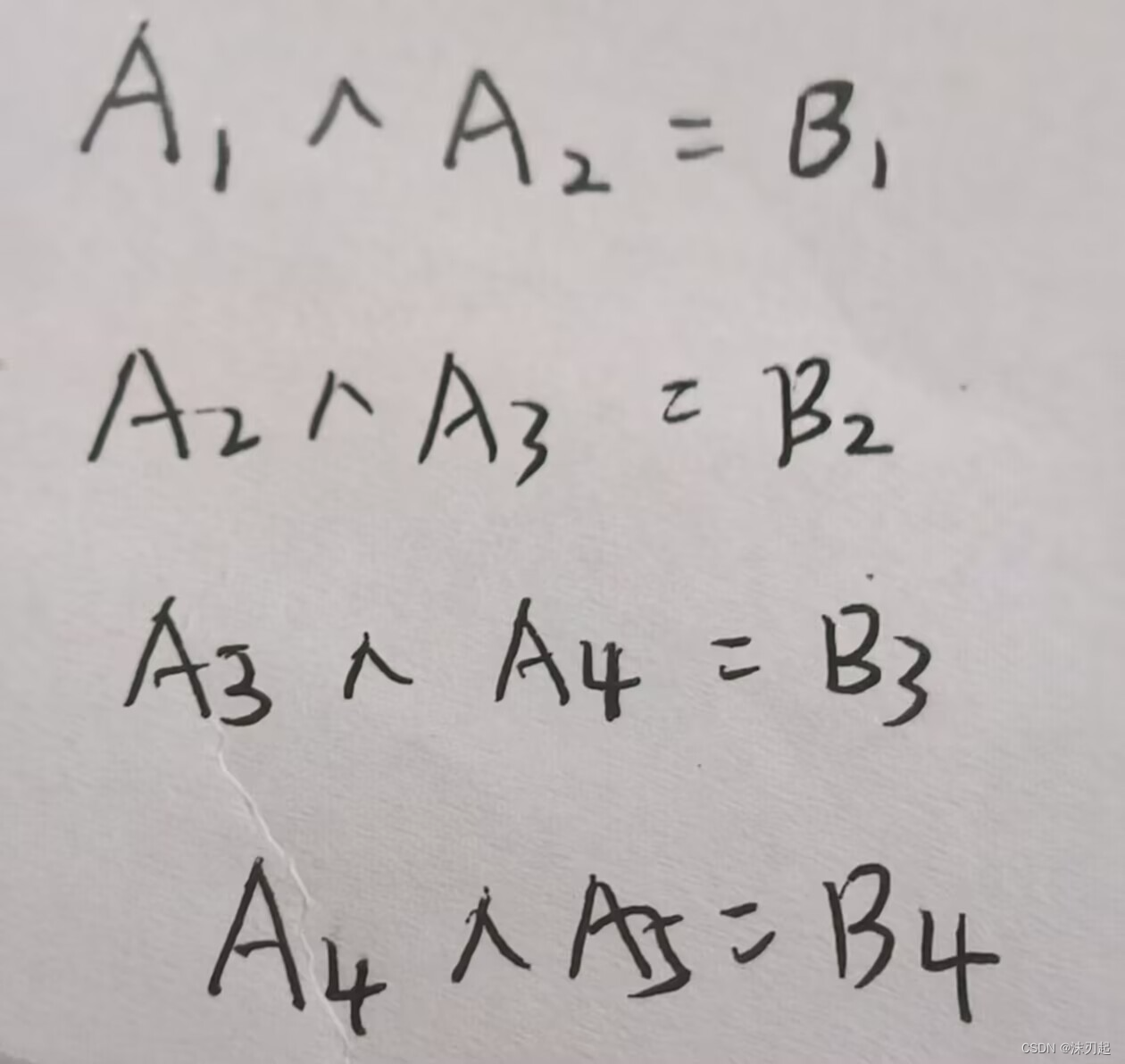
b[1],b[2],b[3],b[4],b[5]全部异或起来,然后中间a[2],a[3],a[3],a[4]都被抵消了,只剩下a[1]和a[5]的异或了,然后a[5]的某一位已经确定为0了,所以就能确定a[1]的这一位了
如果a[1]确定了,我们就能通过递推关系确定整个a序列,所以我们的任务就是确定a[1]
对于a[1]没有确定的位,我们就自己填充,具体解释见注释
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#include<cmath>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=1e6+10;
int a[N],b[N];
int space[31];
int n,k;
//求x的最高位的1是第几位
inline int highbit(int x) {
//从2^30开始,即第31位开始,不断左移,如果遇到哪一位为1,就返回是第几位
for(int t=1<<30,cnt=31; t>0; t>>=1,cnt--) {
if(x&t) return cnt;
}
return -1;
}
void solve() {
memset(space,0,sizeof space);
cin>>n>>k;
for(int i=1; i<n; i++) cin>>b[i];
for(int i=1; i<n; i++) {
if(highbit(b[i])!=-1&&space[highbit(b[i])]==0) space[highbit(b[i])]=i;//假设space[cnt]为x,a[i]的第x位必定是0
}
k--;//k为1的时候第一小的二进制数是0000,k为2的时候第二小的二进制数是0001,以此类推
//所以k--得到的二进制数就是我们要填充的未确定的位
int pos=1;
a[1]=0;//初始a[1]设为0,表示一位都没有填充,没有填充每一位都为0
//i从1开始乘2,小于等于2^29,a数组和b数组最高达不到2^29,29位就足够了
//那么为什么不能到30位呢,因为a数组和b数组都达不到30位,当k为2^30时,pos到达2^30,导致a[1]+=2^30并成功输出a数组,但是a并没有第30位,导致错误
//cnt即表示第几位(最低位为1,右边为低位),从最低位枚举到第29位
for(int i=1,cnt=1; i<=(1<<29); i<<=1,cnt++) {
//如果第cnt位的space值不等于0,假设x为space[cnt],那么a[x]的第cnt位必定为0
if(space[cnt]) {
int tmp=0;
//假设sapce[cnt]为x,那么j从x-1枚举到1
//tmp初始为0,然后和b[1],b[2],...b[x-1]异或,即把b[1],b[2],...b[x-1]全部异或
//tmp即为a[1]^a[x],a[x]的第cnt位必定为0,然后a[1]的第cnt位和0进行异或得到的仍是a[1]的第cnt位,然后i是第cnt位为1,其它位均为0的二进制数,然后
//和i进行与运算,就仅仅保留a[1]的第cnt位,于是我们就确定了a[1]的第cnt位是多少
for(int j=space[cnt]-1; j>0; j--) tmp^=b[j];
tmp&=i;
a[1]+=tmp;
}
//如果第cnt位的space值不等于0,说明第cnt位不能确定,那么就自己填充,确定的位我们已经改变不了了,然后未确定的位我们可以选择填充0还是1
//那么具体如何填充呢?因为我们要使得字典序是第k小的,所以我们未确定的位就和k(已经减过1了)的二进制对照,从最低位开始,第i次使用k(已经减过1了)的第i低的位进行填充
//pos表示二进制,pos不断左移,从1到10到100到1000...
else {
if(pos>k) continue;//如果已经填充为第k小的了,那么就不用继续填充了,前面补前导0就行了,而每一位本身就是0,所以根本无需操作,直接continue
if(k&pos) a[1]+=i;//如果k的这一位为1,那么就将a[1]的这一位改为1
pos<<=1;//pos左移一位
}
}
//pos由于最后多移动了一位,所以我们填充的其实少一位,这也就是为什么要取等号的原因,所以当pos小于等于k时,说明没有填充到第k小,输出-1
if(pos<=k) {
cout<<-1<<endl;
return;
}
//我们已经确定出了a[1],现在我们只要根据a[1]来确定出整个a数组,然后验证其合法性即可
for(int i=2; i<=n; i++) {
a[i]=a[i-1]^b[i-1];//a[i]^a[i+1]=b[i],两边同时异或一个a[i],得a[i+1]=a[i]^b[i]
if(a[i]<a[i-1]) {
cout<<-1<<endl;
return;
}
}
for(int i=1; i<=n; i++) cout<<a[i]<<" ";
cout<<endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}I.We love Strings
k>>1相当于k/2
k>>=1相当于k/=2
按字符串长度进行分类
当字符串长度小于等于20时,直接暴力枚举所有可能的字符串,放入set中,由于set会自动去重,所以只要返回set中的元素个数就行了
当字符串长度大于20时,对于长度为i的所有字符串,枚举所有选与不选这些字符串的二进制串,根据容斥原理算满足的个数(具体解释见注释)
证明见2023牛客暑假多校 C I M 题解 | JorbanS_JorbanS的博客-CSDN博客
容斥原理:


AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<set>
#include<queue>
#include<cmath>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=410,mod=998244353;
vector<string>s[N];
set<string>st;
string tmp;
int n;
void dfs(string s,int len,int cur) {
//s为当前已经生成的字符串
//cur表示当前填了几个了
if(s.size()==len) {
st.insert(s);
return;
}
//tmp是题目所给的字符串,s是我们自己构造的字符串,当前字符为?时,改成0或1,当前字符本来就为0或1时,那么直接就是原来的字符
if(tmp[cur]=='?') {
dfs(s+'1',len,cur+1);//始终搜长度为len的字符串
dfs(s+'0',len,cur+1);
} else {
dfs(s+tmp[cur],len,cur+1);
}
}
void solve() {
cin>>n;
for(int i=1; i<=n; i++) {
string ss;
cin>>ss;
int sz=ss.size();//字符串的长度
s[sz].push_back(ss);//长度相同的字符串都放在一个容器里
}
int ans=0;
//枚举字符串的长度
for(int i=1; i<=400; i++) {
if(!s[i].size()) continue;//如果没有长度为i的字符串,那么就continue
//如果字符串长度小于等于20
if(i<=20) {
for(auto ss:s[i]) {
tmp=ss;
dfs("",i,0);//从空字符串开始搜,搜所有长度为i的字符串
}
}
//如果字符串长度大于20
else {
int num=s[i].size();//长度为i的字符串有几个
int m=1<<num;//m为2^num
//枚举j从1到2^num-1,2^num-1为非空子集的个数(子集的个数为2^num,然后去掉空集,也就是说我们至少选择一个字符串)
//可以用0表示不选该字符串,用1表示选该字符串,然后所有num个字符串的选与不选用二进制串表示,然后去掉全是0的二进制串
//枚举所有长度为i的字符串的所有组合状态,每个字符串的选与不选
for(int j=1; j<m; j++) {
int cnt=0;//记录当前处理的字符串个数
bool ok=true;//标记该二进制串是否符合条件
string tmps;
for(int k=0; k<i; k++) tmps+='?'; //临时字符串tmps(长度为i)初始化为i个'?',看tmps能否变成一个串满足我们所选的所有字符串,计入个数cnt,如果cnt为奇数,说明奇数个字符串可以表示成一样的,也就是说
//奇数个集合相交的排列组合的方式是一样的,根据容斥原理,加上奇数个相交的部分,减去偶数个相交的部分
//遍历长度为i的字符串数组s[i]中的每一个字符串s[i][t]
for(int t=0; t<num; t++) {
//判断当前字符串是否被选,j是一个二进制串,然后取每一位看是否为1,即看该字符串是否被选,该位为1则表示该字符串被选
if(j>>t&1) {
cnt++;
//遍历长度为i的字符串s[i][t]中的每一个字符s[i][t][tt]
for(int tt=0; tt<i; tt++) {
//判断当前位置是否为问号,如果为问号,则更新为s[i][t][tt]的值
if(tmps[tt]=='?') {
if(s[i][t][tt]!='?') tmps[tt]=s[i][t][tt];
//如果当前位置不是问号并且不相等,则标记为不满足条件
} else if(s[i][t][tt]!=tmps[tt]) {
ok=false;
break;
}
}
}
}
if(!ok) continue;
int mi=1;
for(int k=0;k<i;k++){
if(tmps[k]=='?') mi=mi*2%mod;//最后如果能将选中的字符串表示成一样的,那么该种字符串的排列组合即为2^x(x为问号的个数)
}
//容斥原理
if(cnt&1) ans=(ans+mi)%mod;
else ans=(ans-mi+mod)%mod;
}
}
}
ans=(ans+st.size())%mod;
cout<<ans<<endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
// cin>>t;
while(t--)
solve();
return 0;
}