2023 CCF BDCI 基于飞桨实现花样滑冰选手骨骼点动作识别 16名方案以及总结
比赛任务
花样滑冰与其他运动项目相比,其动作类型的区分难度更大,这对识别任务来说是极大的挑战。对于花样滑冰动作识别任务,主要难点如下:
(1) 花样滑冰运动很难通过一帧或几帧图像中的人物姿态去判断动作类别;
(2) 花样滑冰相同大类、不同小类的两个动作类别仅存于某几帧的细微差异,判别难度极高。然而,其他帧的特征也必须保留,以便用于大类识别以及“多义帧”处理等情况。
基于现实场景的应用需求以及图深度学习模型的发展,本次比赛旨在通过征集各队伍建立的高精度、细粒度、意义明确的动作识别模型,探索基于骨骼点的时空细粒度人体动作识别新方法。本次比赛将基于评价指标Accuracy对各队伍提交结果的评测成绩进行排名,Accuracy得分越高,则认为该模型的动作识别效果越好。
1.类别定义:
花样滑冰动作包括3个大类,分别为跳跃、旋转和步法,每个大类又包含很多小类。例如,跳跃大类包含:飞利浦三周跳(3Filp)和勾手三周跳(3Lutz)2个小类。然而,这2类跳跃的判别性仅在于一些个别帧的差异。此外,如果想就跳跃小类(3Filp或3Lutz)与旋转小类进行区别,对大部分帧的特征加以使用才能产生较好的判别性。
2.多义帧:
花样滑冰动作不同类别中相似的帧,甚至存在个别帧的特征相同等情况。
3.具体任务:
参赛选手利用比赛提供的训练集数据,构建基于骨骼点的细粒度动作识别模型,完成测试集的动作识别任务。模型识别效果由指标Accuracy排名决定,Accuracy得分越高,则认为该模型的动作识别效果越好。
数据集介绍
本次比赛数据集旨在借助花样滑冰选手的视频图像研究人体运动。由于花样滑冰选手动作切换速度十分迅速,如希望准确判断一个动作的类别,只靠随机抽取的几帧很难出色地完成任务。
尽管目前人体运动分析研究领域主流的视频数据集较多,规模也较大,如视频识别数据集:Kinetics、 Moments in Time、UCF101等,视频分割数据集:Breakfast、Epic Kitchens、Salads50等。然而,以上数据集大多缺乏人体运动的特性(Kinetics有部分运动特性,但不够专业,且类别有限)。举例来看,若对UCF101数据集选取子集,遮挡住数据中人物并留下场景,目标检测结果的准确率仅下降较小幅度,这说明该视频数据不太关注人的运动,也无法体现视频分析的特性。相比之下,本次比赛数据集旨在借助花样滑冰选手的视频图像研究人体运动。在花样滑冰运动中,人体姿态和运动轨迹相较于其他运动呈现出复杂性强、类别众多等特点,有助于开展对细粒度图深度学习新模型、新任务的研究。
在本次比赛最新发布的数据集中,所有视频素材均从2017-2020 年的花样滑冰锦标赛中采集得到。源视频素材中视频的帧率被统一标准化至每秒30 帧,图像大小被统一标准化至1080 * 720 ,以保证数据集的相对一致性。之后通过2D姿态估计算法Open Pose,对视频进行逐帧骨骼点提取,最后以.npy格式保存数据集。请各位选手基于本次比赛最新发布的训练集数据训练模型,并基于本次比赛最新发布的测试集数据提交对应结果文件。
数据集构成
|–train.zip
|–train_data.npy
|–train_label.npy
|–test_A.zip
|–test_A_data.npy
|–test_B.zip
|–test_B_data.npy
本次比赛最新发布的数据集共包含30个类别,训练集共2922个样本,A榜测试集共628个样本,B榜测试集共634个样本;
train_label.npy文件通过np.load()读取后,会得到一个一维张量,张量中每一个元素为一个值在0-29之间的整形变量,代表动作的标签;
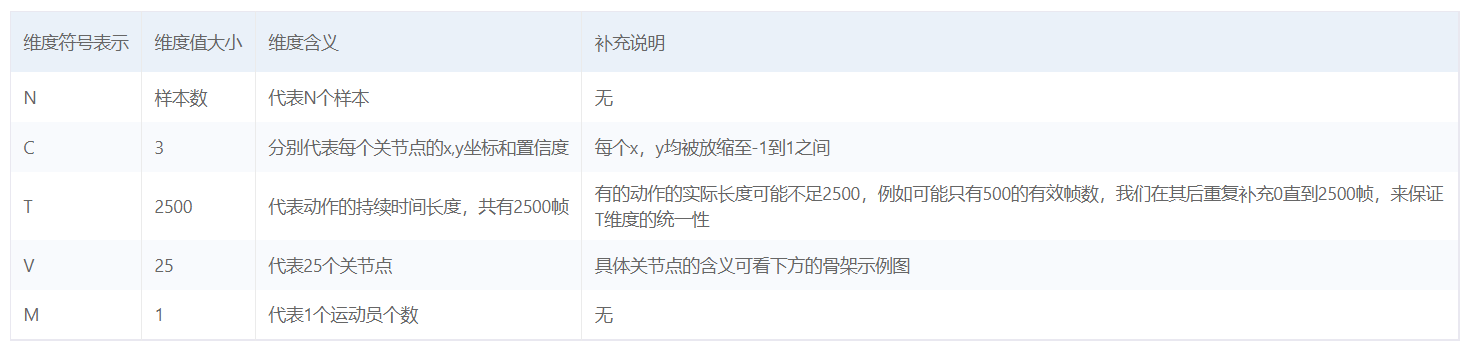
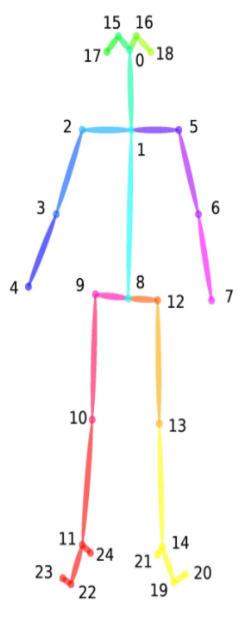
data.npy文件通过np.load()读取后,会得到一个形状为N×C×T×V×M的五维张量,每个维度的具体含义如下:
训练集: 下载
A榜测试集:下载
B榜测试集:下载
数据预处理
首先拆分数据集,使用jikuai库里面的npysplit,拆分后存盘到用户根目录。
from jikuai.dataset import npysplit
import numpy as np
npysplit("data/data104925/train_data.npy", "data/data104925/train_label.npy", 0.8)
模型选择
ST-GCN、AGCN(AAGCN)、MS-G3D、PoseC3D
GCN
GCN步骤(假设图输入为X),可以视为
- 对图输入X(X表示图每个节点的特征)进行特征提取(假设参数为W),输出XW。微观来看,这个特征提取可以理解为对图上每个节点的特征进行了分别提取,其特征维度从[公式]变化到[公式];
- 根据图结构中建立一个邻接矩阵A,并对其进行归一化or对称归一化,获得A;
- 利用归一化的邻接矩阵A对提取后的特征XW进行聚合,聚合的结果为AXW。
这样一来,基本的图卷积运算就实现了。其具体的实现代码如下所示:
class GraphConvolution(nn.Module):
def __init__(self, input_dim, output_dim, use_bias=True):
"""图卷积:L*X*\theta
Args:
----------
input_dim: int
节点输入特征的维度
output_dim: int
输出特征维度
use_bias : bool, optional
是否使用偏置
"""
super(GraphConvolution, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.use_bias = use_bias
self.weight = nn.Parameter(torch.Tensor(input_dim, output_dim))
if self.use_bias:
self.bias = nn.Parameter(torch.Tensor(output_dim))
else:
self.register_parameter('bias', None)
self.reset_parameters()
def reset_parameters(self):
init.kaiming_uniform_(self.weight)
if self.use_bias:
init.zeros_(self.bias)
def forward(self, adjacency, input_feature):
"""邻接矩阵是稀疏矩阵,因此在计算时使用稀疏矩阵乘法
Args:
-------
adjacency: torch.sparse.FloatTensor
邻接矩阵
input_feature: torch.Tensor
输入特征
"""
device = "cuda" if torch.cuda.is_available() else "cpu"
support = torch.mm(input_feature, self.weight.to(device))
output = torch.sparse.mm(adjacency, support)
if self.use_bias:
output += self.bias.to(device)
return output