图像梯度

• 图像梯度，图像边界等
• 使用到的函数有： cv2.Sobel()， cv2.Scharr()， cv2.Laplacian() 等
• 原理：梯度简单来说就是求导。OpenCV 提供了三种不同的梯度滤波器，或者说高通滤波器： Sobel，Scharr 和 Laplacian。Sobel， Scharr 其实就是求一阶或二阶导数。 Scharr 是对 Sobel（使用小的卷积核求解求解梯度角度时）的优化。 Laplacian 是求二阶导数。

Sobel 算子和 Scharr 算子

Sobel 算子是高斯平滑与微分操作的结合体，所以它的抗噪声能力很好。你可以设定求导的方向（ xorder 或 yorder）。还可以设定使用的卷积核的大小（ ksize）。如果 ksize=-1，会使用 3x3 的 Scharr 滤波器，它的的效果要比 3x3 的 Sobel 滤波器好（而且速度相同，所以在使用 3x3 滤波器时应该尽量使用 Scharr 滤波器）。 3x3 的 Scharr 滤波器卷积核如下：
$$X方向=\left[\begin{array}{ccc}-3& 0& 3\\ -10& 0& 10\\ -3& 0& 3\end{array}\right],Y方向=\left[\begin{array}{ccc}-3& -10& -3\\ 0& 0& 0\\ 3& 10& 3\end{array}\right]$$

Laplacian 算子

拉普拉斯算子可以使用二阶导数的形式定义，可假设其离散实现类似于二阶 Sobel 导数，事实上， OpenCV 在计算拉普拉斯算子时直接调用 Sobel 算子。
拉普拉斯滤波器使用的卷积核：
$$kernel=\left[\begin{array}{ccc}0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}\right]$$

import numpy as np
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('./resource/opencv/image/sudoku.png', cv2.IMREAD_GRAYSCALE)

# 拉普拉斯 cv2.CV_64F 输出图像的深度（数据类型），可以使用-1, 与原图像保持一致 np.uint8
laplacian = cv2.Laplacian(img, cv2.CV_64F, ksize=3)
laplacian = cv2.convertScaleAbs(laplacian)  

# 索贝尔 X方向, 参数 1,0 为只在 x 方向求一阶导数，最大可以求 2 阶导数
sobelx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=5)
sobelx = cv2.convertScaleAbs(sobelx)

# 索贝尔 Y方向, 参数 0,1 为只在 y 方向求一阶导数，最大可以求 2 阶导数
sobely = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=5) 
sobely = cv2.convertScaleAbs(sobely)

# Scharr X方向,
scharrx = cv2.Scharr(img, cv2.CV_64F, 1, 0)
scharrx = cv2.convertScaleAbs(scharrx)

# Scharr Y方向,
scharry = cv2.Scharr(img, cv2.CV_64F, 0, 1)
scharry = cv2.convertScaleAbs(scharry)

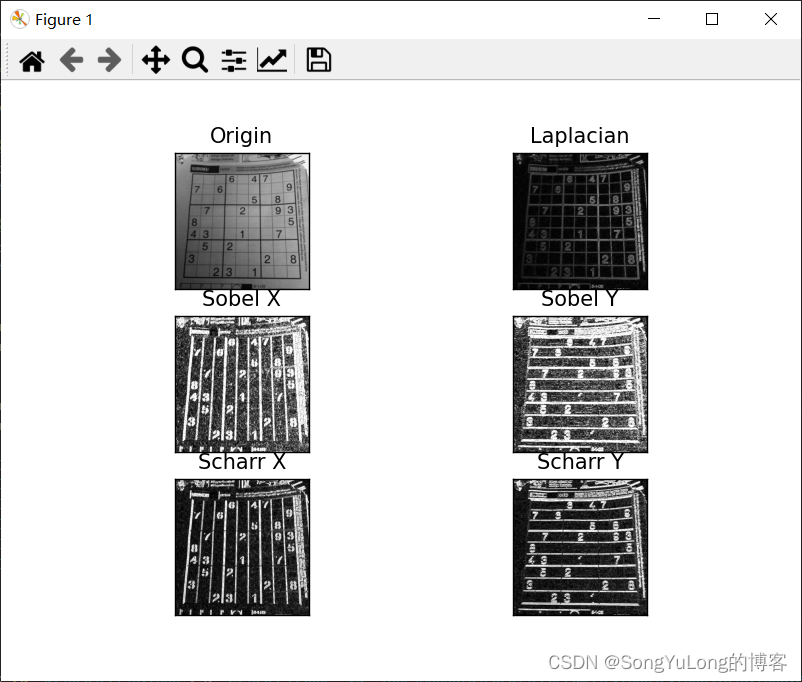
plt.subplot(321), plt.imshow(img, cmap='gray'), plt.title('Origin'), plt.xticks([]), plt.yticks([])
plt.subplot(322), plt.imshow(laplacian, cmap='gray'), plt.title('Laplacian'), plt.xticks([]), plt.yticks([])
plt.subplot(323), plt.imshow(sobelx, cmap='gray'), plt.title('Sobel X'), plt.xticks([]), plt.yticks([])
plt.subplot(324), plt.imshow(sobely, cmap='gray'), plt.title('Sobel Y'), plt.xticks([]), plt.yticks([])
plt.subplot(325), plt.imshow(scharrx, cmap='gray'), plt.title('Scharr X'), plt.xticks([]), plt.yticks([])
plt.subplot(326), plt.imshow(scharry, cmap='gray'), plt.title('Scharr Y'), plt.xticks([]), plt.yticks([])
plt.show()

import numpy as np
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('./resource/opencv/image/box2.png')


# output dtype = cv2.CV_8U
sobelx8u = cv2.Sobel(img, cv2.CV_8U, 1,0, ksize=5)

# 也可以将参数设置为-1
sobelx8u_n = cv2.Sobel(img, -1, 1, 0, ksize=5)

# output dtype = cv2.CV64F,
sobelx64f = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=5)
abs_sobel64f = np.absolute(sobelx64f)
sobel_8u = np.uint8(abs_sobel64f)

# Scharr X方向
scharrx = cv2.Scharr(img,cv2.CV_64F,1,0)

# Scharr Y方向
scharry = cv2.Scharr(img,cv2.CV_64F,0,1)


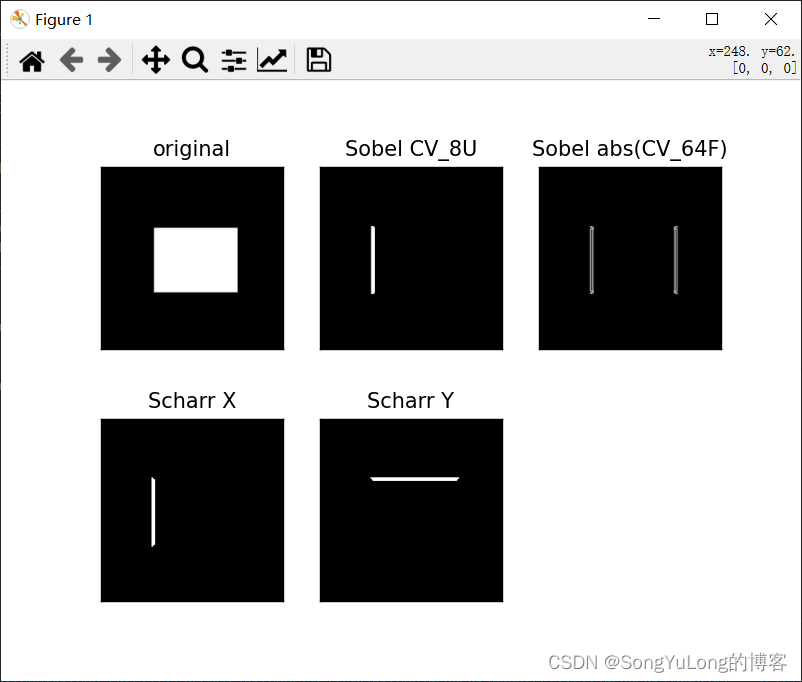
plt.subplot(2,3,1), plt.imshow(img, cmap='gray'), plt.title('original'), plt.xticks([]), plt.yticks([])
plt.subplot(2,3,2), plt.imshow(sobelx8u, cmap='gray'), plt.title('Sobel CV_8U'), plt.xticks([]), plt.yticks([])
plt.subplot(2,3,3), plt.imshow(sobel_8u, cmap='gray'), plt.title('Sobel abs(CV_64F)'), plt.xticks([]), plt.yticks([])
plt.subplot(2,3,4), plt.imshow(scharrx, cmap='gray'), plt.title('Scharr X'), plt.xticks([]), plt.yticks([])
plt.subplot(2,3,5), plt.imshow(scharry, cmap='gray'), plt.title('Scharr Y'), plt.xticks([]), plt.yticks([])
plt.show()