各种查找算法的效率
- 顺序查找
- 一般顺序表(没有顺序,随机排列)
- 成功时平均查找长度: 1 + . . . + n n = n + 1 2 \frac{1+...+n}{n}=\frac{n+1}{2} n1+...+n=2n+1
- 失败时平均查找长度: n n n
- 有序顺序表(按照递增或递减排列)

- 成功时平均查找长度: 1 + . . . + n n = n + 1 2 \frac{1+...+n}{n}=\frac{n+1}{2} n1+...+n=2n+1
- 失败时平均查找长度: 1 + 2 + . . . + n + n n + 1 = n 2 + n n + 1 \frac{1+2+...+n+n}{n+1}=\frac{n}{2}+\frac{n}{n+1} n+11+2+...+n+n=2n+n+1n
- 一般顺序表(没有顺序,随机排列)
- 折半查找(二分查找)
- 用折半查找法找到给定值的比较次数不会超过树的高度(n个元素的树高为 ⌈ l o g 2 ( n + 1 ) ⌉ \lceil log_2(n+1)\rceil ⌈log2(n+1)⌉)
- 成功时的平均查找长度: A S L = 1 n ( 1 × 1 + 2 × 2 + 3 × 4 + . . . + h × 2 h − 1 = n + 1 n l o g 2 ( n + 1 ) − 1 ≈ l o g 2 ( n + 1 ) − 1 ASL=\frac{1}{n}(1\times 1+2\times 2+3\times 4+...+h\times 2^{h-1}=\frac{n+1}{n}log_2(n+1)-1\approx log_2(n+1)-1 ASL=n1(1×1+2×2+3×4+...+h×2h−1=nn+1log2(n+1)−1≈log2(n+1)−1
- 折半查找的时间复杂度为 O ( l o g 2 n ) O(log_2n) O(log2n)
- 分块查找(索引顺序查找)
- 平均查找长度:
A
S
L
=
L
I
+
L
S
ASL=L_I+L_S
ASL=LI+LS(
L
I
L_I
LI为索引查找的平均查找长度,
L
S
L_S
LS为块内查找的平均查找长度)
- 如将长度为n的查找表均匀地分成b块,每块有s个记录,在等概率情况下,若在块内和索引表中均采用顺序查找,则平均查找长度为 A S L = L I + L S = b + 1 2 + s + 1 2 = s 2 + 2 s + n 2 s ASL=L_I+L_S=\frac{b+1}{2}+\frac{s+1}{2}=\frac{s^2+2s+n}{2s} ASL=LI+LS=2b+1+2s+1=2ss2+2s+n。可见若 s = n s=\sqrt{n} s=n,则平均查找长度取最小值 n + 1 \sqrt{n}+1 n+1
- 平均查找长度:
A
S
L
=
L
I
+
L
S
ASL=L_I+L_S
ASL=LI+LS(
L
I
L_I
LI为索引查找的平均查找长度,
L
S
L_S
LS为块内查找的平均查找长度)
- 树型查找
- 二叉排序树(主要取决于树的高度)
- 若二叉排序树的左右子树高度之差不超过1(即平衡二叉树),则平均查找长度为 O ( l o g 2 n ) O(log_2{n}) O(log2n)
- 若二叉排序树是一个只有左(右)孩子的单支树,则平均查找长度为 O ( n ) O(n) O(n)
- 平衡二叉树(查找过程与二叉排序树相同)
- 平均查找长度为
O
(
l
o
g
2
n
)
O(log_2n)
O(log2n)
- 因为含有n个节点的平衡二叉树的最大深度为 O ( l o g 2 n ) O(log_2n) O(log2n)
- 平均查找长度为
O
(
l
o
g
2
n
)
O(log_2n)
O(log2n)
- 红黑树
- 平均查找长度为 O ( l o g 2 n ) O(log_2n) O(log2n)
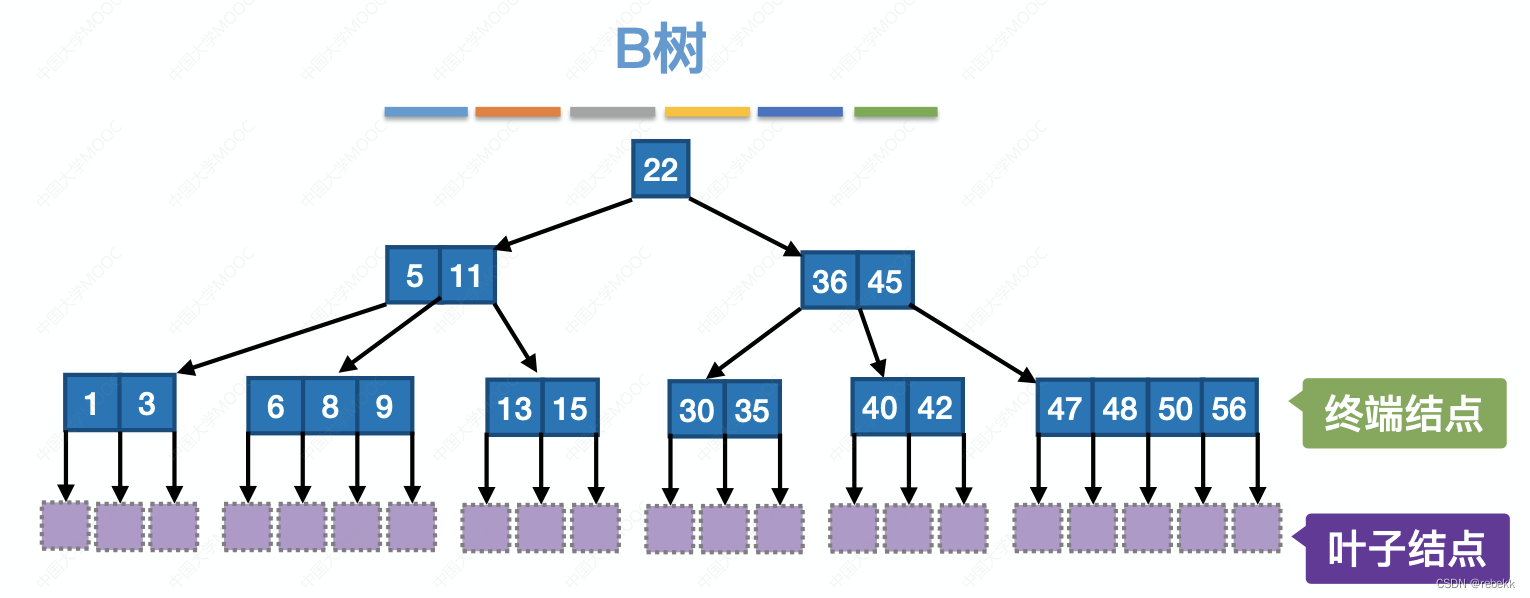
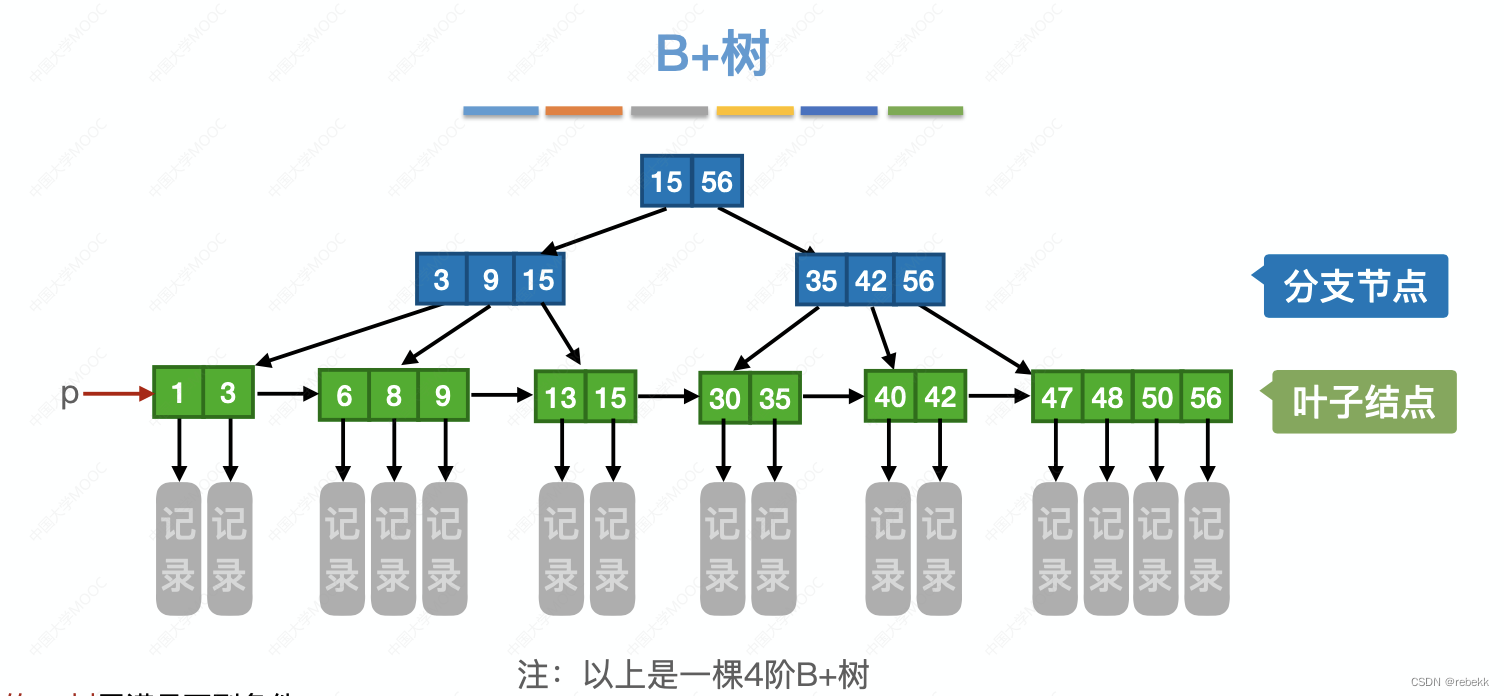
- B树和B+树
- 二叉排序树(主要取决于树的高度)
- 散列表
虽然散列表在关键字与记录的存储位置之间建立了直接映像,但由于冲突的产生,使得散列表的查找过程仍然是一个给定值和关键字进行比较的过程。因此仍需以平均查找长度作为衡量散列表的查找效率的度量。
散列表的查找效率取决于三个因素:散列函数、冲突处理的方法和装填因子。
直观的看, α \alpha α越大,表示装填的记录越满,发生冲突的可能性越大。
折半查找(二分查找)与二叉排序树的区别
二叉排序树与二分查找(折半查找)的查找过程相似,平均时间性能差不多。不同点如下:
- 唯一性:二分查找的判定树唯一,而二叉排序树随着关键字插入顺序不同可能生成不同的二叉排序树
- 插入和删除:二分查找的对象是有序顺序表,若有插入和删除节点的操作,所花的代价是 O ( n ) O(n) O(n);二叉排序树则无需移动节点,只需修改指针即可完成插入和删除操作
- 适用于动态还是静态:当有序表是静态查找表时,宜用顺序表作为其存储结构,采用二分查找实现找操作;若有序表是动态查找表,应选择二叉排序树作为其逻辑结构
平衡二叉树和红黑树的区别
二者的查、插、删的时间复杂度都是 O ( l o g 2 n ) O(log_2n) O(log2n),区别如下:
- 平衡二叉树的插入和删除很容易破坏平衡特性,故插/删后大都需要调整树的形态(计算平衡因子+找到最小不平衡树+LL/RR/LR/RL),这样一来时间开销就很大;而红黑树由于其特性,很多时候插入删除后并不会破坏红黑特性,即便需要调整一般也都可以在常数级时间内完成
- 即虽然二者的插、删、查的时间复杂度都是 O ( l o g 2 n ) O(log_2n) O(log2n),但实际上红黑树的插入和删除性能更好一点,平衡二叉树的查找性能更好一点
- 使用场景:平衡二叉树适用于以查为主、很少插入/删除的场景;红黑树适用于频繁插入、删除的场景,实用性更强
B树和B+树的区别
二者相同点是:除根节点外,最少 ⌈ m 2 ⌉ \lceil\frac{m}{2}\rceil ⌈2m⌉个分叉(确保节点不要太空)。任何一个节点的子树都要一样高(确保绝对平衡)
| - | m阶B树 | m阶B+树 |
|---|---|---|
| 类比 | 二叉查找树的进化 --> m叉查找树 | 分块查找的进化 --> 多级分块查找 |
| 关键字与分叉 | n个关键字对应n+1个分叉(子树) | n个关键字对应n个分叉 |
| 节点包含的信息 | 所有节点中都包含记录的信息 | 只有最下层叶子节点才包含记录的信息(每个节点能存的信息更多,因此可以使树更矮),且叶节点包含所有的关键字 |
| 查找方式 | 不支持顺序查找。查找成功时,可能停在任何一层节点,查找速度不稳定 | 支持顺序查找。查找成功或失败都会到达最下一层节点,查找速度稳定 |