题目

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

示例 1：

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：

2 <= n <= 58

解题思路

1.题目要求我们将绳子剪切为乘积最大的 m 段，这其中蕴含着一个数学问题，就是当我们尽可能将绳子以长度 3等分为多段时，乘积最大。这个推论大家可以自己去证明一下。

2.有了这个推论，这个问题就轻而易举了，

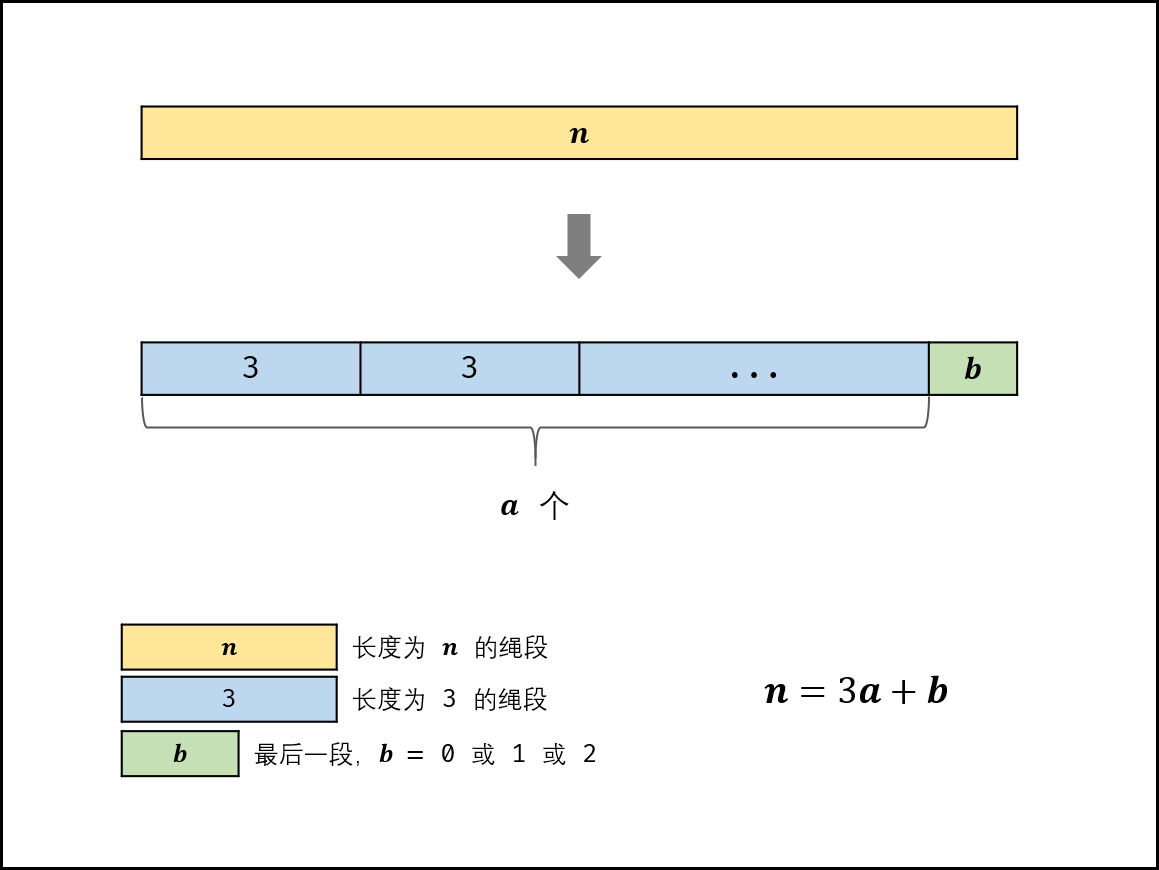
①切分规则：
最优： 3 。把绳子尽可能切为多个长度为 3 的片段，留下的最后一段绳子的长度可能为 0,1,2 三种情况。
次优： 2。若最后一段绳子长度为 2 ；则保留，不再拆为 1+1 。
最差： 1。若最后一段绳子长度为 1 ；则应把一份 3+1 替换为 2+2，因为 2×2>3×1
②算法流程：

当 n≤3 时，按照规则应不切分，但由于题目要求必须剪成 m>1 段，因此必须剪出一段长度为 1 的绳子，即返回 n−1 。
当 n>3 时，求 n 除以 3 的整数部分 res 和余数部分 mod （即 n=3res+ mod =），并分为以下三种情况：

①当 b=0 时，直接返回 3^a；

②当 b=1 时，要将一个 1+3 转换为 2+2，因此返回 3^{a-1} *4

③当 b=2 时，返回 3^a*2

代码实现

class Solution {
    public int cuttingRope(int n) {
        if(n <= 2){
            return 1;
        }
        if(n == 3){
            return 2;
        }
        int res = n / 3;
        int mod = n % 3;
        if(mod == 0){
            return pow(3,res);
        }else if(mod == 1){
            return pow(3,res - 1) * 4;
        }else {
            return pow(3,res) * 2;
        }

    }
    int pow(int i, int k){
        int sum = 1;
        for(i = 1; i <= k; i++){
            sum = sum * 3;
    }
    return sum;
    }
    
}