代码随想录算法训练营第24天| 第七章回溯算法part01 理论基础、leetcode 77

news2024/9/22 17:20:48

Part I : 回溯算法基础

背景：一直以来都是半懂不懂的，在逻辑上不难，毕竟属于暴力搜索；在代码上就开始缠绕起来了，自己研究的时候对N皇后问题老是理不清。这次终于在Carl这开始前进啦！
何为回溯算法：回溯算法(backtracking algorithm)其实就是走到尽头后返回上一步，再从上一步选别的方向出发走到另一个尽头，直到穷尽上一步的所有方向的结果，不断递归。如图所示：
为什么需要用回溯算法：迭代法是最常用的一种暴力搜索法，但有些问题规模一大起来就不适用了，比如组合问题，给100个数搜50个数的组合，怎么办？这时用回溯就可以解决。下面是Carl列出的回溯适用的场景。
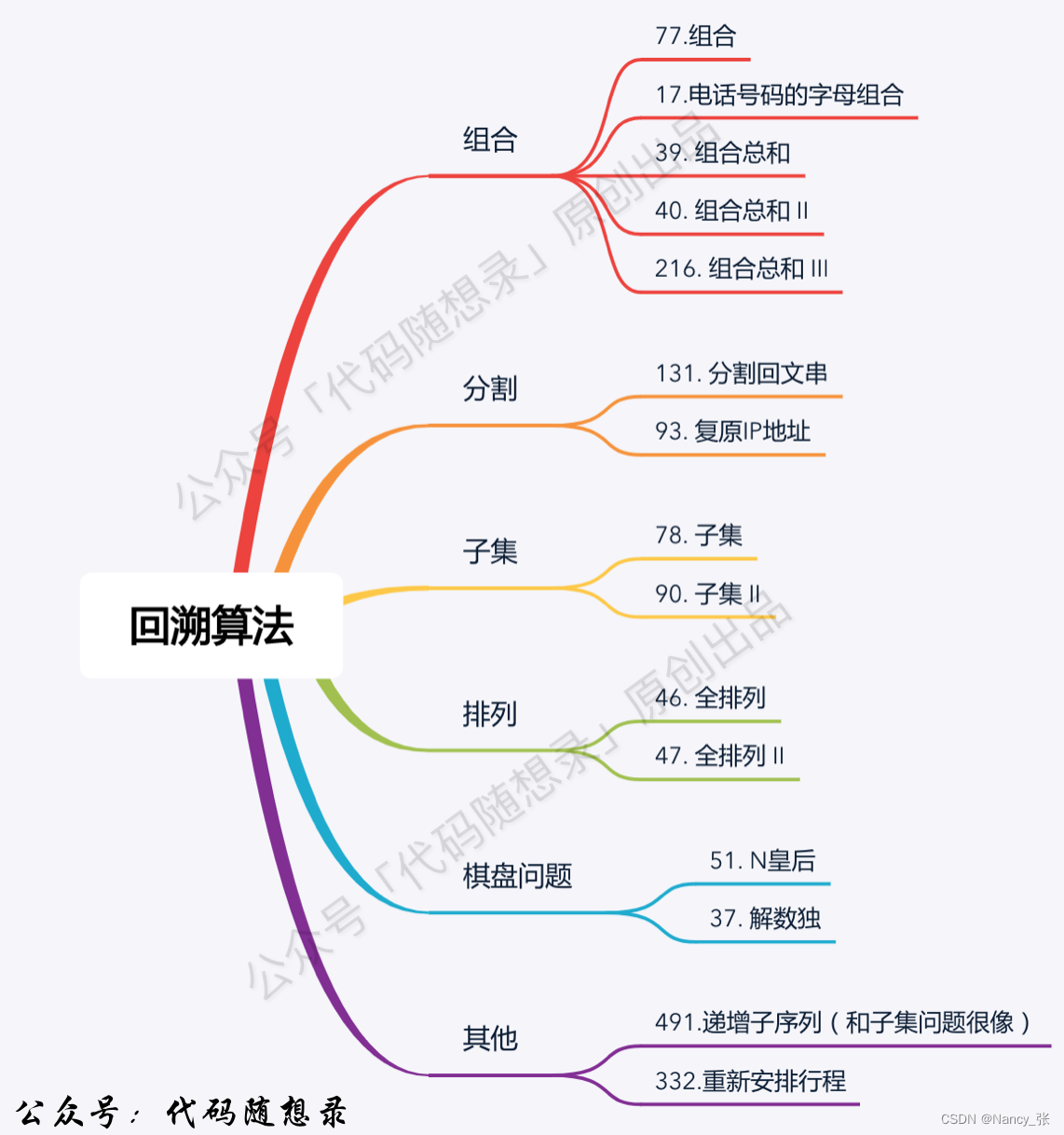
回溯算法与递归的关系：根据Carl所说，回溯是递归的副产品，只要有递归就会有回溯。可以理解为回溯函数也就是递归函数，指的都是一个函数。不过平时我们写的大部分递归在写法上隐藏了回溯过程。
回溯算法的理解与代码模版：

回溯三部曲
第一步：回溯函数模板返回值（通常返回为空）以及参数（不好确定，可以后面补齐）
第二步：回溯函数的终止条件
第三步：回溯搜索的遍历过程

  // 回溯三部曲确定的模板框架
    void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

针对第三步的理解如下（凡是递归或回溯都可以还原到树形结构）

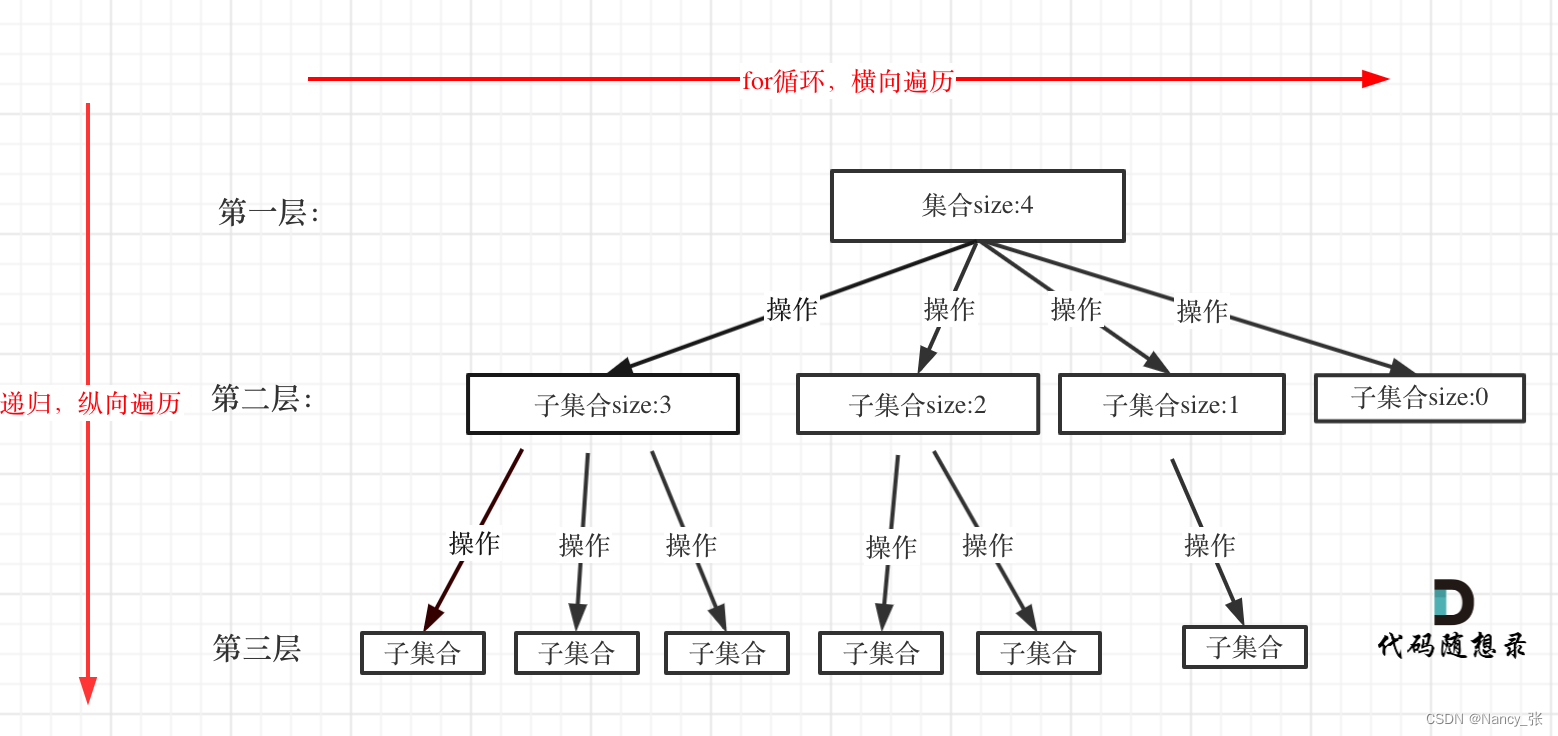
如果对图形困惑的话，请到下方的leetcode题解下结合理解

Part II: 相关题目

Leetcode 77. 组合

解决问题：给定n, k从而确定组合，如n=3, k=2,则组合为[[1,2], [1,3], [2,3]] （组合问题是取出一组，比如封神选六个帅哥当质子团；排列问题是按顺序排成一列，比如质子团按武力值排名，每个月都要打一次架决定最强的）
算法描述：利用回溯算法去确定组合，使得算法复杂度为O(n)=(n-k+1)!（百度组合、排列的计算公式即可知），
算法难点：对我来说是熟悉这个回溯算法的代码模板啦。
代码：

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        # 利用回溯法解决组合问题
        res=[]
        path=[]
        # 通过回溯改变res的值
        self.backtracking(n,k,1,path,res)    
        return res

    # 回溯算法代码
    def backtracking(self,n,k,start,path,res):
        # 设置终止条件，如果一旦取数k个则将组合path添加到组合集res中
        # 注意，这里添加必须是path[:]而不能是path，否则会报错，换成深拷贝也可以
        if len(path)==k:
            res.append(path[:])
            return
        #单层处理逻辑，这里必须使用start,n+1,比如range(1,4+1)才会最终遍历到4
        # n+1可以升级为n-(k-len(path))+2进行剪枝,比如n=50,k=4，则当i=48时，则结束循环
        for i in range(start,n+1):
        	# 将新结果加入path
            path.append(i)
            # 回溯-递归过程
            self.backtracking(n,k,i+1,path,res)
            # 回溯-将新结果弹出
            path.pop()
        # 一般回溯不返回结果
        return