题目链接

Leetcode.1559 二维网格图中探测环 rating : 1838

题目描述

给你一个二维字符网格数组 $grid$ ，大小为 m x n ，你需要检查 $grid$ 中是否存在 相同值 形成的环。

一个环是一条开始和结束于同一个格子的长度 大于等于 $4$ 的路径。对于一个给定的格子，你可以移动到它上、下、左、右四个方向相邻的格子之一，可以移动的前提是这两个格子有 相同的值 。

同时，你也不能回到上一次移动时所在的格子。比方说，环 $(1,1)->(1,2)->(1,1)$ 是不合法的，因为从 $(1,2)$ 移动到 $(1,1)$ 回到了上一次移动时的格子。

如果 $grid$ 中有相同值形成的环，请你返回 true ，否则返回 false 。

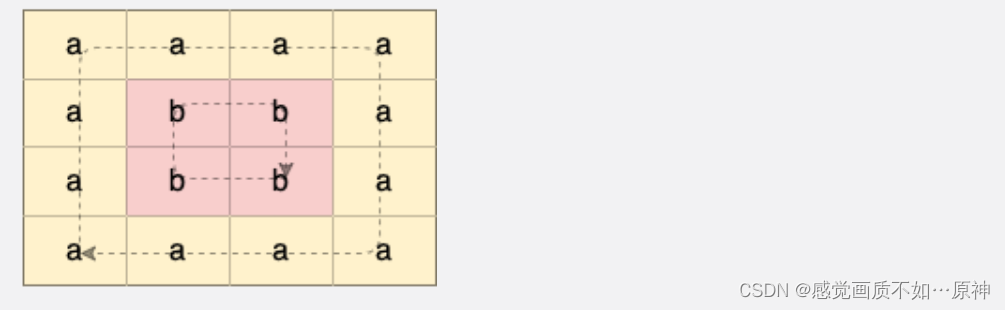
示例 1：

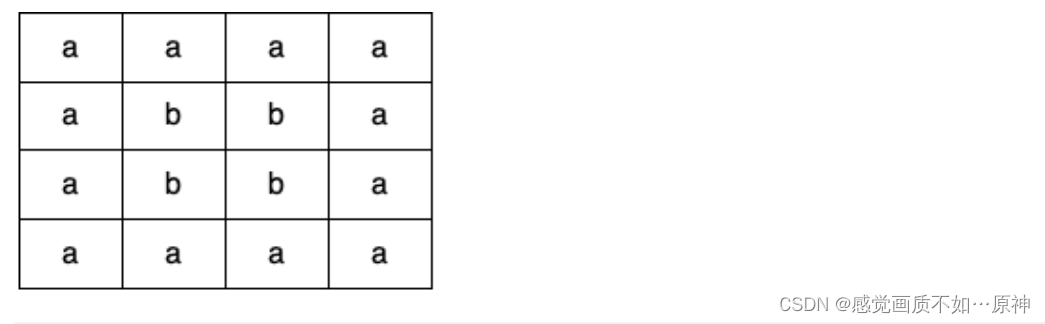
输入：grid = [[“a”,“a”,“a”,“a”],[“a”,“b”,“b”,“a”],[“a”,“b”,“b”,“a”],[“a”,“a”,“a”,“a”]]
输出：true
解释：如下图所示，有 2 个用不同颜色标出来的环：

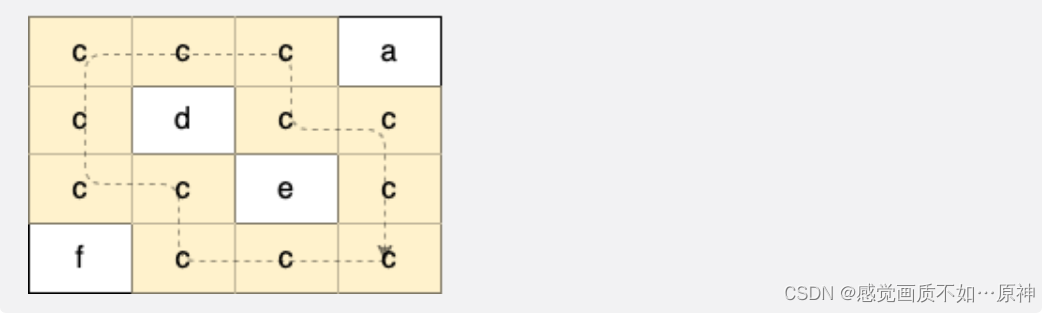
示例 2：

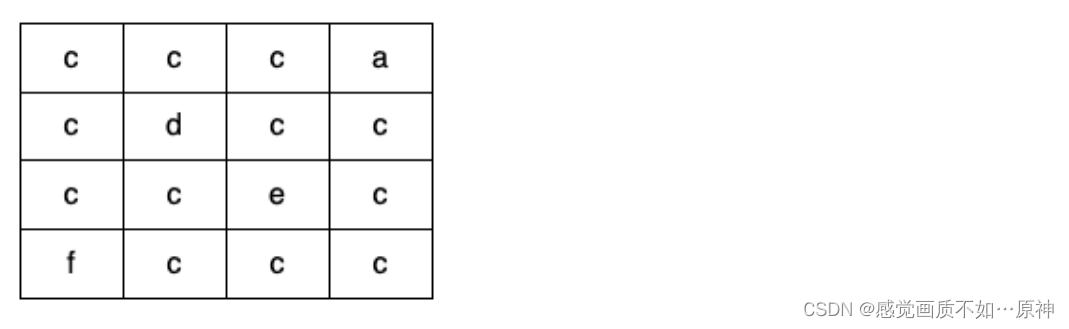
输入：grid = [[“c”,“c”,“c”,“a”],[“c”,“d”,“c”,“c”],[“c”,“c”,“e”,“c”],[“f”,“c”,“c”,“c”]]
输出：true
解释：如下图所示，只有高亮所示的一个合法环：

示例 3：

输入：grid = [[“a”,“b”,“b”],[“b”,“z”,“b”],[“b”,“b”,“a”]]
输出：false

提示：

• $m=grid.length$
• $n=grid[i].length$
• $1\le m\le 500$
• $1\le n\le 500$
• $grid$ 只包含小写英文字母。

解法一：并查集

我们从左上角开始遍历，假设当前位置是 $(i,j)$，我们只用判断它的右边 和 下面的位置即 $(i+1,j)$ 和 $(i,j+1)$。

如果 $grid[i][j]=grid[i+1][j]$ ：

• $grid[i][j]$ 和 $grid[i+1][j]$ 处于两个连通块，那么我就他们合并到一起；
• 如果 $grid[i][j]$ 和 $grid[i+1][j]$ 已经处于同一个连通块了，那么说明存在环，直接返回 true；

如果 $grid[i][j]=grid[i][j+1]$ ：

• $grid[i][j]$ 和 $grid[i][j+1]$ 处于两个连通块，那么我就他们合并到一起；
• 如果 $grid[i][j]$ 和 $grid[i][j+1]$ 已经处于同一个连通块了，那么说明存在环，直接返回 true；

时间复杂度：$O(m\times n)$

C++代码：

class Solution {
public:
    bool containsCycle(vector<vector<char>>& grid) {
        int m = grid.size() , n = grid[0].size() , len = m * n;
        vector<int> p(len);

        for(int i = 0;i < len;i++) p[i] = i;

        function<int(int)> find = [&](int x) -> int{
            if(x != p[x]){
                p[x] = find(p[x]);
            }
            return p[x];
        };

        auto is_connected = [&](int a,int b){
            int x = find(a) , y = find(b);
            if(x == y) return true;
            return false;
        };

        auto merge = [&](int a,int b){
            int x = find(a) , y = find(b);
            p[x] = y;
        };

        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                int x = i * n + j , y;

                if(j + 1 < n && grid[i][j] == grid[i][j + 1]){
                    y = i * n + j + 1;
                    if(is_connected(x,y)) return true;
                    merge(x,y);
                }

                if(i + 1 < m && grid[i][j] == grid[i + 1][j]){
                    y = (i + 1) * n + j;
                    if(is_connected(x,y)) return true;
                    merge(x,y);
                }
            }
        }
        return false;
    }
};

解法二：dfs

我们每次从没有访问过的位置出发开始超 上下左右 四个方向开始访问。

访问的时候注意，不能沿着来的方向再反方向回去。

在 dfs 的过程中，如果我们访问到了跟当前位置值相同，并且之前访问过的点，就说明存在环，直接返回 true。

否则说明不存在环，最后返回 false。

时间复杂度：$O(m\times n)$

C++代码：

//(-1,0) (0,-1) (0,1) (1,0) 分别为 上左右下
//这样对于 k 那么它的反方向就是 3 - k

const int dx[4] = {-1,0,0,1};
const int dy[4] = {0,-1,1,0};
class Solution {
public:
    bool containsCycle(vector<vector<char>>& grid) {
        int m = grid.size() , n = grid[0].size();

        bool vis[m][n];
        memset(vis,false,sizeof vis);

        function<bool(int,int,int)> dfs = [&](int x,int y,int dir) ->bool{
            for(int k = 0;k < 4;k++){
                int nx = x + dx[k] , ny = y + dy[k];
                //dir == k 说明现在的方向 跟 来的时候的方向 相反
                //我们不能再沿着来的路回去，所以这里直接跳过
                if(dir == k || nx < 0 || nx >= m || ny < 0 || ny >= n || grid[x][y] != grid[nx][ny]) continue;
                //此时 (nx,ny) 这个点之前已经访问过了 说明存在环 直接返回true
                if(vis[nx][ny]) return true;
                vis[nx][ny] = true;

                if(dfs(nx,ny,3 - k)) return true;
            }

            return false;
        };

        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                if(vis[i][j]) continue;
                vis[i][j] = true;
                if(dfs(i,j,-1)) return true;
            }
        }

        return false;
    }
};