1 核心思想

论文：Document Dewarping with Control Points
代码：https://github.com/gwxie/document-dewarping-with-control-points
一种通过估计控制点和参考点来纠正失真文档图像的简单而有效的方法。
控制点和参考点由相同数量的顶点组成，分别描述矫正前后图像中文档的形状。 控制点是可控的，以便于交互或后续调整。 您可以根据不同的应用场景，灵活选择后处理方式和顶点数量。

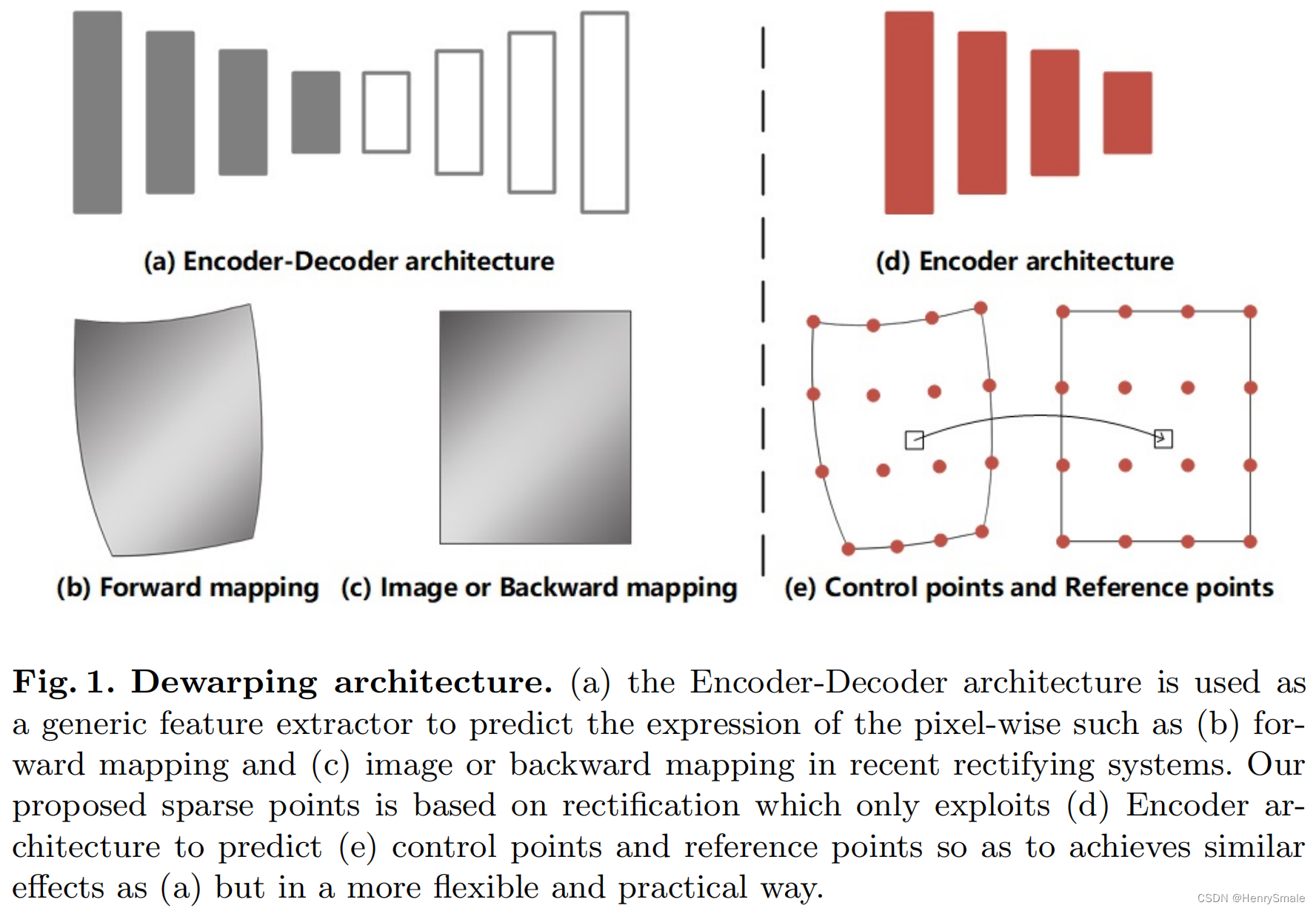
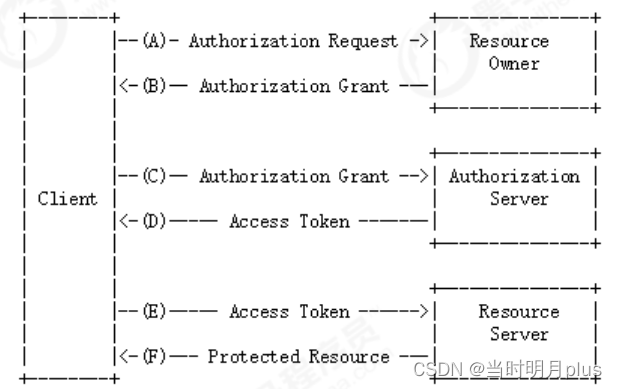
图1所示。去扭曲变形架构。(a) 编码器-解码器架构被用作通用特征提取器来预测像素级的表达式，如(b)正向映射和©最近校正系统中的图像或反向映射。我们提出的稀疏点是基于仅利用的纠正。(d) 编码器架构来预测(e)控制点和参考点，从而以更灵活和实用的方式达到与(a)类似的效果。

本文提出了一种校正失真文档图像并精细去除背景的新方法。如图1(d)所示，我们利用编码器架构从图像中自动提取语义信息，用于预测图1(e)中的控制点和参考点。控制点和参考点由相同数量的顶点组成，分别描述了校正前和校正后文档在图像中的形状。然后，利用控制点与参考点之间的插值方法，将稀疏映射转换为反向映射，并将原始失真文档图像重新映射为校正后的图像。控制点灵活可控，便于与人互动调整次优点。实验表明，基于控制点的方法可以校正各种变形的文档图像，并在真实数据集上取得了较好的效果。此外，我们的方法可以在修正效果不理想的情况下进行多次编辑，提高了其实用性，从而缓解了端到端方法可操作性差的缺点。我们可以根据不同的应用场景灵活选择后处理方法和顶点数量。与像素级回归方法相比，控制点方法更加实用和高效。为了启发今后在这一方向上的研究，我们还提供了一个新的基于控制点的去扭曲变形文档数据集。

2 方法详细描述

2.1 定义

以往的研究将几何校正任务视为密集网格预测问题，将二维图像作为输入，输出一个正向映射(每个网格表示出扭曲输出图像中像素点的坐标，像素点对应出扭曲输入图像中的像素点)或反向映射(每个网格表示出扭曲输入图像中像素点的坐标)。我们的方法简化了这一过程，直接预测稀疏映射，然后使用插值将其转换为密集向后映射。
为了便于解释，我们定义以下概念:
顶点 表示文档图像中某个点的坐标。在本文中，我们可以通过改变坐标来移动顶点。
控制点 由一组顶点组成。如图2©所示，在失真图像上分布控制点，用以描述文档的几何变形。
参考点 由与控制点相同数量的顶点组成。如图2(d)所示，参考点描述规则形状。通过对控制点和参考点进行匹配，利用解翘曲网格实现文档的去翘曲。

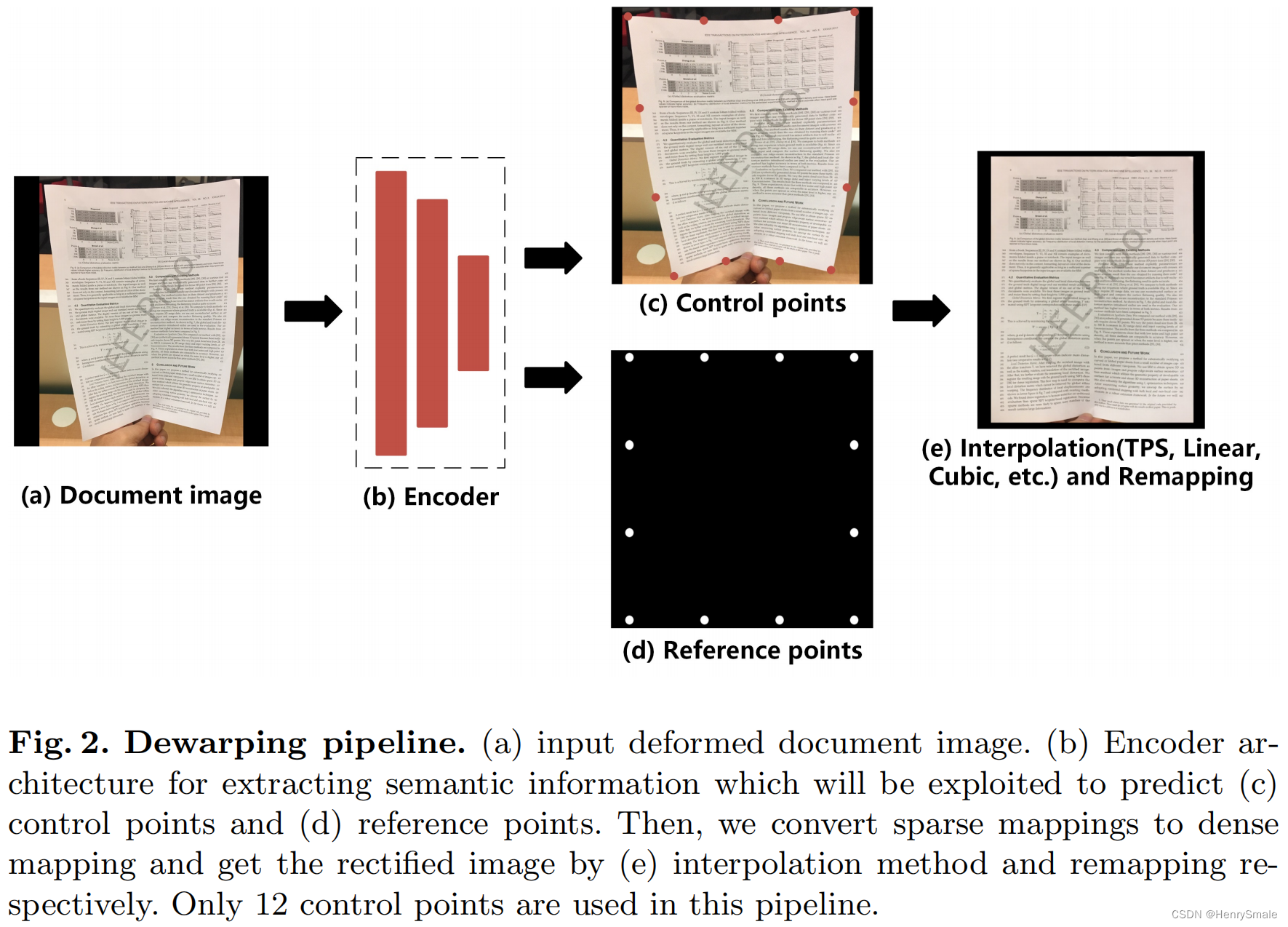
图2所示。去扭曲变形管道。(a)输入变形的文件图像。(b)用于提取语义信息的编码器结构，这些语义信息将被用于预测©控制点和(d)参考点。然后，将稀疏映射转换为密集映射，分别通过(e)插值法和重映射法得到矫正后的图像。在这个管道中只使用了12个控制点。

2.2 去扭曲过程

图2展示了我们工作中的流程。首先，将变形文档的图像输入网络，得到两个输出分支;该方法采用编码器结构作为特征提取器，利用学习到的特征分别预测控制点和参考点，实现多任务预测。其次，如图1(e)所示，我们通过将控制点移动到参考点的位置并将其转换为像素级位置映射来构建矫正网格。为了移动控制点的位置，将稀疏映射转换为密集映射，我们在控制点和参考点之间采用了插值方法[11](TPS, Linear, Cubic等)。之后，从原始扭曲文档图像的一个地方提取像素，并映射到矫正图像的另一个位置。与以往基于DNN的方法相比，我们的方法简单易行。

2.3 网络体系结构

如图2和图3所示，我们的方法以扭曲变形文档图像为输入，预测控制点${\mathbb{R}}^{31\times 31\times 2}$和参考点${\mathbb{R}}^{31\times 31\times 2}$。控制点由$31\times 31$个坐标组成，以匹配相同数量的参考点，从而构建矫正网格。由于参考点是由一个规则网格组成的，它们可以由水平方向和垂直方向$\left(\begin{array}{l}{v}^{\prime }\\ h^{\prime }\end{array}\right)$之间的点的间隔来构造。

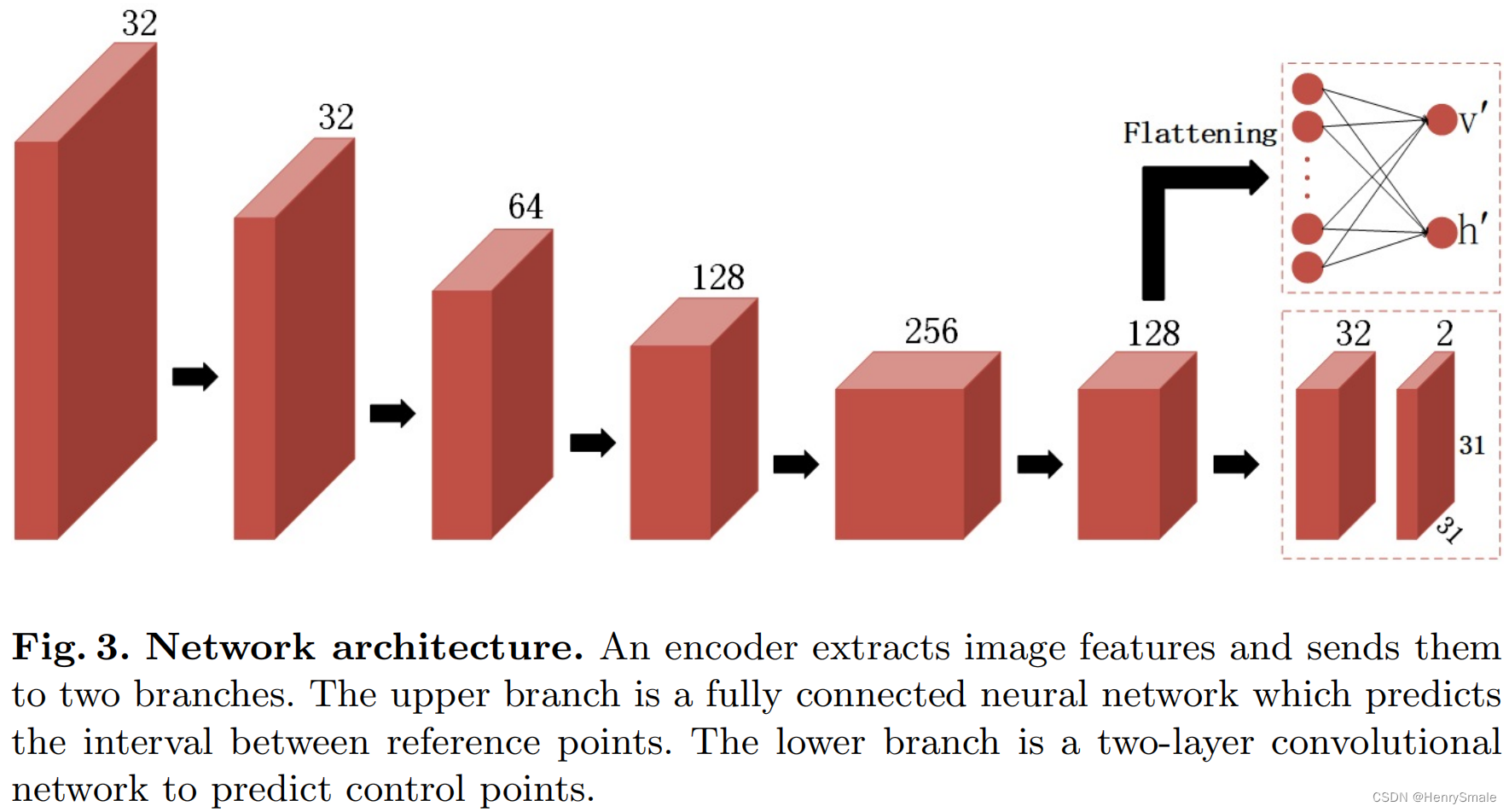
图3 网络体系结构。编码器提取图像特征并将其发送到两个分支。上面的分支是一个完全连接的神经网络，它预测参考点之间的间隔。下层分支是用于预测控制点的两层卷积网络。

在我们的网络中，编码器的前两层使用两个卷积层，其步幅为$2$和$3x3$内核。受[21]架构的启发，我们在编码器架构中使用了相同的结构，包括膨胀残差块和具有堆叠膨胀卷积的空间金字塔。每次卷积后，应用批处理归一化和ReLU。然后，我们将最后一层的特征平坦化，并将其馈送到全连接网络中来预测间隔$\left(\begin{array}{l}{v}^{\prime }\\ h^{\prime }\end{array}\right)$。同时，我们使用两层卷积网络预测控制点${\mathbb{R}}^{31\times 31\times 2}$，在第一次卷积后应用批处理归一化和PReLU。

2.4 训练损失函数

我们使用综合参考点和控制点作为基本真理，以监督的方式训练我们的模型。训练损失函数由两部分组成。一个用于回归点的位置，另一个是两个点在水平和垂直方向上的间隔。
平滑L1损失[7,13]用于控制点的位置回归，对异常值不太敏感。它的定义为:
$$z_i=\{\begin{array}{ll}0.5{\left(p_i-{\hat{p}}_i\right)}^2,& \text{ if }\left|p_i-{\hat{p}}_i\right|<1\\ \left|p_i-{\hat{p}}_i\right|-0.5,& \text{ otherwise }\end{array}\text{\hspace{1em}(1)}$$
$$L_{smoothL1}=\frac{1}{N_c}\sum _i^{N_c}{z}_i\text{\hspace{1em}(2)}$$
$N_c$为控制点的个数，$p_i$和${\hat{p}}_i$分别表示真实的和预测的二维网格中的位置。

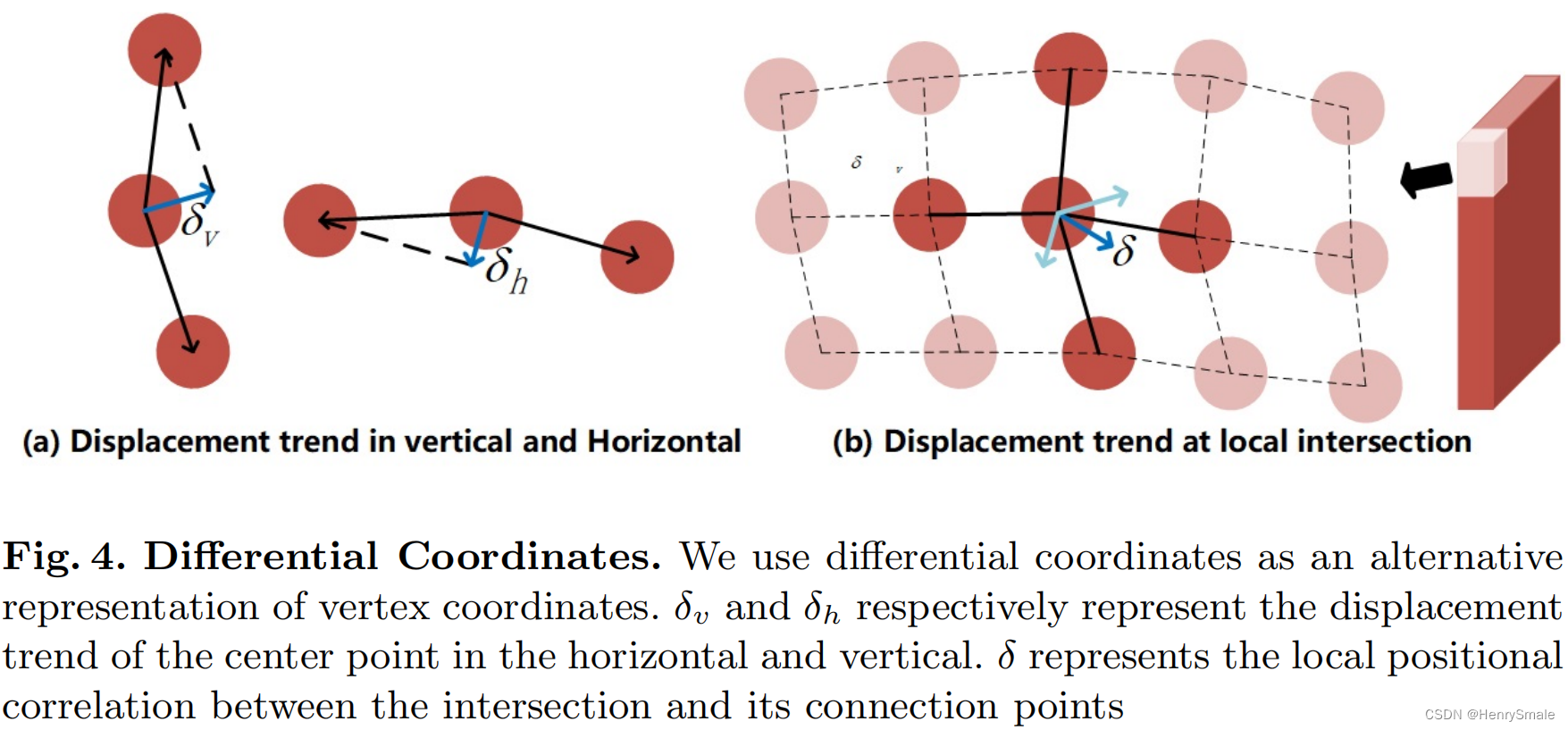
图4 微分坐标。我们使用微分坐标作为顶点坐标的另一种表示。${\delta }_v$和${\delta }_h$分别代表中心点在水平和垂直方向上的位移趋势。$\delta$表示交点与其连接点之间的局部位置相关性。

与人脸重点检测不同，文档图像的内容布局是不规则的。虽然平滑L1损失指导模型如何将每个顶点放置在一个近似的位置，但很难表示一个点相对于它的邻居或每个表面点的局部细节的关系。为了建立一个容错能力更强的模型来更好地描述形状，我们使用微分坐标作为中心坐标的替代表示。如图4所示，${\delta }_v$和${\delta }_h$分别代表中心点在水平和垂直方向上的位移趋势，有助于保持相应方向上的相关性。同理，$\delta$表示交叉口与两个方向的局部位置相关性，可定义为:
$$\delta =\sum _{j=1}^k\left(p_j-p_i\right)\text{\hspace{1em}(3)}$$