期权定价模型系列【1】—BSM通用式模型

这是期权定价模型专栏的第一篇文章，此专栏旨在分享一些期权定价模型，将会从最基础的BSM模型开始写起，逐步扩散到蒙特卡洛模拟、二叉树等数值法模型，以及跳跃扩散模型、随机波动率模型，神经网络模型等等。

如果你觉得有帮助，不妨点赞收藏支持一下哦。

1.前言

1973年BSM模型首次发表后便很快被应用到了金融市场中。交易商用BSM模型对期权进行定价，并进一步推动了期权在不同市场上的应用。自BSM模型开始，市场首次找到了理论上可靠的期权定价模型，这大大推动了整个期权市场的发展，反过来也促进了标的资产市场的定价和流动性。
在某种意义上，BSM模型确实是个奇迹：它使得你可以用一种非常理性的方法来给证券定价，在此之前，根本没有一个合理的或者站得住脚的定价理论。一个完全理想化的世界中（假设回报服从正态分布，股票价格服从几何布朗运动规律，具有充沛的流动性，可以进行持续套期保值，并且没有交易成本），BSM模型提供了一种动态复制期权的方法。这是一个在想象世界中工程学方法所创造的杰作，只是这个世界并不存在，因为市场并不总是服从所有的假设条件。这确实是个奇迹，但是它也只是一个模型，并不是实际情况。

当然，BSM模型所要求的假设条件非常严苛：假设标的资产的回报服从正态分布、价格服从几何布朗运动、市场始终可以提供充沛的流动性、可以进行无成本的连续对冲交易等。在真实的市场中，这些假设条件有一些可以近似满足，还有一些就相距甚远。比如，交易成本和连续对冲，可以通过调整假设条件来实现。还有一些，比如股票价格变动的模式，就很难服从几何布朗运动的假设。在现实中，股票价格经常会出现跳跃，整体分布呈现肥尾，甚至波动率也会出现完全无法预计的变动，这些条件就很难通过调整假设条件来解决。

2.静态复制

首先，通过期权定义可以很容易得到一个普通欧式看涨期权与看跌期权在到期日的合约价值为：

那么，假设投资者买入一个欧式看涨期权，同时卖出一个行权价相同的欧式看跌期权，那么无论到期日股票的最终价格是多少，投资者能获得收益都是确定的：（ST-K）。

更进一步，假设股票在未来没有分红。在到期日之前的某个时间t，如果投资者按照当前价格St买入一份标的股票，同时卖出Ke-r（T-t）份无风险债券，那么在T时刻，这个组合的价值就是（ST-K）。根据一价定律可知，一个是买入欧式看涨期权，同时卖出行权价相等的欧式看跌期权，一个是买入股票，同时卖出无风险债券，这两者当前的价格应该是相等的，即为：

通过对上式两边进行移项，要复制一个看涨期权只需要一个行权价和到期日都相同的看跌期权、标的股票以及无风险债券。要复制一个看跌期权，只需要一个行权价格和到期日都相同的看涨期权、标的股票以及无风险债券

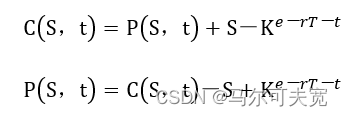
3.模型推导

运用复制的方法进行估值是整个布莱克-斯科尔斯-默顿（BSM）期权定价模型的理论基础。在推导BSM模型的时候，需要进行一系列的理论假设：标的股票价格的变化是连续的，波动率为常数并且没有价格跳跃（单因子布朗运动）；交易员可以通过大额多头或空头头寸进行持续对冲；没有买卖差价；没有交易成本；可以自主决定头寸调整。

假设在t时刻，某股票的价格为S，其波动率为常数σS，预期回报为μS。同时，还存在一只无风险债券，其价格为B，收益率假设为常数r。股票和债券的随机价格服从：

其中，dZ服从标准维纳过程。以该股票为标的资产的看涨期权在t时刻的价格C，是一个跟股票价格和时间相关的变量。根据伊藤引理，C的价格等于：

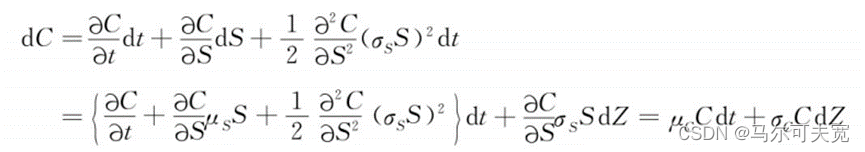
其中有：

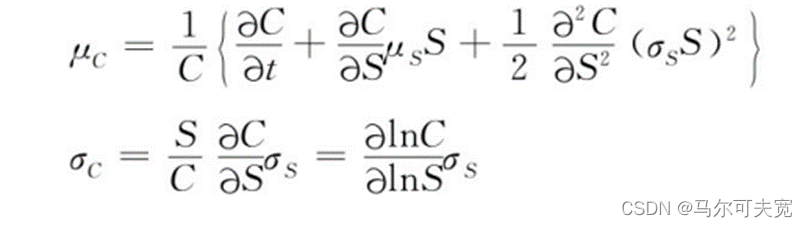
将S和C的头寸结合在一起，构建一个持续的无风险组合，消除该风险变量。令π=αS+C，其中α表示在t时刻对冲期权风险所需的股票数量。那么就有：

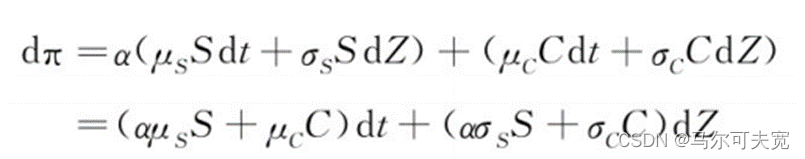
要使这个组合保持瞬时无风险，随机变量dZ的协方差就必须要等于0。也就是：

其中：

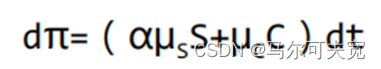
由于这个组合在t时刻也是无风险的，根据一价定律，在t时刻其收益率也应该是无风险利率r，所以就有：

在对冲组合中，这相当于：

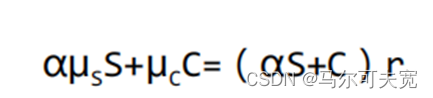
进行移项调整后有：

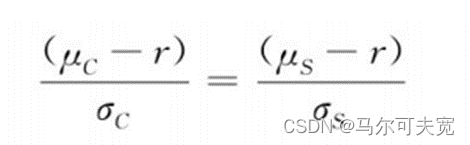
看涨期权和标的股票的瞬时夏普比率相等。如果不存在无风险套利的机会，那么对股票和期权来说，每单位波动率对应的超额回报是相等的。这也是布莱克和斯科尔斯最开始在推导BSM等式时提出的观点。继续进行计算，替换μC和σC有：

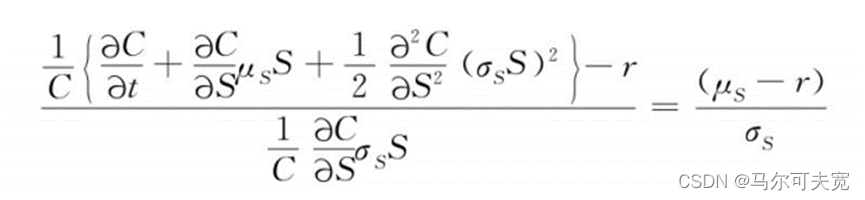
可得BSM模型的偏微分方程式：

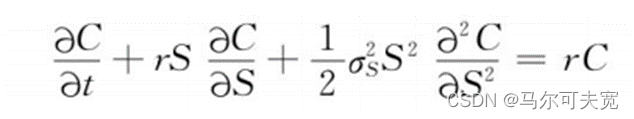
4.BSM模型

BSM模型是由Black和Scholes推导出来的可以被用于到期前不分红的欧式股票期权的估值模型，假定c和p分为代表欧式看涨与欧式看跌期权的价格，则期权的定价公式为：

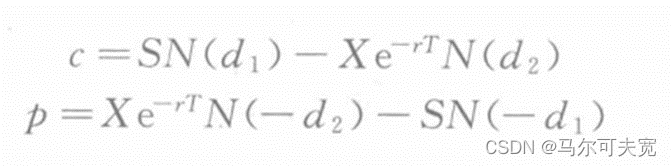
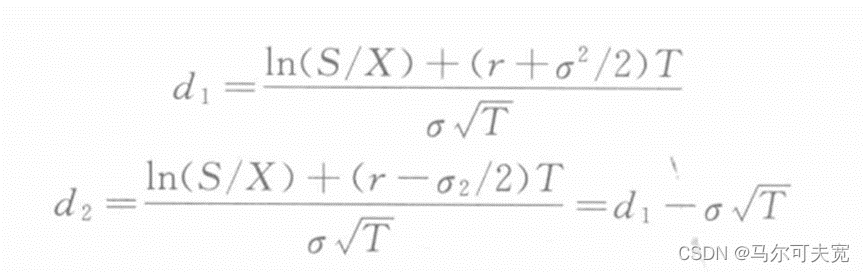
参数释义如下：

5.股指期权定价模型

Merton将BS模型扩展到允许支付连续股息的情景，这一模型可以用于支付已知连续股息率q的股票或者股指的欧式看涨、欧式看跌期权的定价问题。

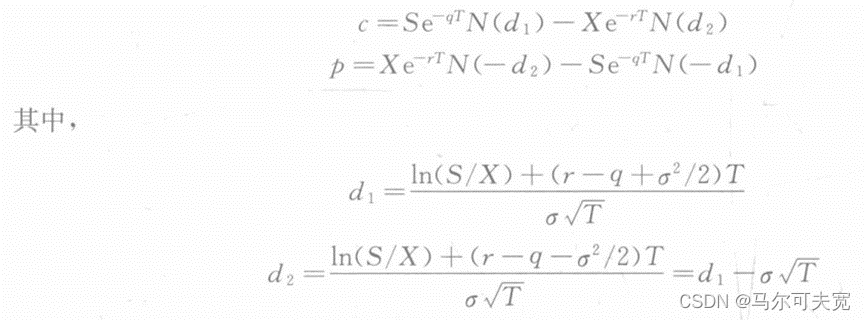
6.期货期权定价模型

Black在1976年给出了用于为标的资产为远期或者期货合约定价的欧式看涨、欧式看跌期权定价模型，假设标的资产价格为F。

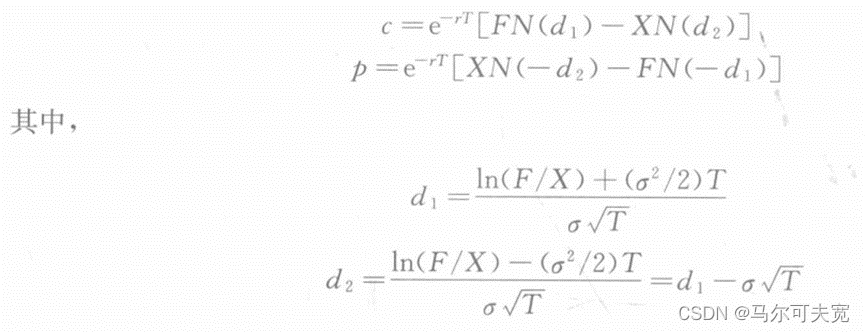
7.权利金计息的期货期权定价模型

Asay修改了权利金计息的Black76期货期权定价模型：

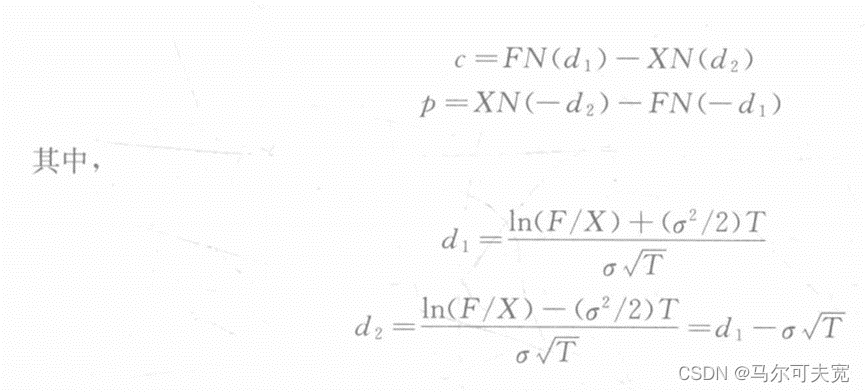
8.外汇期权定价模型

Garman和Kohlhagen修改了BS模型，使之可以用于欧式外汇期权的定价：

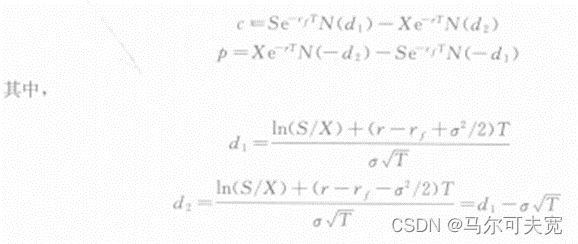
9.广义的BSM期权定价模型

如果引入一个持有成本率b，则BSM模型能够被一般化，这个模型可以用于定价标的为无股息股票、连续支付股息的股票、期货、外汇的欧式期权：

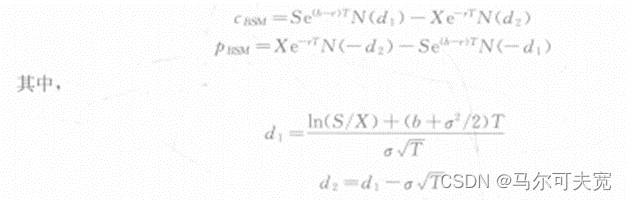
b=r时为1973年提出的无股息欧式期权定价模型；

b=r-q时为merton在1973年提出的连续股利欧式期权定价模型；

b=0时为black在1976年提出的期货期权定价模型；

b=0且r=0时为Asay在1982年提出的权利金计息下的期货期权定价模型；

b=r-rf时为外汇期权定价模型。

10.代码部分

import numpy as np
from scipy.stats import norm

class BSM_Model:

    def __init__(self,S,K,T,sigma,r,b,opt):
        self.S=S
        self.K=K
        self.T=T
        self.sigma=sigma
        self.r=r
        self.b=b
        self.opt=opt

    def d1(self):
        return (np.log(self.S/self.K)+(self.b+self.sigma**2/2)*self.T)/(self.sigma*np.sqrt(self.T))
    def d2(self):
        return self.d1()-self.sigma*np.sqrt(self.T)

    def option_value(self):
        if self.opt=='call':
            value=self.S*np.exp((self.b-self.r)*self.T)*norm.cdf(self.d1())-self.K*np.exp(-self.r*self.T)*norm.cdf(self.d2())
        else:
            value = -self.S * np.exp((self.b - self.r) * self.T) * norm.cdf(-self.d1()) + self.K * np.exp(
                -self.r * self.T) * norm.cdf(-self.d2())
        return value

例1：

结果为：欧式看涨期权价格为2.1333684449162007

if __name__=='__main__':
    #b=r时为1973年提出的无股息欧式期权定价模型
    # eg：
    S=60
    K=65
    T=0.25
    r=0.08
    sigma=0.3
    b=r
    opt='call'
    call=BSM_Model(S,K,T,sigma,r,b,opt).option_value()
    print('欧式看涨期权价格为%s'%(call))

例2：

结果为：欧式看跌期权价格为2.4647876467558305

if __name__=='__main__':
    #b=r-q时为merton在1973年提出的连续股利欧式期权定价模型
    S=100
    K=95
    T=0.5
    r=0.1
    q=0.05
    sigma=0.2
    b=r-q
    opt='put'
    put=BSM_Model(S,K,T,sigma,r,b,opt).option_value()
    print('欧式看跌期权价格为%s'%(put))

例3：

结果为：看跌期货期权价格为1.7010507252362679

if __name__=='__main__':

    #b=0时为black在1976年提出的期货期权定价模型
    F = 19
    K = 19
    T = 0.75
    r = 0.1
    sigma = 0.28
    b = 0
    opt = 'put'
    put = BSM_Model(F, K, T, sigma, r, b, opt).option_value()
    print('看跌期货期权价格为%s' % (put))

例4：

结果为：看跌期货期权价格为65.61854211535751

if __name__=='__main__':

   
    #b=0且r=0时为Asay在1982年提出的权利金计息下的期货期权定价模型
    F = 4200
    K = 3800
    T = 0.75
    r =0
    sigma = 0.15
    b = 0
    opt = 'put'
    put = BSM_Model(F, K, T, sigma, r, b, opt).option_value()
    print('看跌期货期权价格为%s' % (put))

例5：

结果为：看涨外汇权价格为0.02909925314943973

if __name__=='__main__':
    #b=r-rf时为外汇期权定价模型
    S = 1.56
    K = 1.6
    T = 0.5
    r = 0.06
    rf=0.08
    sigma = 0.12
    b = r-rf
    opt = 'call'
    call = BSM_Model(S, K, T, sigma, r, b, opt).option_value()
    print('看涨外汇权价格为%s' % (call))