openssl安装问题合辑
news2026/2/11 17:23:19
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/854848.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
【ARM Cache 系列文章 9 -- ARM big.LITTLE技术】
文章目录 big.LITTLE 技术背景big.LITTLE 技术详解big.LITTLE 硬件要求 big.LITTLE 软件模型CPU MigrationGlobal Task SchedulingGlobal Task Scheduling比CPU Migration的优势 转自:https://zhuanlan.zhihu.com/p/630981648 如有侵权,请联系删除 big.L…
Codeforces Round 889 (Div. 2)C题题解
文章目录 [Dual (Hard Version)](https://codeforces.com/contest/1855/problem/C2)问题建模问题分析1.按元素值分类讨论,正负不同时存在时2.若正负同时存在时代码 Dual (Hard Version) 问题建模
给定n个数,n不超过20,且每个数ai,…
MachineLearningWu_14/P65-P69_Multiclass
x.1 Multiclass多分类问题
对于分类问题,往往指的是二分类问题,而对于二分类的decision boundary较为简单,而实际生活中会有很多问题是多分类问题,例如MNIST手写数字识别, 从特征空间上来看,二分类和多分类…
【C++】开源:ncurses终端TUI文本界面库
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍ncurses终端文本界面库。 无专精则不能成,无涉猎则不能通。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,下…
OpenCV基础知识4 — 绘制图形
前言:Hello大家好,我是小哥谈。Opencv提供了许多用于绘制图形的方法,包括绘制线段的line()方法、绘制矩形的retangle()方法、绘制圆形的circle()方法、绘制多边形的polylines()方法和绘制文字的putText()方法。本节课将依次对上述各个方法进行…
【JPCS出版】第五届能源、电力与电网国际学术会议(ICEPG 2023)
第五届能源、电力与电网国际学术会议(ICEPG 2023)
2023 5th International Conference on Energy, Power and Grid
最近几年,不少代表委员把目光投向能源电力领域,对促进新能源发电产业健康发展、电力绿色低碳发展,提…
【动态内存管理助力程序优化与性能飞升】
本章重点 为什么存在动态内存分配 动态内存函数的介绍 malloc free calloc realloc 常见的动态内存错误 几个经典的笔试题 柔性数组 1. 为什么存在动态内存分配
我们已经掌握的内存开辟方式有:
int val 20;//在栈空间上开辟四个字节
char arr[10] {0};//在栈…
R语言中的函数24:Combinat:combn(), permn()
介绍
combinat中的combn()和permn()函数可以得到所有的排列组合的情况
combn()函数
combn(x, m, funNULL, simplifyTRUE, …)x – 组合的向量源m – 要取的元素的数量fun – 应用于每个组合的函数(可能为空)simplify – 逻辑的,如果是FALSE,返回一个列…
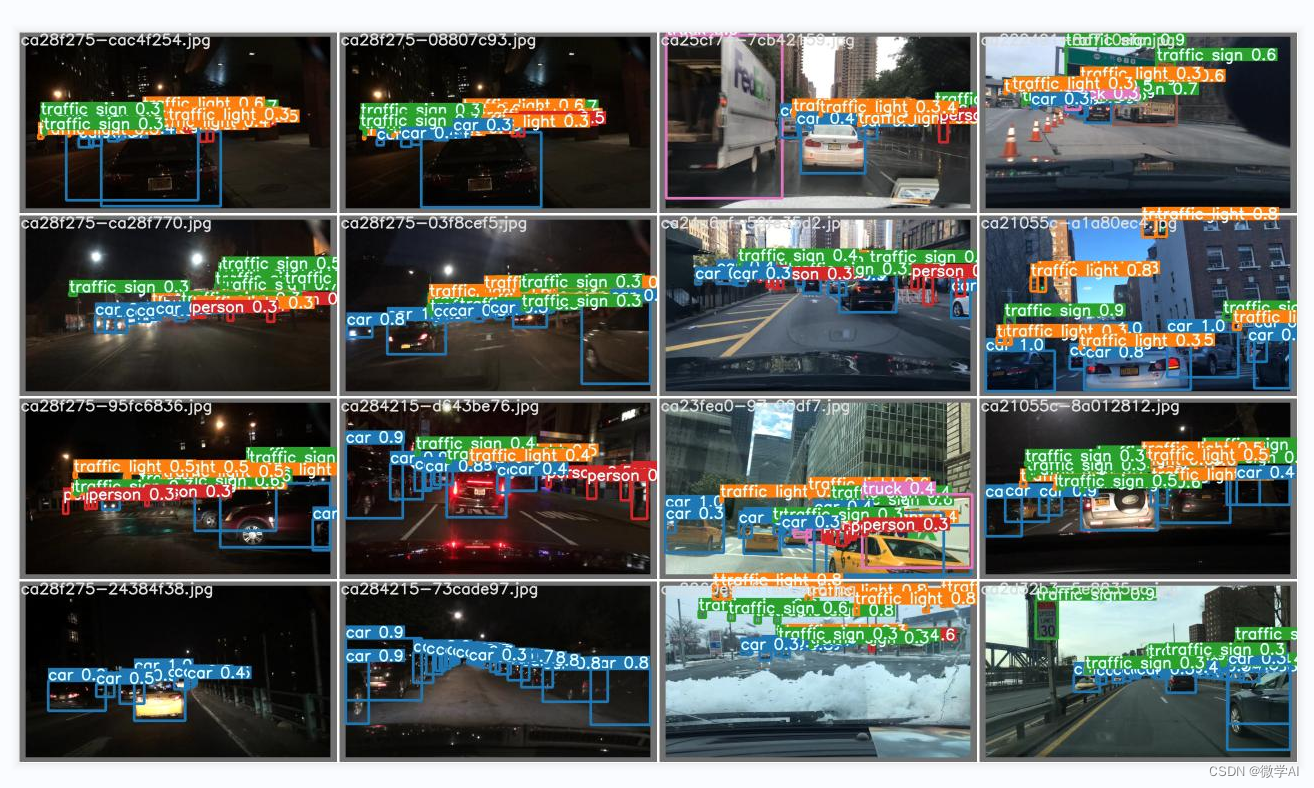
计算机视觉的应用9-视觉领域中的61个经典数据集【大集合】的应用与实战
大家好,我是微学AI,今天给大家介绍一下计算机视觉的应用9-视觉领域中的61个经典数据集【大集合】的应用与实战,我们都知道计算机视觉是一门研究如何使计算机能够理解和解释数字图像或视频的技术和方法。在计算机视觉领域中,数据集是非常重要的资源,它们可以用于训练和评估…
C++(Qt)软件调试---将调试工具安装到AeDebug(11)
C(Qt)软件调试—将调试工具安装到AeDebug(11) 文章目录 C(Qt)软件调试---将调试工具安装到AeDebug(11)1、前言1.1 使用的调试工具 2、调试器安装1.1 WinDbg1.2 procdump1.3 DrMinGW1.4 vsjitdebugger 更多精彩内容👉个…
C++学习| VS配置FFTW3以及一维傅里叶变换的使用
前言:最近要用C对信号进行一维傅里叶变换,但是对傅里叶变换的内容有些遗忘了,同时自己对FFTW使用也不太了解,所以写下此篇方便以后回顾。
VS项目配置FFTW3
FFTW ( the Faster Fourier Transform in the West) 是一个快速计算离散…
STM32 F103C8T6学习笔记2:GPIO的认识—GPIO的基本输入输出—点亮一个LED
今日继续学习使用 STM32 F103C8T6开发板 点亮一个LED灯,文章提供源码,测试工程,实验效果图,希望我的归纳总结会对大家有帮助~
目录
GPIO的认识与分类 :
引脚安排整理:
定时器的引脚例举:
…
openGauss学习笔记-35 openGauss 高级数据管理-ALTER TABLE语句
文章目录 openGauss学习笔记-35 openGauss 高级数据管理-ALTER TABLE语句35.1 语法格式35.2 参数说明35.3 示例 openGauss学习笔记-35 openGauss 高级数据管理-ALTER TABLE语句
修改表,包括修改表的定义、重命名表、重命名表中指定的列、重命名表的约束、设置表的所…
npm 报错 cb() never called!
不知道有没有跟我一样的情况,在使用npm i的时候一直报错:cb() never called!
换了很多个node版本,还是不行,无法解决这个问题
百度也只是让降低node版本请缓存,gpt给出的解决方案也是同样的
但是缓存清过很多次了&a…
Vue自定义指令使用
本篇文章讲述使用Vue自定义指令,并在项目中完成相应功能。
在平常Vue脚手架项目中,使用到 自定义指令较少,一般都是使用的自带指令,比如 v-show 、v-if 、 v-for 、 v-bind 之类的。这些已经能够满足大多数项目使用。更多的可能也…
2462. 雇佣 K 位工人的总代价;948. 令牌放置;1262. 可被三整除的最大和
2462. 雇佣 K 位工人的总代价
核心思想:分情况讨论,当2*candidates > n 时,直接取前k个工人即可;当2*candidates< n时,我们可以维护两个最小堆,然后不断比较堆中的值,然后用i,j两个指针表…
Java项目练习--上
任务一:创建一个简单的银行程序包
目的:Java语言中面向对象的封装及构造器的创建与使用
说明:创建Account类,将源文件放入banking程序包中。在创建单个账户的默认程序包中,已经编写了测试程序TestBanking,这个测试程…
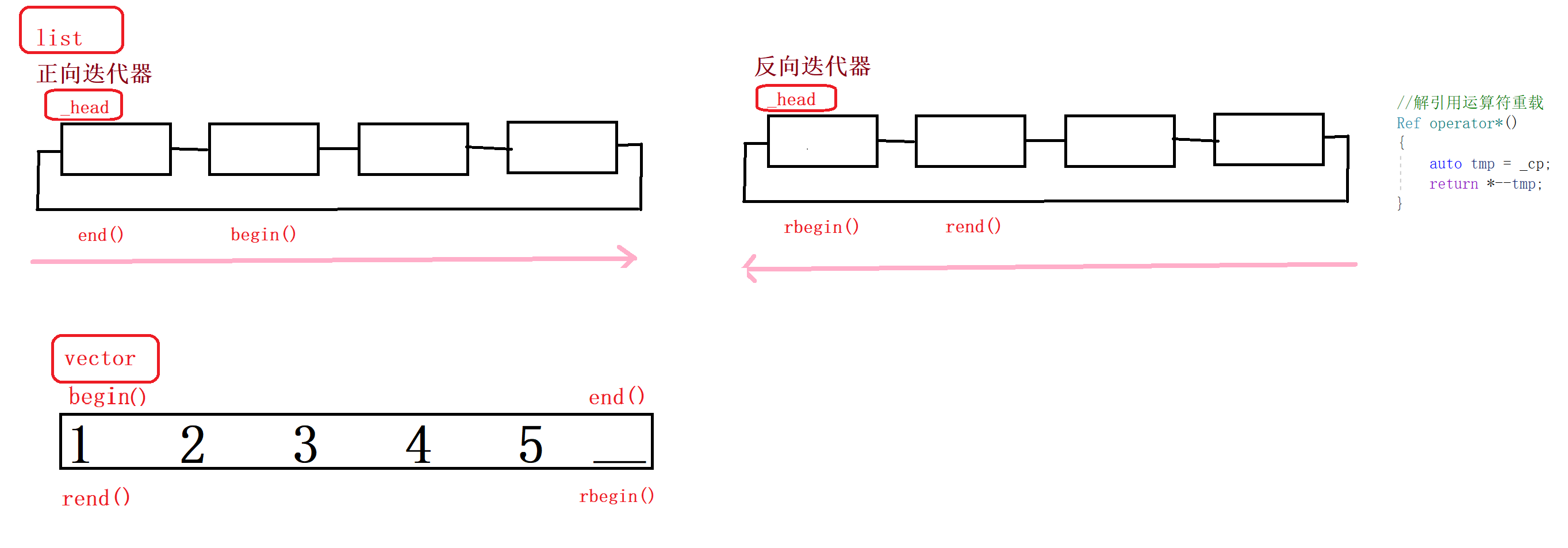
list模拟实现【引入反向迭代器】
文章目录 1.适配器1.1传统意义上的适配器1.2语言里的适配器1.3理解 2.list模拟实现【注意看反向迭代器】2.1 list_frame.h2.2riterator.h2.3list.h2.4 vector.h2.5test.cpp 3.反向迭代器的应用1.使用要求2.迭代器的分类 1.适配器
1.1传统意义上的适配器 1.2语言里的适配器
容…
nginx负载均衡(反向代理)
nginx负载均衡 负载均衡:由反向代理来实现。 nginx的七层代理和四层代理: 七层是最常用的反向代理方式,只能配置在nginx配置文件的http模块当中,而且配置方法名称:upstream模块,不能写在server模块中&#…
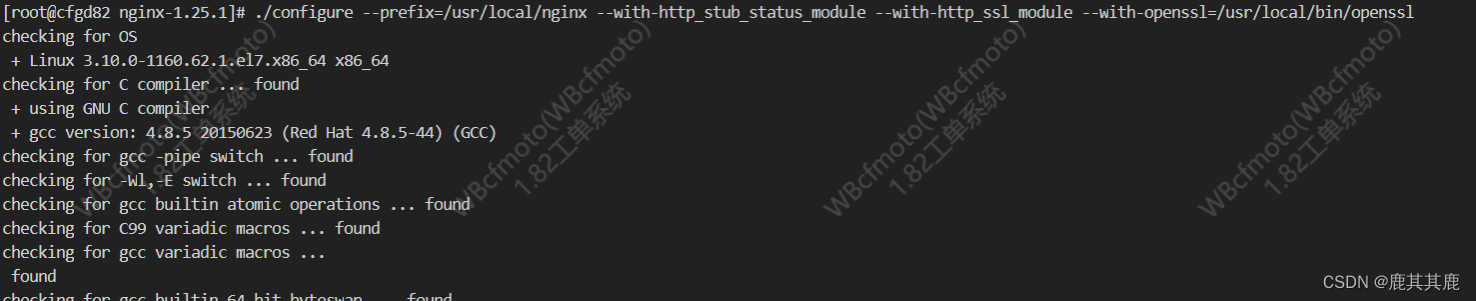

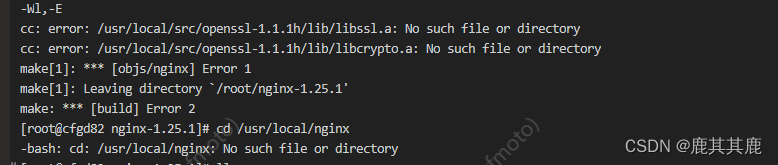
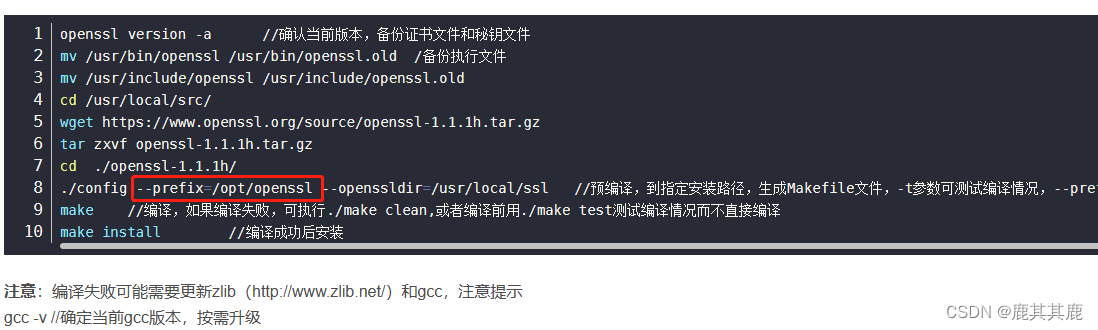 就成功了。
就成功了。