弗洛伊德算法Floyd是针对多源路径找出最短的路径,其中数据结构会使用到前面介绍过的邻接矩阵,有兴趣的可以先查阅:图数据结构之邻接矩阵Adjacency Matrix(Python版) 先了解这个邻接矩阵然后再回看本文章也可以。
区别在于这里我们介绍的是带权值的边,通过两个步骤来思考:
1、创建邻接矩阵,和前面一样也属于对角线(值为0)对称的矩阵,区别在于我们将没有联通的点的边取值为一个比较大的值(比矩阵中的一般权值大且小于最大值避免相加溢出)即可,在很多博客也可能使用无穷大(表示永远到不了,就是没有相连的意思)来表示这个无边的情况,这点需要注意。
2、创建路径矩阵,每次插入一节点k,然后遍历每个点对(i,j双重循环),判断每个点对之间的距离会不会因为插入的点而发生最小路径(距离,权值和)的变化,如果有变小,那么就更新这两点间(i,j)的距离,所以也可以叫做插点法。
其中对于这个插入节点k,可以这么去理解,比如说从湖南到西藏,在此之前都是走A路,后面在中间修了一条路,使得湖南去西藏的路多了起来,其中经过这条新修的路,去西藏的距离变得更短了,那么我们就重新选择这条新的短路径。
了解了原理之后,我们上代码:
# 定义一个比较大的值(表示没有联通,无边)
NoEdgeV = 1000
class FloydGraph():
'''
弗洛伊德算法
创建两个矩阵,一个是带权值的邻接矩阵,另一个是保存权值的路径矩阵
nodes:节点列表
adjacencyMatrix:保存的是点对的距离
pathMatrix:保存路径(索引值)
'''
def __init__(self, nodes, adjacencyMatrix, pathMatrix):
self.nodes = nodes
self.ajd_matrix = adjacencyMatrix
self.node_len = len(adjacencyMatrix)
self.path_matrix = pathMatrix
self._init_Floyd()
def __call__(self, start, end):
self.start = start
self.end = end
return self._format_path()
def _init_Floyd(self):
# 插入k点来判断路径是否需要更新
for k in range(self.node_len):
for i in range(self.node_len):
for j in range(self.node_len):
#self.ajd_matrix[i][j] = min(self.ajd_matrix[i][j], self.ajd_matrix[i][k] + self.ajd_matrix[k][j])
# i到插入点k与插入点k到j的路径之和
tmp = self.ajd_matrix[i][k] + self.ajd_matrix[k][j]
# 如果插入点之后,路径变短了,那就更新这点的值即可
if self.ajd_matrix[i][j] > tmp:
self.ajd_matrix[i][j] = tmp
self.path_matrix[i][j] = self.path_matrix[i][k]
def _format_path(self):
node_list = []
start = self.start
end = self.end
print("%s到%s的最短距离为:%d" % (
self.nodes[self.start], self.nodes[self.end], self.ajd_matrix[start][end]))
node_list.append(self.nodes[start])
while True:
node_list.append(self.nodes[self.path_matrix[start][end]])
start = self.path_matrix[start][end]
if start == end:
break
return node_list
def createTwoMatrix(node_map, nodes, node_list, path_map):
for i in range(len(nodes)):
node_map[i][i] = 0
for n1, n2, val in node_list:
node_map[nodes.index(n1)][nodes.index(n2)] = val
node_map[nodes.index(n2)][nodes.index(n1)] = val
path_map[nodes.index(n1)][nodes.index(n2)] = nodes.index(n2)
path_map[nodes.index(n2)][nodes.index(n1)] = nodes.index(n1)
if __name__ == "__main__":
nodes = ['A', 'B', 'C', 'D', 'E', 'F', 'G']
node_list = [('A', 'F', 2), ('A', 'B', 6), ('A', 'G', 5), ('A', 'C', 5),
('G', 'B', 7), ('B', 'E', 3), ('C', 'B', 1), ('C', 'F', 2), ('E', 'D', 4)]
adjMatrix = [[NoEdgeV for val in range(len(nodes))] for val in range(len(nodes))]
pathMatrix = [[0 for val in range(len(nodes))] for val in range(len(nodes))]
createTwoMatrix(adjMatrix, nodes, node_list, pathMatrix)
i1 = nodes.index('A')
i2 = nodes.index('E')
Floydpath = FloydGraph(nodes, adjMatrix, pathMatrix)
path = Floydpath(i1, i2)
print(path)
'''
A到E的最短距离为:8
['A', 'F', 'C', 'B', 'E']
'''我们来将最短路径可视化,这样看起来更直观一点。先将所有节点设置坐标,然后将获得的最短路径的节点转换成坐标,用来显示节点名称和连线用:
#可视化
all_xy = np.array([[3.5, 4], [5, 4], [2, 3], [4.5, 2], [6, 2], [3, 6], [4.5, 6]])
path_index = [] # 保存节点的索引
for i in range(len(path)):
path_index.append(nodes.index(path[i]))
path_xy = all_xy[path_index] # 转成坐标
#显示所有节点
for i in range(len(all_xy)):
plt.plot(all_xy[i, 0], all_xy[i, 1], color='blue',marker='$'+nodes[i]+'$', markersize=15)
#突出显示最短路径节点名称
for i in range(len(path_xy)):
plt.plot(path_xy[i, 0], path_xy[i, 1], color='red',marker='$'+path[i]+'$', markersize=15)
#最短路径连线
getx = path_xy[:, 0]
gety = path_xy[:, 1]
plt.plot(getx, gety, color='grey', marker='.', markersize=3, linestyle='-.')
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.title("最短路径距离:"+str(adjMatrix[i1][i2]))
plt.show()这块其实就是点线图的使用,全部代码如下:
import numpy as np
import matplotlib.pyplot as plt
# 定义一个比较大的值(表示没有联通,无边)
NoEdgeV = 1000
class FloydGraph():
'''
弗洛伊德算法
创建两个矩阵,一个是带权值的邻接矩阵,另一个是保存权值的路径矩阵
nodes:节点列表
adjacencyMatrix:保存的是点对的距离,会更新成最短
pathMatrix:保存路径(索引值)
'''
def __init__(self, nodes, adjacencyMatrix, pathMatrix):
self.nodes = nodes
self.ajd_matrix = adjacencyMatrix
self.node_len = len(adjacencyMatrix)
self.path_matrix = pathMatrix
self._init_Floyd()
def __call__(self, start, end):
self.start = start
self.end = end
return self._format_path()
def _init_Floyd(self):
# 插入k点来判断路径是否需要更新
for k in range(self.node_len):
for i in range(self.node_len):
for j in range(self.node_len):
#self.ajd_matrix[i][j] = min(self.ajd_matrix[i][j], self.ajd_matrix[i][k] + self.ajd_matrix[k][j])
# i到插入点k与插入点k到j的路径之和
tmp = self.ajd_matrix[i][k] + self.ajd_matrix[k][j]
# 如果插入点之后,路径变短了,那就更新这点的值即可
if self.ajd_matrix[i][j] > tmp:
self.ajd_matrix[i][j] = tmp
self.path_matrix[i][j] = self.path_matrix[i][k]
def _format_path(self):
node_list = []
start = self.start
end = self.end
print("%s到%s的最短距离为:%d" % (
self.nodes[self.start], self.nodes[self.end], self.ajd_matrix[start][end]))
node_list.append(self.nodes[start])
while True:
node_list.append(self.nodes[self.path_matrix[start][end]])
start = self.path_matrix[start][end]
if start == end:
break
return node_list
def createTwoMatrix(node_map, nodes, node_list, path_map):
for i in range(len(nodes)):
node_map[i][i] = 0
for n1, n2, val in node_list:
node_map[nodes.index(n1)][nodes.index(n2)] = val
node_map[nodes.index(n2)][nodes.index(n1)] = val
path_map[nodes.index(n1)][nodes.index(n2)] = nodes.index(n2)
path_map[nodes.index(n2)][nodes.index(n1)] = nodes.index(n1)
if __name__ == "__main__":
nodes = ['A', 'B', 'C', 'D', 'E', 'F', 'G']
node_list = [('A', 'F', 2), ('A', 'B', 6), ('A', 'G', 5), ('A', 'C', 5),
('G', 'B', 7), ('B', 'E', 3), ('C', 'B', 1), ('C', 'F', 2), ('E', 'D', 4)]
adjMatrix = [[NoEdgeV for val in range(len(nodes))] for val in range(len(nodes))]
pathMatrix = [[0 for val in range(len(nodes))] for val in range(len(nodes))]
createTwoMatrix(adjMatrix, nodes, node_list, pathMatrix)
i1 = nodes.index('A')
i2 = nodes.index('E')
Floydpath = FloydGraph(nodes, adjMatrix, pathMatrix)
path = Floydpath(i1, i2)
print(path)
#可视化
all_xy = np.array([[3.5, 4], [5, 4], [2, 3], [4.5, 2], [6, 2], [3, 6], [4.5, 6]])
path_index = [] # 保存节点的索引
for i in range(len(path)):
path_index.append(nodes.index(path[i]))
path_xy = all_xy[path_index] # 转成坐标
#显示所有节点
for i in range(len(all_xy)):
plt.plot(all_xy[i, 0], all_xy[i, 1], color='blue',marker='$'+nodes[i]+'$', markersize=15)
#突出显示最短路径节点名称
for i in range(len(path_xy)):
plt.plot(path_xy[i, 0], path_xy[i, 1], color='red',marker='$'+path[i]+'$', markersize=15)
#最短路径连线
getx = path_xy[:, 0]
gety = path_xy[:, 1]
plt.plot(getx, gety, color='grey', marker='.', markersize=3, linestyle='-.')
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.title("最短路径距离:"+str(adjMatrix[i1][i2]))
plt.show()
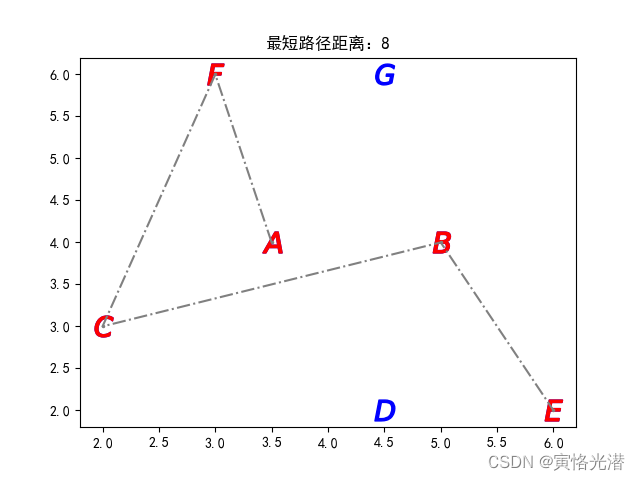
如果说两点之间的线上面再显示出权值(两点间距离),那就更完美了,有谁知道怎么做的,欢迎留言交流。


![[附源码]Python计算机毕业设计电视设备租借系统Django(程序+LW)](https://img-blog.csdnimg.cn/d83dde07ef94453aa6f862de8f278d62.png)


![[附源码]Python计算机毕业设计动物园动物饲养管理Django(程序+LW)](https://img-blog.csdnimg.cn/9cba6b752ecf456fb1af3b29731a712e.png)
![[附源码]Python计算机毕业设计电影推荐系统Django(程序+LW)](https://img-blog.csdnimg.cn/5461635ec900471cb7c8d1b67b3d4dd1.png)
![[附源码]Nodejs计算机毕业设计基于web的网上订餐系统Express(程序+LW)](https://img-blog.csdnimg.cn/61071535d27b4e31a3a549e51398226e.png)