文章目录：

二叉树链式结构实现
- 1.链式二叉树的结构
- 2.遍历二叉树
- - 2.1前序遍历
  - 2.2中序遍历
  - 2.3后序遍历
  - 2.4层序遍历
- 3.功能接口
- - 3.1二叉树节点个数
  - 3.2叶子节点个数
  - 3.3树的深度
  - 3.4第k层节点个数（k>=1）
  - 3.5查找目标节点
  - 3.6判断是否为完全二叉树
  - 3.7构建二叉树
  - 3.8销毁二叉树

二叉树链式结构实现

前面已经讲了二叉树的基础知识和堆的相关实现，不了解的友友们可以去看看我之前的文章树（C语言实现）和堆（C语言实现）（点击跳转），堆就是一颗用顺序结构实现的完全二叉树，下面我们来讲解一下链式结构实现的的二叉树，这部分接口主要是用递归实现的

递归三要素：

1. 函数功能
2. 限制条件
3. 等式

下面正文开始：

1.链式二叉树的结构

我们知道二叉树是由根节点、左子树、右子树三个部分组成的，细化到每个节点也是如此，所以可以将链式二叉树的每个节点都当作根节点，结构中存储的内容就可以分为：数据域，左子树和右子树三个部分

typedef int BTDataType; //数据类型

typedef struct BinaryTree
{
	BTDataType data; //数据域
	struct BinaryTree* left; //指向左子树（左孩子）
	struct BinaryTree* right; //指向右子树（右孩子）
}BTNode;

2.遍历二叉树

2.1前序遍历

先遍历根节点，再走到左子树，最后到右子树结束，遍历到根节点为NULL返回

//前序遍历
void PrevOrder(BTNode* root)
{
	//限制条件：根节点遍历到空了结束返回
	if (root == NULL)
	{
		printf("NULL");
		return;
	}
	printf("%d ", root->data); //先打印根节点信息（遍历根节点）
	PrevOrder(root->left); //再遍历左子树
	PrevOrder(root->right); //最后遍历走字数
}

2.2中序遍历

先遍历左子树，再走到根节点，最后到右子树结束，遍历到根节点为NULL返回

//中序遍历
void InOrder(BTNode* root)
{
	//限制条件：根节点遍历到空了结束返回
	if (root == NULL);
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left); //先遍历左子树
	printf("%d ", root->data); //再打印根节点信息（遍历根节点）
	InOrder(root->right); //最后遍历右子树
}

2.3后序遍历

先遍历左子树，再走到右子树，最后到根节点结束，遍历到根节点为NULL返回

//后序遍历
void PostOrder(BTNode* root)
{
	//限制条件：根节点遍历到空了结束返回
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left); //先遍历左子树
	PostOrder(root->right); //在遍历右子树
	printf("%d ", root->data); //最后打印根节点信息（遍历根节点）
}

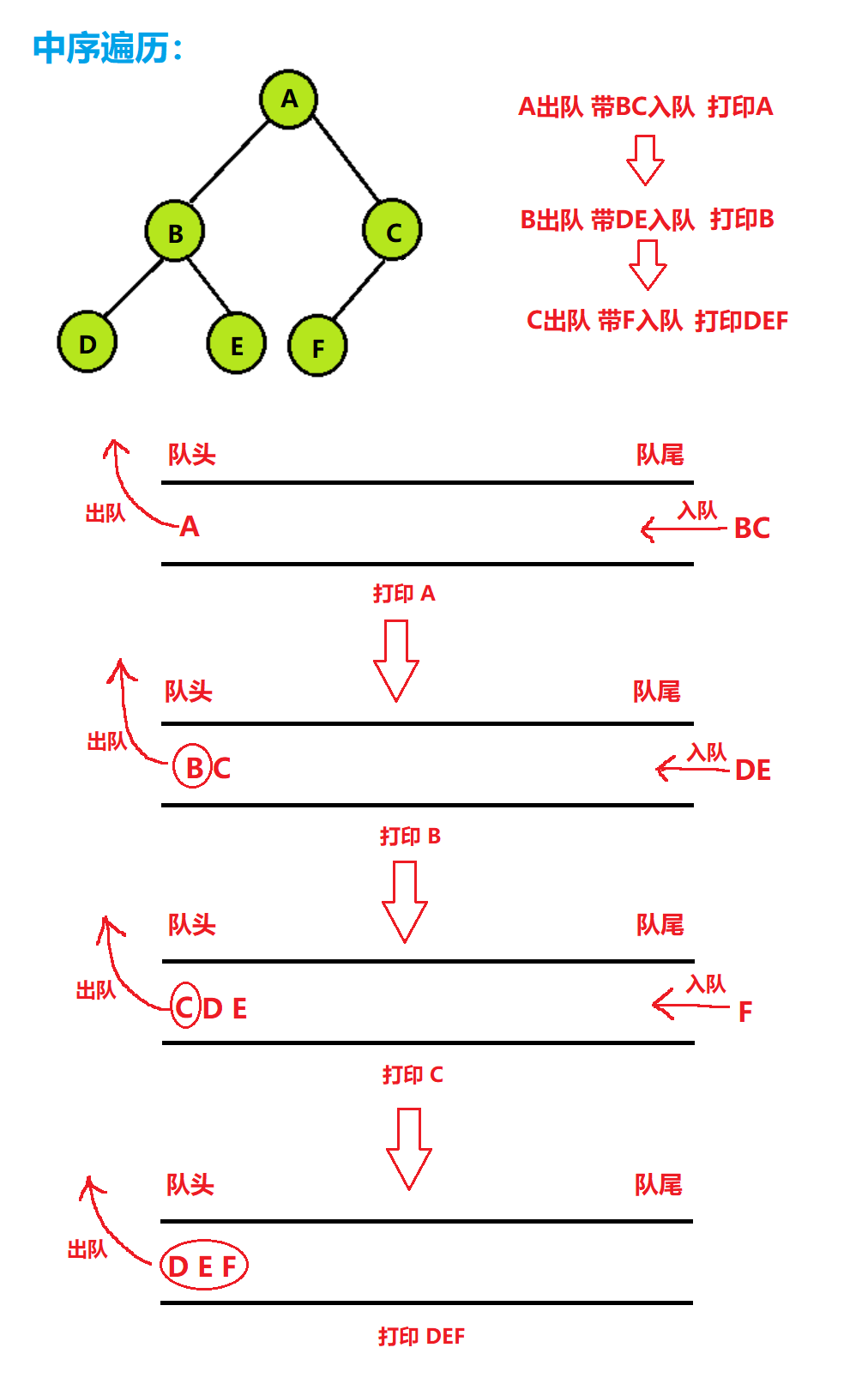
2.4层序遍历

二叉树的层序遍历是依靠队列来实现的，我们知道队列先进先出的特点，利用这一点我们来进行层序遍历，先让一层入队，然后出队打印，同时带着下一层入队，如此往复直到二叉树遍历完，当队列为空，就表示二叉树遍历完了，循环结束

//层序遍历
void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	int levelSize = 0;
	//根节点先入队
	if (root)
	{
		QueuePush(&q, root);
		levelSize = 1;
	}
	while (!QueueEmpty(&q))
	{
		//取头结点出队
		BTNode* front = QueueFront(&q);
		printf("%d ", front->data);
		QueuePop(&q);
		//带下一层入队
		if (root->left)
		{
			QueuePush(&q, front->left);
		}
		if (root->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
	QueueDestroy(&q);
}

图解：

3.功能接口

3.1二叉树节点个数

从根节点递归遍历左右子树求节点个数累积，根节点为NULL时结束返回0个节点

//二叉树节点个数
int TreeSize(BTNode* root)
{
	限制条件：根节点遍历到空了结束返回
	//等式：左子树节点个数 + 右子树节点个数 + 根节点
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

3.2叶子节点个数

从根节点递归遍历左右子树求叶子节点个数累加，根节点为空时结束返回0个节点，当节点的左右子树都为NULL时则为叶子节点，返回1个节点

//叶子节点个数
int TreeLeafSize(BTNode* root)
{
	//限制条件：根节点遍历到空了结束返回
	if (root == NULL)
	{
		return 0;
	}
	//限制条件：左右子树都为空则是叶子节点
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	//等式：左子树叶子节点个数 + 右子叶子树节点个数
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

3.3树的深度

从根节点开始遍历左右子树深度，返回更深的那个再加上第一层的根节点就是树的深度，当根节点为NULL时结束返回0，这里有个细节就是每次将遍历到的当前左右子树的深度记录下来再进行比较，少了这一步每次比较的时候会再次调用函数递归，导致运行速度大大降低

//树的深度
int TreeHeight(BTNode* root)
{
	//限制条件：根节点遍历到NULL时结束返回0个节点
	if (root == NULL)
	{
		return 0;
	}
	//记录
	int leftHeight = TreeHeight(root->left);
	int rightHeight = TreeHeight(root->right);
	//等式：返回更深的那颗子树加上第一层根节点就是树的深度
	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

3.4第k层节点个数（k>=1）

从根节点开始遍历左右子树每个节点返回1累加，因为第一层是根节点，这里的第k层就是左子树第k-1层节点数 + 右子树第k-1层节点数，节点为NULL时结束返回0个节点
…

//第k层节点个数（k>=1）
int TreeKLevelSize(BTNode* root, int k)
{
	//限制条件：根节点遍历到NULL时结束返回0个节点
	if (root == NULL)
	{
		return 0;
	}
	//限制条件：一个根节点返回1个节点
	if (k == 1)
	{
		return 1;
	}
	//等式：第k层节点树 = 左子树第k-1层节点数 + 右子树第k-1层节点数
	return TreeLeafSize(root->left, k - 1)
		+ TreeLeafSize(root->right, k - 1);
}

3.5查找目标节点

从根节点开始遍历左右子树查找目标节点，节点为空结束返回空，找到了结束返回目标节点，没找到返回空

//查找目标节点
BTNode* TreeFind(BTNode* root, BTDataType x)
{
	//限制条件：根节点遍历到时空结束返回空
	if (root == NULL)
		return NULL*
	//限制条件：找到目标节点结束返回目标节点
	if (root->data == x)
		return root;

	//递归遍历左右子树查找
	BTNode* ret1 = TreeFind(root->left, x);
	if (ret1)
		return ret1;
	BTNode* ret2 = TreeFind(root->right, x);
	if (ret2)
		return ret2;
	//找不到返回空
	return NULL;
}

3.6判断是否为完全二叉树

和层序遍历相似，核心思想也是：上一层出队，带着下一层入队，层序遍历中空节点是不入队的，这里我们全部入队，遇到空节点就开始进行判断，如果后面还有不为空的节点，则证明不连续就不是完全二叉树，反之则是

//判断是否为完全二叉树
bool TreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	//取每层
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//遇到空就开始判断
		if (!front) //遇到空，就开始判断
		{
			break;
		}
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}
	//出到空以后，如果后面全是空，则是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//不为NULL说明最后一层不是连续的,则不是完全二叉树
		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}

图解：

3.7构建二叉树

用一个数组中存放的二叉树前序遍历的结果来构建二叉树，# 代表NULL，这里我们直接遍历数组，遇到#就返回NULL，反之则申请一个节点作为根节点，利用前序遍历根->左->右的特点来链接还原这颗二叉树

通过前序遍历的数组'A,B,D,#,#,E,#,H,#,#,C,F,#,#,G,#,#'来还原二叉树

//构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
	//遇到#就返回空并向后遍历
	if (a[(*pi)] == '#')
	{
		(*pi)++;
		return NULL;
	}
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	if (root == NULL)
	{
		perror("BinaryTreeCreate: malloc is failed!\n");
		exit(-1);
	}
	//根节点
	root->data = a[(*pi)++];
	//左右子树
	root->left = BinaryTreeCreate(a, pi);
	root->right = BinaryTreeCreate(a, pi);

	return root;
}

3.8销毁二叉树

这里利用后序遍历来销毁二叉树，从后往前销毁不会影响到节点的指向，如果先销毁了根节点，那么下面的节点就丢失了这样是行不通的，这里最好传二级指针这样可以在销毁完后将根节点置空，防止野指针，传一级的话需要到主函数中手动置空不太方便

//销毁二叉树
void TreeDestroy(BTNode** root)
{
	//限制条件：根节点遍历到空结束返回
	if ((*root) == NULL)
	{
		return;
	}
	TreeDestroy(&((*root)->left));
	TreeDestroy(&((*root)->right));
	//释放置空根节点
	free((*root));
	*root == NULL;
}