A - To Be SaikyoA - To Be Saikyo
题目大意
有N个人,编号从1到N。每个人有一个整数分数,称为编程能力;第i个人的编程能力是Pi分。人1需要多少分才能成为最强者?换句话说,最小非负整数x是多少,使得对于所有i ≠ 1,满足P1 + x > Pi?
思路分析
为了使第1个人成为最强者,他需要比其他人的分数都高。找出所有其他人的分数中的最大值max。因此,答案是max + 1 - P1。如果max已经小于等于P1,则答案是0,因为第1个人已经是最强者。
时间复杂度
O(N)
AC代码
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> p(n);
for (int i = 0; i < n; i++) {
cin >> p[i];
}
int m = 0;
for (int i = 1; i < n; i++) {
m = max(m, p[i]); // 找到除了第一个人之外的最高分数
}
cout << max(0, m + 1 - p[0]) << endl;
return 0;
}
B - Who is Saikyo?B - Who is Saikyo?
题目大意
给定N个竞技选手,他们之间存在优劣关系。优劣关系具有传递性,即若选手A优于选手B,选手B优于选手C,则选手A优于选手C。定义最强选手为对其他所有选手具有优势的选手。给定M个关系信息,判断是否能确定最强选手,并输出其编号。如果有多个可能为最强选手,输出-1。
思路分析
右边为被超过,最强不可能出现右边,记录右边程序员出现的次数de[i]。
如果某个程序员的计数值de[i]为0,说明他没有被其他程序员所超过,他就可能是最强程序员。如果存在多个计数值为0的程序员(在它之前的ans!=-1),程序会输出-1并终止程序。否则,程序会将最强程序员的索引加1赋值给变量ans,并输出ans的值。
时间复杂度
O(N+M)
AC代码
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, m;
cin >> n >> m;
vector<int> deg(n);
while (m--) {
int a, b;
cin >> a >> b; /
--a, --b;
deg[b]++;
}
int ans = -1;
for (int i = 0; i < n; i++) {
if (deg[i] == 0) {
if (ans != -1) { // 如果已经有选手被赋值给ans
cout << -1 << endl; // 输出-1,表示无法确定最强选手
return 0;
} else {
ans = i + 1;
}
}
}
cout << ans << endl;
return 0;
}
C - Approximate Equalization 2C - Approximate Equalization 2
题目大意
给定一个整数序列A,可以进行以下操作任意次数(包括零次):
选择两个整数i和j(1≤i,j≤N),将A_i减一并将A_j加一。找到使得序列A的最大值和最小值之间的差最多为1所需的最小操作次数。
思路分析
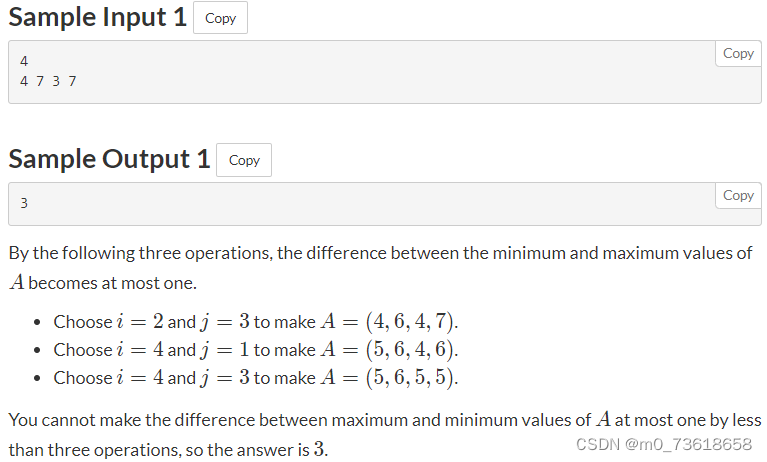
将最大值逐渐减小,将最小值逐渐增大,来使得最大值和最小值之间的差最多为1。
- 首先将序列A排序,这样最大值和最小值就会排列在序列a的末尾和开头。
- 然后构造一个均匀分布的序列b,使得序列b的平均值接近每个元素之和的平均值。
- 将多余的1分配给序列b的末尾的元素,以最大程度地减小操作次数。
- 最后,计算序列a和序列b的元素之间的差值,得到最小操作次数。
时间复杂度
O(NlogN)
AC代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int main() {
int n;
cin >> n;
vector<int> a(n);
ll sum = 0;
for (int i = 0; i < n; i++) {
cin >> a[i];
sum += a[i];
}
sort(a.begin(), a.end());
vector<int> b(n, sum / n); // 创建长度为N的数组b,初始值为sum/n
for (int i = 0; i < sum % n; i++) {
b[n - 1 - i]++; // 将sum % n个1分别分配给数组b的尾部元素
}
ll ans = 0;
for (int i = 0; i < n; i++) {
ans += abs(a[i] - b[i]);
}
cout << ans / 2 << endl;
}