这篇文章我们来介绍一下快速排序,主要分为:单边快排,双边快排,随机数基准点,算法优化四部分内容。
目录
1.快速排序的核心思想
2.具体实现方法
2.1单边循环(lomuto分区)
2.1.1单边循环(lomuto分区)要点
2.1.2代码实现
2.2双边快排
2.2.1双边快排的要点
2.2.2详细思路
2.2.3 代码实现
2.2.4 几个小问题
2.2.4使用随机元素作为基准点
2.3算法改进
2.3.1原因与分析
2.3.2代码实现
2.3.3 几个小问题
3.小结
1.快速排序的核心思想
首先,我们来说明一下快速排序的核心思想
核心思想:对一个无序的数组,我们先找一个基准点(随便找的,不同方法找的基准点是不一样的,后面会介绍不同的方法),然后想办法来循环比较,将比这个基准点小的数放到基准点的右边,比基准点大的数放到基准点的左边,这样我们就以基准点为界得到了两个分区,并且我们所确定的基准点,它在数组中的位置就确定了,然后我们再在这两个分区里面重复上述操作,直到元素比较完为止。
具体演示:
下面来看一下具体的图解

思考:
上面讲了快速排序的核心思想,下面我们来分析一下。首先,它用了分治思想,即分而治之的思想,将整体分成部分,然后再对部分进行处理。 其次,它用了递归思想,对整体处理,然后对部分处理,然后再对部分处理,那么递归结束的条件是什么呢?这个与不同方法的本身逻辑有关。下面介绍不同方法时再介绍。
我们再来思考它有哪些核心代码。首先肯定有一个递归函数,有哪些参数?肯定有数组,有数组的左右边界(也可以称为区的左右边界),它的作用就是调用我们的分区排序函数,进行递归;然后是分区比较函数,它的作用是实现分区,实现比较排序,然后返回基准点的索引;然后有数值交换函数,即交换数值,有哪些参数?肯定有数组,还有两个值的索引。有了这些基本逻辑,我们就可以来写快速排序的框架代码了。
快速排序的框架代码:
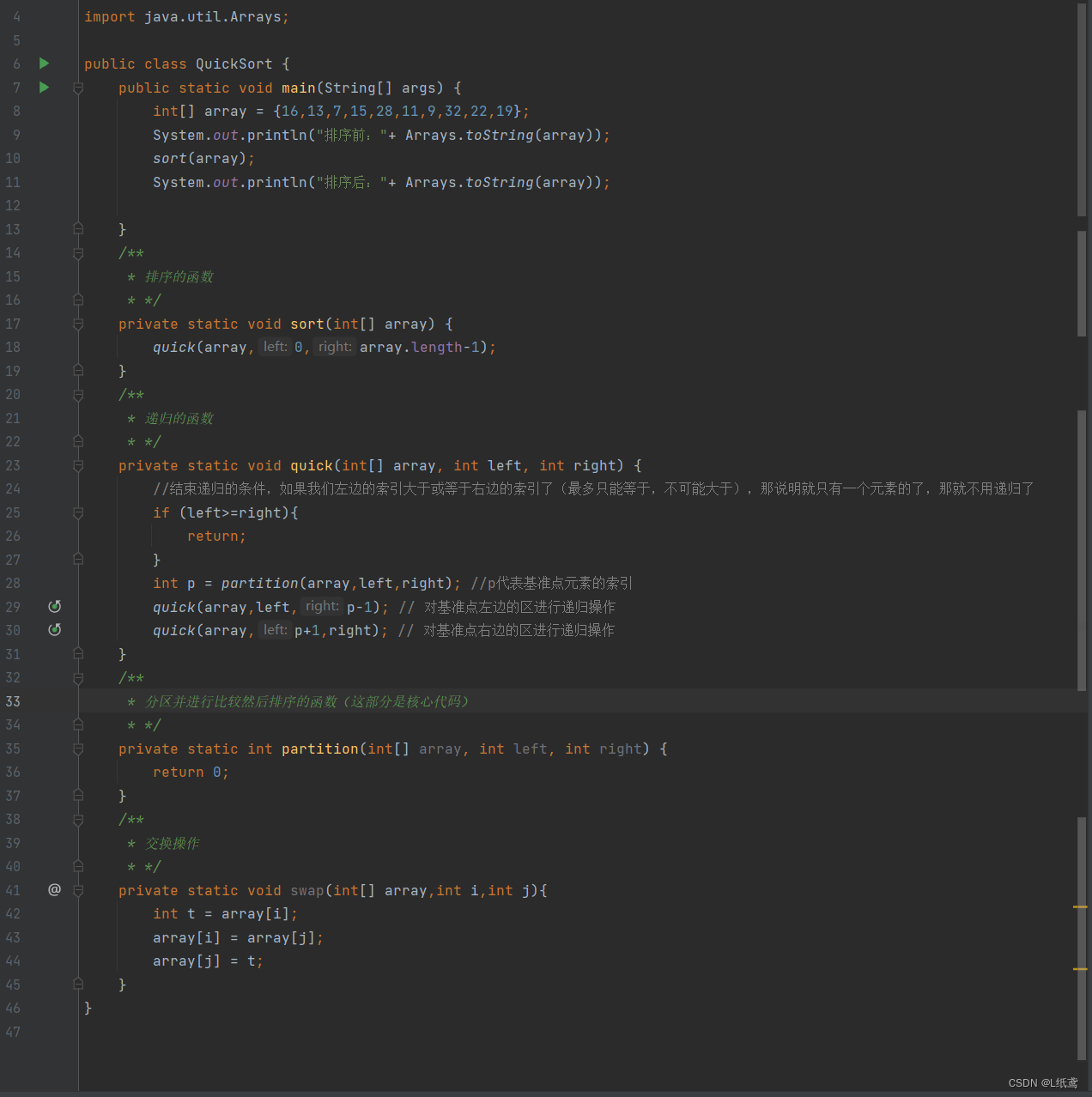
代码如下:
package Sorts;
import java.util.Arrays;
public class QuickSort {
public static void main(String[] args) {
int[] array = {16,13,7,15,28,11,9,32,22,19};
System.out.println("排序前:"+ Arrays.toString(array));
sort(array);
System.out.println("排序后:"+ Arrays.toString(array));
}
/**
* 排序的函数
* */
private static void sort(int[] array) {
quick(array,0,array.length-1);
}
/**
* 递归的函数
* */
private static void quick(int[] array, int left, int right) {
//结束递归的条件,如果我们左边的索引大于或等于右边的索引了(最多只能等于,不可能大于),那说明就只有一个元素的了,那就不用递归了
if (left>=right){
return;
}
int p = partition(array,left,right); //p代表基准点元素的索引
quick(array,left,p-1); // 对基准点左边的区进行递归操作
quick(array,p+1,right); // 对基准点右边的区进行递归操作
}
/**
* 分区并进行比较然后排序的函数(这部分是核心代码)
* */
private static int partition(int[] array, int left, int right) {
return 0;
}
/**
* 交换操作
* */
private static void swap(int[] array,int i,int j){
int t = array[i];
array[i] = array[j];
array[j] = t;
}
}
2.具体实现方法
下面来介绍一下具体的实现方法。上面说的只是快排的核心思想,但是具体实现还没说。因为快排的具体实现有许多种,这些方法的不同主要是因为我们选择的基准点不同,下面来详细说一下各种方法。
2.1单边循环(lomuto分区)
首先来介绍一下单边循环的方法,即lomuto分区的方法
2.1.1单边循环(lomuto分区)要点
要点:
- 选择区的最右边元素为基准点;
- 定义两个游标 i 与 j ,i 找比基准点大的元素,j 找比基准点小的元素,一旦找到,二者所指元素位置互换
- 最终,基准点与 i 交换,i 为基准点的最终索引
下面来看一下图解:
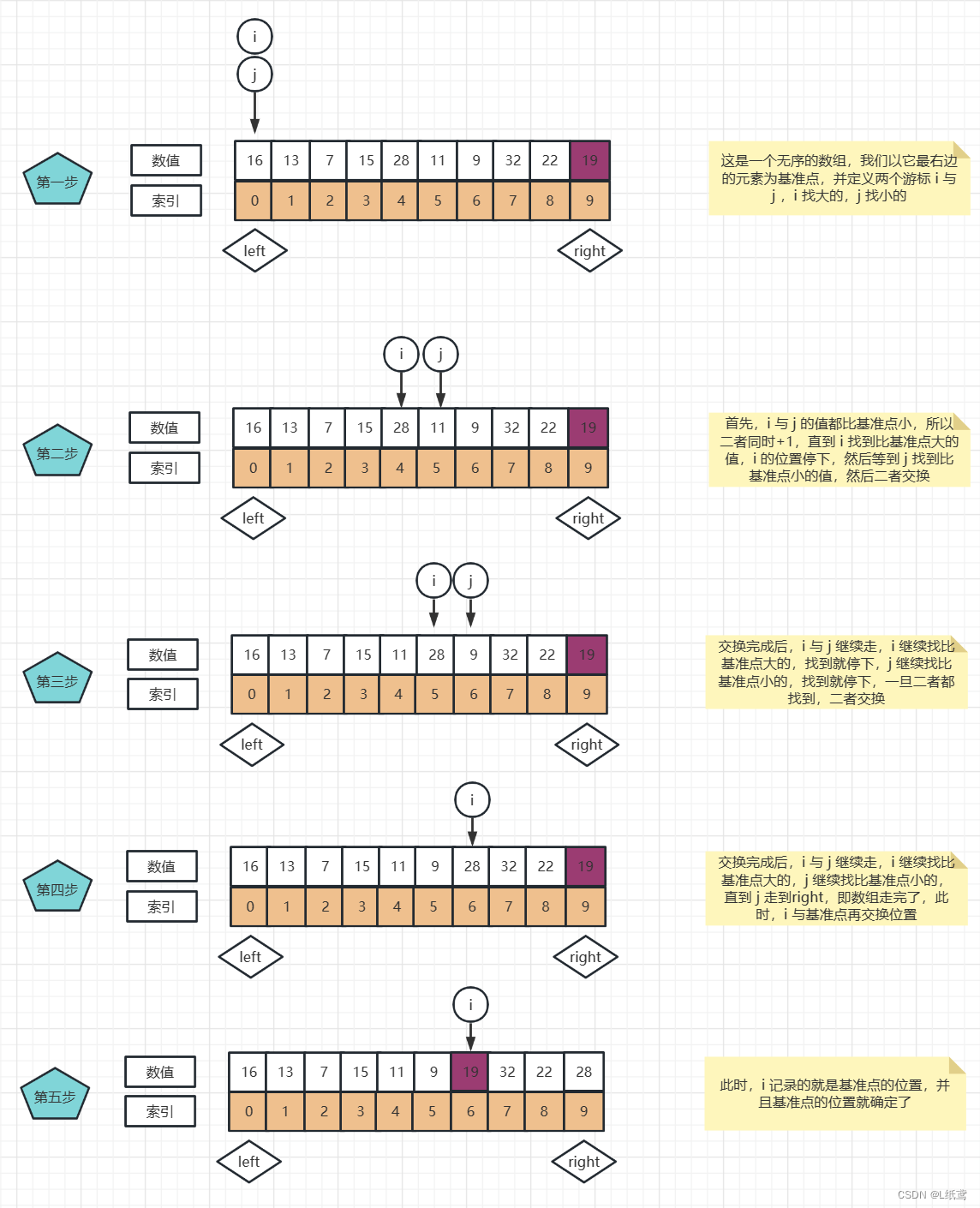
有一个小问题:i 与 j 在一开始的时候,j 已经比基准点小了,我们只需要走 i ,寻找比基准点大的值,然后交换就行了,为什么 j 也要走?
答:这里只能我也只能通过最终结果来说明一下(原理还是不清楚),如果按上述的走,那么 i 与 j 交换后,大的值就到前面去了,小的值就到后面来了,这与排序中要求的基准点左边值比基准点小,右边值比基准点大的准则相违背,所以 i 与 j 在一开始的时候都要走
2.1.2代码实现
下面来看一下实现的代码:
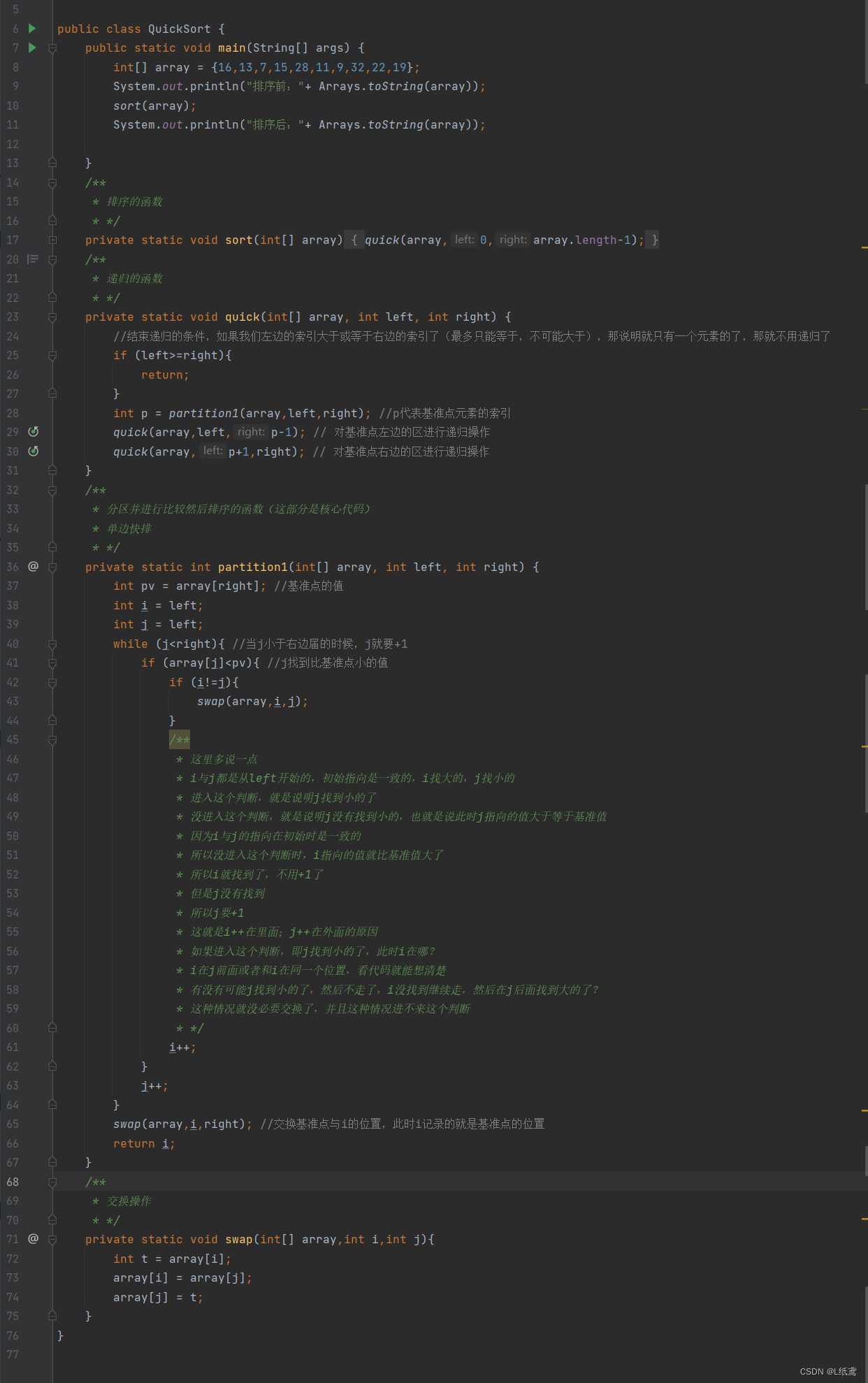
代码:
package Sorts;
import java.util.Arrays;
public class QuickSort {
public static void main(String[] args) {
int[] array = {16,13,7,15,28,11,9,32,22,19};
System.out.println("排序前:"+ Arrays.toString(array));
sort(array);
System.out.println("排序后:"+ Arrays.toString(array));
}
/**
* 排序的函数
* */
private static void sort(int[] array) {
quick(array,0,array.length-1);
}
/**
* 递归的函数
* */
private static void quick(int[] array, int left, int right) {
//结束递归的条件,如果我们左边的索引大于或等于右边的索引了(最多只能等于,不可能大于),那说明就只有一个元素的了,那就不用递归了
if (left>=right){
return;
}
int p = partition1(array,left,right); //p代表基准点元素的索引
quick(array,left,p-1); // 对基准点左边的区进行递归操作
quick(array,p+1,right); // 对基准点右边的区进行递归操作
}
/**
* 分区并进行比较然后排序的函数(这部分是核心代码)
* 单边快排
* */
private static int partition1(int[] array, int left, int right) {
int pv = array[right]; //基准点的值
int i = left;
int j = left;
while (j<right){ //当j小于右边届的时候,j就要+1
if (array[j]<pv){ //j找到比基准点小的值
if (i!=j){
swap(array,i,j);
}
/**
* 这里多说一点
* i与j都是从left开始的,初始指向是一致的,i找大的,j找小的
* 进入这个判断,就是说明j找到小的了
* 没进入这个判断,就是说明j没有找到小的,也就是说此时j指向的值大于等于基准值
* 因为i与j的指向在初始时是一致的
* 所以没进入这个判断时,i指向的值就比基准值大了
* 所以i就找到了,不用+1了
* 但是j没有找到
* 所以j要+1
* 这就是i++在里面;j++在外面的原因
* 如果进入这个判断,即j找到小的了,此时i在哪?
* i在j前面或者和i在同一个位置,看代码就能想清楚
* 有没有可能j找到小的了,然后不走了,i没找到继续走,然后在j后面找到大的了?
* 这种情况就没必要交换了,并且这种情况进不来这个判断
* */
i++;
}
j++;
}
swap(array,i,right); //交换基准点与i的位置,此时i记录的就是基准点的位置
return i;
}
/**
* 交换操作
* */
private static void swap(int[] array,int i,int j){
int t = array[i];
array[i] = array[j];
array[j] = t;
}
}
一个小问题:代码的第40行,我们为什么不能用 i 来进行循环,即写成 i < right?
答:可以的,只不过这样排出来是倒序的。
下面根据代码来讲述一下单边快排的原理。首先找基准点,然后定义游标 i 与 j,它们都是从left位置开始检索的,i 找大的,j 找小的。我们最终要的是以基准点为界,左边是比基准点小的,右边是比基准点大的,所以如果 i 与 j 都指向小的,那么该元素的位置是对的,不用交换, i 与 j 都往后走,这就是为什么 j 要在外面+1了,如果找到了一个大的,那么 i 的位置停下,j 继续走,知道 j 再找到小的,然后进行交换。其实这里饶了一个小弯,我们的思维是这样想的,但是代码实现的条件判断确实 j 的值是否比基准点小。其实这里还不够细致。 i 与 j 移动后,要用值与基准点进行比较,比较结束后,再决定进行何种操作。
真正的思路是这样的: i 与 j 一开始从left开始,即二者都指向left,然后进行判断,我们就用 j 指向的值来判断,如果小,那就交换,然后 i++,j++;如果大,此时 i 的位置找到了,那么就只需要j++了。问:能不能用 i 的值来进行判断?能,但是这样排出来后是倒序的。
2.2双边快排
下面来介绍一下双边快排。
2.2.1双边快排的要点
要点:
- 选择最左边的元素作为基准点;
- 定义两个游标 i 与 j;i 从最左边开始往右进行检索,找比基准点大的;j 从最右边往左进行检索,找比基准点小的,二者同时找到后,交互元素的位置
- 最后,基准点与 i 所指元素进行交换,最终 i 记录的就是基准点的位置
2.2.2详细思路
思路:
首先,我们会有一个无序数组,然后,我们将其最左边的元素设为基准点。然后,我们定义两个游标 i 与 j,i 在最左边,从左向右走,找比基准点大的数,j 在最右边,从右向左走,找比基准点小的数。现在 i 开始走,i++,进行判断,不比基准点大(即小于等于基准点),再 i++,再判断,比基准点大了,i 不走了,然后看 j (j也在走),j 比基准点大,j--,然后再比较,j 比基准点小了,然后 j 不走了,然后交换 i 与 j 所指的值,然后重复上述步骤,一直到什么时候呢?一直到 i = j 的时候,即二者重合的时候,此时数组就遍历完了。然后,再将 i 所指的值与基准值交换,这样基准值的位置就确定了。
仔细想一下,上面这一趟走完,基准值左边的数都比基准值小,右边的都比基准值大。
2.2.3 代码实现
下面看一下代码实现:
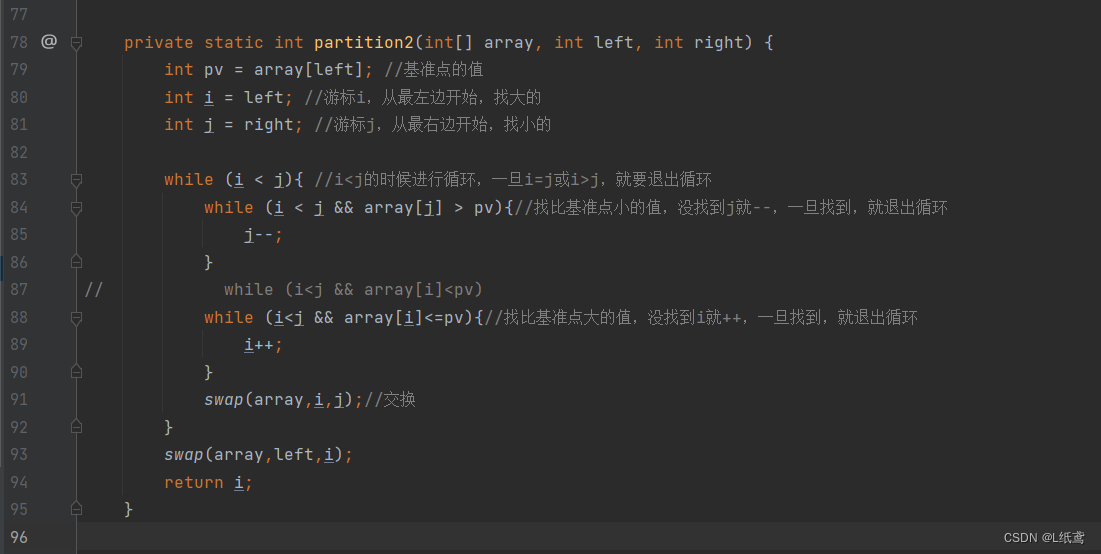
具体代码:
private static int partition2(int[] array, int left, int right) {
int pv = array[left]; //基准点的值
int i = left; //游标i,从最左边开始,找大的
int j = right; //游标j,从最右边开始,找小的
while (i < j){ //i<j的时候进行循环,一旦i=j或i>j,就要退出循环
while (i < j && array[j] > pv){//找比基准点小的值,没找到j就--,一旦找到,就退出循环
j--;
}
// while (i<j && array[i]<pv)
while (i<j && array[i]<=pv){//找比基准点大的值,没找到i就++,一旦找到,就退出循环
i++;
}
swap(array,i,j);//交换
}
swap(array,left,i);
return i;
}其余的代码都是与上面一样的,这里只展示了不一样的部分
2.2.4 几个小问题
问题一:第84行和第88行的内层循环条件中,为什么要加上 i<j 这个条件?
答:假设不加,则会出现这样一种情况,j 找小的,找啊找,找到一个,j 停下,然后 i 找大的,找啊找,找到一个,但是这个大的在小的后面,这时如果再交换就是一种错误的逻辑了。所以我们要加上
问题二:内存的两个循环的位置能不能互换?即先循环 i ,再循环 j?
答:不行。 仔细思考可以发现,先循环 j ,再循环 i,最后游标停在 j 处(即游标停止的原因是因为i++,i 要 >=j 了),即停在一个比基准点小的值的地方。如果先循环 i ,再循环 j,最后基准点会停在 i 处,即一个比基准点大的地方。所以应该先先循环 j,再循环 i 。
问题三:上图的第87行,循环条件写的是array[i] < pv,最后运行结果出错,而写成array[i] <= pv却是正确的,为什么?
答:因为 i 一开始是从最左边开始的,基准点也在最左边,也就是说,一开始的时候,i 就指向基准点。如果不加=,就表示只有在 i 小于基准点的时候才能进入循环,因为 i 的初始值与基准点相同,所以 i 就不可能进入循环,所以结果出错。
2.2.4使用随机元素作为基准点
前面讲了使用最右边和最左边元素作为基准点的两种方法,下面来讲一下如何使用随机元素作为基准点。
问题:为什么要使用随意元素作为基准点?
答: 为了预防极端情况的出现。比如一个倒序的数组,现在用双边快排来进行排序,第一轮分区排序后,左边有n-1个数据,右边只有一个数据,会极端的不平衡,这就导致递归的时候,一边要处理n-1个数据,一边不用处理数据,时间复杂度会增大,这种情况下的时间复杂度为n^2.
为了解决这个问题,所以我们需要使用随机元素来作为基准点
代码实现:

private static int partition3(int[] array, int left, int right) {
int idx = ThreadLocalRandom.current().nextInt(right-left+1)+left;//生成范围内的随机数
swap(array,idx,left);//交换随机数与left的值
int pv = array[left];//基准点的值
int i = left; //游标i,从最左边开始,找大的
int j = right; //游标j,从最右边开始,找小的
while (i < j){ //i<j的时候进行循环,一旦i=j或i>j,就要退出循环
while (i < j && array[j] > pv){//找比基准点小的值,没找到j就--,一旦找到,就退出循环
j--;
}
// while (i<j && array[i]<pv)
while (i<j && array[i]<=pv){//找比基准点大的值,没找到i就++,一旦找到,就退出循环
i++;
}
swap(array,i,j);//交换
}
swap(array,left,i);
return i;
}这个没啥好说的,根据分区内的元素个数,生成在left到分区终点范围内的一个随机数,然后交换随机数(即基准点的位置)与left的值,这样就确定了随机确定了一个基准点了。
其实,这个基准点还是在最左边,只不过基准点的值是随机的,这样就避免了极端情况的出现。
2.3算法改进
下面对这个算法进行以下改进
2.3.1原因与分析
问题:考虑这样一种极端情况,如果数组中的数都相等,在运用双边快排的时候会发生什么?
答:会出现分区极端不平衡的情况。j 在遇到小于等于基准点的值时会停下,所以 j 一开始就停下了,i 要一直检索到最后一个元素,然后 i 与基准点交换,这样基准点的左边就有n-1个元素,右边没有元素,分区极端不平衡。并且对于这种重复元素,前面的随机基准点也没用。、
那怎么解决呢?
上述问题的原因是:j 遇到等于基准点的值会停下,如果 j 和 i 一样,只有遇到小的值的时候再停下是否可以?不可以,这样会导致在基准点右半区有和基准点一样的值,不符合排序规则。那应该怎么做?换个角度想,因为 i 遇到相等的值不停,所以它会一直跑,跑到最后面,如果 i 遇到等于的值或大于的值的时候就停下来,然后 j 遇到小于或等于的值就停下来然后交换,这样就可以了。那么 i 的起始位置要变,不能为left了,要改为left+1了。交换完成后,i++,j--,这个时候可能 i > j;比如,i 与 j 相遇,然后满足条件,交换,然后i++,j--,然后就i > j,所以最后与基准点交换的应该是 j ,因为 j 指向的值永远比基准点小。
OK,上面就是具体思路了,下面来代码实现
2.3.2代码实现
下面看一下具体的代码实现:

private static int partition4(int[] array, int left, int right) {
int pv = array[left];//基准点的值
int i = left+1; //游标i,从left+1开始,找大的
int j = right; //游标j,从最右边开始,找小的
while (i <= j){ //i<=j的时候进行循环,一旦i>j,就要退出循环,当i=j的时候也要进入循环
while (i <= j && array[j] > pv){//找比基准点小或等于的值,没找到j就--,一旦找到,就退出循环
j--;
}
while (i<=j && array[i] < pv){//找比基准点大或相等的值,没找到i就++,一旦找到,就退出循环
i++;
}
if (i<=j){
swap(array,i,j);//交换
i++;
j--;
}
}
swap(array,left,j);
return j;
}2.3.3 几个小问题
问题:第124行,能不能把 i <=j 改为 i <j ?为什么?
答:不行,如果改为 i < j ,当 i 与 j 相遇如果停下后,不会进入循环,此时交换 j 与基准点就会导致 i 所指的值比基准点大,就导致基准点前面有比基准点大的值,就无法满足排序的规则了
3.小结
这篇文章主要讲了快速排序。再次说一下它的核心思想:找一个基准点,然后定义两个游标,一个找小的,一个找大的,同时找到了就交换,最后再与基准点交换位置,这样基准点的左边都是比它小的,右边都是比它大的。我们也称这轮操作为分区。
根据不同的分区方法,我们讲述了单边快排,以最右边元素为基准点;双边快排,以最左边元素为基准点;为了解决极端情况,我们引入了随机数基准点;为了处理重复的元素,我们对算法做了优化,改变了初始游标的位置和游标停止条件,以及交换的元素位置,形成了最终优化后的快速排序代码。
最后说一下感悟:慢下来,仔细逐帧思考剖析每一步操作,找出这些操作中各个变量间的关系,首先在具体问题中找变量与变量间的内在联系,找不到了再跳出题目,从整个题目出发思考一个条件的设置。最后就是要多画图,画图比只思考要直观的多。
最后,附赠全部代码:
package Sorts;
import java.util.Arrays;
import java.util.concurrent.ThreadLocalRandom;
public class QuickSort {
public static void main(String[] args) {
int[] array = {16,13,7,15,28,11,9,32,22,19};
int[] array1 = {4,2,1,3,2,4};
System.out.println("排序前:"+ Arrays.toString(array1));
sort(array1);
System.out.println("排序后:"+ Arrays.toString(array1));
}
/**
* 交换操作
* */
private static void swap(int[] array,int i,int j){
int t = array[i];
array[i] = array[j];
array[j] = t;
}
/**
* 排序的函数
* */
private static void sort(int[] array) {
quick(array,0,array.length-1);
}
/**
* 递归的函数
* */
private static void quick(int[] array, int left, int right) {
//结束递归的条件,如果我们左边的索引大于或等于右边的索引了(最多只能等于,不可能大于),那说明就只有一个元素的了,那就不用递归了
if (left>=right){
return;
}
int p = partition4(array,left,right); //p代表基准点元素的索引
quick(array,left,p-1); // 对基准点左边的区进行递归操作
quick(array,p+1,right); // 对基准点右边的区进行递归操作
}
/**
* 分区并进行比较然后排序的函数(这部分是核心代码)
* 单边快排
* */
private static int partition1(int[] array, int left, int right) {
int pv = array[right]; //基准点的值
int i = left;
int j = left;
while (j<right){ //当j小于右边届的时候,j就要+1
if (array[j]<pv){ //j找到比基准点小的值
if (i!=j){
swap(array,i,j);
}
/**
* 这里多说一点
* i与j都是从left开始的,初始指向是一致的,i找大的,j找小的
* 进入这个判断,就是说明j找到小的了
* 没进入这个判断,就是说明j没有找到小的,也就是说此时j指向的值大于等于基准值
* 因为i与j的指向在初始时是一致的
* 所以没进入这个判断时,i指向的值就比基准值大了
* 所以i就找到了,不用+1了
* 但是j没有找到
* 所以j要+1
* 这就是i++在里面;j++在外面的原因
* 如果进入这个判断,即j找到小的了,此时i在哪?
* i在j前面或者和i在同一个位置,看代码就能想清楚
* 有没有可能j找到小的了,然后不走了,i没找到继续走,然后在j后面找到大的了?
* 这种情况就没必要交换了,并且这种情况进不来这个判断
* */
i++;
}
j++;
}
swap(array,i,right); //交换基准点与i的位置,此时i记录的就是基准点的位置
return i;
}
/**
* 双边快排
* */
private static int partition2(int[] array, int left, int right) {
int pv = array[left]; //基准点的值
int i = left; //游标i,从最左边开始,找大的
int j = right; //游标j,从最右边开始,找小的
while (i < j){ //i<j的时候进行循环,一旦i=j或i>j,就要退出循环
while (i < j && array[j] > pv){//找比基准点小的值,没找到j就--,一旦找到,就退出循环
j--;
}
// while (i<j && array[i]<pv)
while (i<j && array[i]<=pv){//找比基准点大的值,没找到i就++,一旦找到,就退出循环
i++;
}
swap(array,i,j);//交换
}
swap(array,left,i);
return i;
}
/**
* 定义随机的基准点
* */
private static int partition3(int[] array, int left, int right) {
int idx = ThreadLocalRandom.current().nextInt(right-left+1)+left;//生成范围内的随机数
swap(array,idx,left);//交换随机数与left的值
int pv = array[left];//基准点的值
int i = left; //游标i,从最左边开始,找大的
int j = right; //游标j,从最右边开始,找小的
while (i < j){ //i<j的时候进行循环,一旦i=j或i>j,就要退出循环
while (i < j && array[j] > pv){//找比基准点小的值,没找到j就--,一旦找到,就退出循环
j--;
}
while (i<j && array[i]<=pv){//找比基准点大的值,没找到i就++,一旦找到,就退出循环
i++;
}
swap(array,i,j);//交换
}
swap(array,left,i);
return i;
}
/**
* 改进后的算法
* 为了处理重复的元素
* */
private static int partition4(int[] array, int left, int right) {
int pv = array[left];//基准点的值
int i = left+1; //游标i,从left+1开始,找大的
int j = right; //游标j,从最右边开始,找小的
while (i <= j){ //i<=j的时候进行循环,一旦i>j,就要退出循环,当i=j的时候也要进入循环
while (i <= j && array[j] > pv){//找比基准点小或等于的值,没找到j就--,一旦找到,就退出循环
j--;
}
while (i<=j && array[i] < pv){//找比基准点大或相等的值,没找到i就++,一旦找到,就退出循环
i++;
}
if (i<=j){
swap(array,i,j);//交换
i++;
j--;
}
}
swap(array,left,j);
return j;
}
}