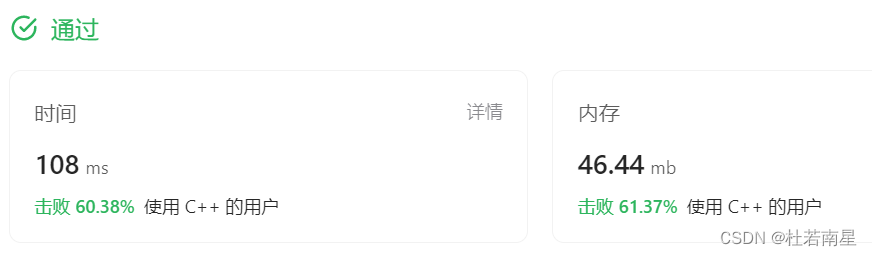
题目来源：https://leetcode.cn/problems/target-sum/description/

 

 C++题解（来源代码随想录）：将该问题转为01背包问题。

假设加法的总和为x，那么减法对应的总和就是sum - x。所以我们要求的是 x - (sum - x) = target。x = (target + sum) / 2。此时问题就转化为，装满容量为x的背包，有几种方法。

1. 确定dp数组以及下标的含义。（1）dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法。（2）也可以使用二维dp数组来求解本题，dp[i][j]：使用 下标为[0, i]的nums[i]能够凑满j（包括j）这么大容量的包，有dp[i][j]种方法。
2. 确定递推公式。只要搞到nums[i]，凑成dp[j]就有dp[j - nums[i]] 种方法。
3. dp数组如何初始化。dp[0] = 1。
4. 确定遍历顺序。对于01背包问题一维dp的遍历，nums放在外循环，target在内循环，且内循环倒序。

// 代码随想录版本
class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int S) {
        int sum = 0;
        for (int i = 0; i < nums.size(); i++) sum += nums[i];
        if (abs(S) > sum) return 0; // 此时没有方案
        if ((S + sum) % 2 == 1) return 0; // 此时没有方案
        int bagSize = (S + sum) / 2;
        vector<int> dp(bagSize + 1, 0);
        dp[0] = 1;
        for (int i = 0; i < nums.size(); i++) {
            for (int j = bagSize; j >= nums[i]; j--) {
                dp[j] += dp[j - nums[i]];
            }
        }
        return dp[bagSize];
    }
};

// 一维数组版本
class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        // left + right = sum;
        // left - right = target;
        // left = (sum + target) / 2;
        // 01背包：背包总量left，价值和为j的个数为dp[j]
        // dp[j] = dp[j]+dp[j-nums[i]]

        int len = nums.size();
        int sum = 0;
        for(int i = 0; i < len; i++) {
            sum = sum + nums[i];
        }
        if(sum < target || target < -sum) return 0;
        else if((sum - target) % 2 == 1) return 0;
        int left = (sum + target) / 2;
        vector<int> dp(left+1, 0);
        dp[0] = 1;       // 初始化
        if(nums[0] <= left) dp[nums[0]]++;  // 考虑left = nums[0] = 0的情况
        for(int i = 1; i < len; i++) {
            for(int j = left; j >= nums[i]; j--) {
                dp[j] = dp[j] + dp[j-nums[i]];
            }
        }
        return dp[left];
    }
};

// 二维数组版本
class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        // left + right = sum;
        // left - right = target;
        // left = (sum + target) / 2;
        // 01背包：背包总量left，在0-i个物品中，价值和为j的个数为dp[i][j]
        // dp[i][j] = dp[i-1][j]+dp[i-1][j-nums[i]]

        int len = nums.size();
        int sum = 0;
        for(int i = 0; i < len; i++) {
            sum = sum + nums[i];
        }
        if(sum < target || target < -sum) return 0;
        else if((sum - target) % 2 == 1) return 0;
        int left = (sum + target) / 2;
        vector<vector<int>> dp(len, vector<int>(left+1, 0));
        dp[0][0] = 1;       // 初始化
        if(nums[0] <= left) dp[0][nums[0]]++;  // 考虑left = nums[0] = 0的情况
        for(int i = 1; i < len; i++) {
            for(int j = 0; j <= left; j++) {
                if(j < nums[i]) dp[i][j] = dp[i-1][j];
                else dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]];
            }
        }
        return dp[len-1][left];
    }
};