今日份题目:
请定义一个队列并实现函数 max_value 得到队列里的最大值,要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。
若队列为空,pop_front 和 max_value 需要返回 -1
示例1
输入:
["MaxQueue","push_back","push_back","max_value","pop_front","max_value"]
[[],[1],[2],[],[],[]]
输出: [null,null,null,2,1,2]示例2
输入:
["MaxQueue","pop_front","max_value"]
[[],[],[]]
输出: [null,-1,-1]提示
-
1 <= push_back,pop_front,max_value的总操作数 <= 10000 -
1 <= value <= 10^5
题目思路及代码
方法一:暴力算法
class MaxQueue
{
public:
queue<int> p,temp;
MaxQueue() { }
int max_value() //遍历queue中所有的元素得到最大值
{
if(p.empty()) return -1;
int maxm=INT_MIN;
while(!p.empty())
{
int cur=p.front();
p.pop();
temp.push(cur);
maxm=max(maxm,cur);
}
while(!temp.empty())
{
int cur=temp.front();
temp.pop();
p.push(cur);
}
return maxm;
}
void push_back(int value)
{
p.push(value);
}
int pop_front()
{
if(p.empty()) return -1;
int cur=p.front();
p.pop();
return cur;
}
};
/**
* Your MaxQueue object will be instantiated and called as such:
* MaxQueue* obj = new MaxQueue();
* int param_1 = obj->max_value();
* obj->push_back(value);
* int param_3 = obj->pop_front();
*/方法二:维护一个单调递减的双端队列
使用单调递减的双端队列记录到目前为止的最大值和后续比这个值小的依次最大值,以便在最大值删除后能够找到后续的最大值。
class MaxQueue
{
queue<int> p;//存放内容的正常操作队列
deque<int> d;//单调递减的双端队列,存放当前为止的最大值及后续小值,以便前边的大值删掉后不影响后续队列中元素的最大值的记录
public:
MaxQueue() { }
int max_value()
{
if(p.empty()) return -1;//队列为空
return d.front();//因为是单减的双端队列,所以front就是最大值
}
void push_back(int value)
{
while(!d.empty()&&d.back()<value) //维护一个单调递减的双端队列
{
d.pop_back();
}
d.push_back(value);
p.push(value);
}
int pop_front()
{
if(p.empty()) return -1;//队列为空
int ans=p.front();
p.pop();
if(ans==d.front()) //最大值是当前要删除的元素,那么双端队列中也要删
{
d.pop_front();
}
return ans;
}
};
/**
* Your MaxQueue object will be instantiated and called as such:
* MaxQueue* obj = new MaxQueue();
* int param_1 = obj->max_value();
* obj->push_back(value);
* int param_3 = obj->pop_front();
*/提交结果
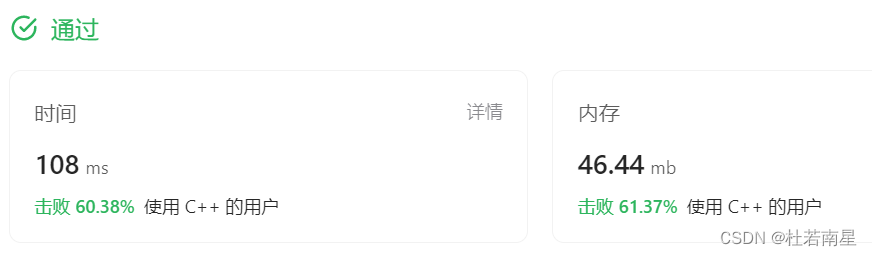
暴力算法
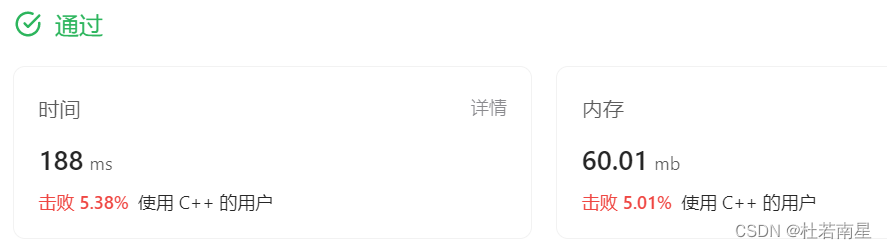
维护一个单调递减的双端队列