题目描述

题目链接：剑指 Offer II 113. 课程顺序 - 力扣（Leetcode）

现在总共有 numCourses 门课需要选，记为 0 到 numCourses-1。

给定一个数组 prerequisites ，它的每一个元素 prerequisites[i] 表示两门课程之间的先修顺序。例如 prerequisites[i] = [ai, bi] 表示想要学习课程 ai ，需要先完成课程 bi 。

请根据给出的总课程数 numCourses 和表示先修顺序的 prerequisites 得出一个可行的修课序列。

可能会有多个正确的顺序，只要任意返回一种就可以了。如果不可能完成所有课程，返回一个空数组。

示例 1：

输入: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出: [0,1,2,3] or [0,2,1,3]
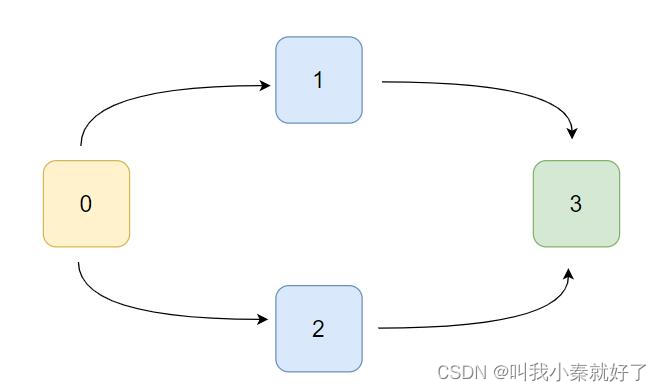
解释: 总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。

请添加图片描述

示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：[]

提示：

1 <= numCourses <= 105
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
prerequisites[i] 中的所有课程对 互不相同

拓扑排序

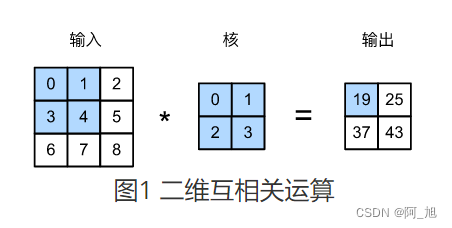
我们会把生产流程、软件开发、课程安排等都当成一个项目工程来对待，所有的工程都可分为若干个 “活动“ 的子工程。在这些活动之间，通常会受到一定的条件约束，如其中某些活动必须在另一些活动完成之后才能开始。就像上图 1 课程要在 0 课程之后学，3 课程要在 1 课程之后学。因此这样的工程图，一定是无环的有向图。

设 G=(V,E) 是一个具有 n 个顶点的有向图，V 中的顶点序列 $v_1, v_2, ... v_n$ ，若满足有从顶点 $v_i$ 到 $v_j$ 的路径，则顶点序列中 $v_i$ 在 $v_j$ 之前。那么称这样的顶点序列为一个拓扑序列。

所谓拓扑排序，就是对一个有向图构造拓扑序列的过程。

同时，也需要了解入度和出度的概念：

入度：以该顶点为终点的有向边数量，即有多少条边直接指向该顶点
出度：以该顶点为起点的有向边数量，即由该顶点指出的边有多少

因此，对于有向图的拓扑排序，可以使用如下思路输出拓扑序列（BFS）：

开始时，将所有入度为 0 的顶点加入队列
- 入度为 0，说明没有边指向该顶点，放到拓扑序列的首部，不会违反定义
在队列中进行出队操作，出队顺序就是我们要找的拓扑序列。对于当前弹出的顶点 x，遍历 x 的所有出度，即所有由 x 指向的顶点 y，对 y 做入度减 1 操作
- 因为 y 需要的一个前提已经准备就绪了，就可以其减去
对 y 进行减 1 操作后，检查 y 的入度是否为 0，如果为 0 则将 y 入队
- 如果 y 所有前提都准备好了，就可以执行 y 操作了
循环流程 2、3 直到队列为空

建图 + 拓扑排序

回到本题，我们可以根据题目给出的 prerequisites 建图。若课程 a 存在前置课程 b 的话，就添加一条从 b 到 a 的有向边，同时统计所有课程的入度。

当建完图后，将所有入度为 0 的课程进行入队操作，进行拓扑排序，若得到的序列的课程数等于给出的课程数，说明有合理的顺序，否则返回空。

代码：

class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> edges(numCourses);
        // 用来记录每个顶点的入度
        vector<int> inDeg(numCourses);              
        // 建图并记录入度
        for (const auto& pre : prerequisites) {
            edges[pre[1]].push_back(pre[0]);
            inDeg[pre[0]]++;
        }
        
        queue<int> q;
        // 将度为 0 入队
        for (int i = 0; i < numCourses; i++) {
            if (inDeg[i] == 0) {
                q.push(i);
            }
        }

        vector<int> ans;
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            ans.push_back(u);
            for (int v : edges[u]) {
                inDeg[v]--;
                if (inDeg[v] == 0) {
                    // 此时说明前置课程都学习过了
                    q.push(v);
                }
            }
        }
        return (ans.size() == numCourses) ? ans : vector<int>();
    }
};