MATLAB 使用算法来生成伪随机数和伪独立数。这些数在数学意义上并非严格随机和独立的,但它们能够通过各种随机和独立统计测试,并且其计算可以重复,方便用于测试或诊断目的。
rand
、
randi
、
randn
和
randperm
函数是创建随机数数组的主要函数。
rng 函数允许您控制生成随机数的种子和算法。
1.随机数函数
有四种基本随机数函数:rand
、
randi
、
randn
和
randperm
。
rand 函数返回在 0 和 1 之间均匀分布的浮点数。例如:
rng('default')
r1 = rand(1000,1);
r1 是一个含有均匀分布浮点实数的 1000 x 1 的列向量。
r1 中的所有值均处于开区间 (0, 1) 内。这些值的直方图大致上是扁平形状,这表明采样数相当均匀。
randi 函数返回离散均匀分布中的
double
整数值。例如,
r2 = randi(10,1000,1);
r2 是一个包含范围在闭区间 [1, 10] 的离散均匀分布整数值的 1000×1 列向量。这些值的直方图大致上是扁平形状,这表明从 1 到 10 之间采样数相当均匀。
randn 函数返回标准正态分布中的浮点实数数组。例如:
r3 = randn(1000,1);
r3 是一个含有标准正态分布数的 1000 x1 的列向量。
r3 的直方图看似大致上均值为 0 且标准差为 1 的正态分布。
可以使用 randperm
函数创建一个由没有重复值的随机整数值组成的
double
数组。例如,
r4 = randperm(15,5);
r4 是 1×5 数组,包含从范围 [1, 15] 中随机选择的整数。与可返回包含重复值的数组的
randi 不同,randperm 返回的数组没有重复值。接连调用上述任一函数均可返回不同的结果。这种特性适合用于创建几个不同的随机值数组。
2.随机数生成器
MATLAB 提供几个生成器算法选项,下表对其进行了总结。

使用 rng
函数可设置
rand
、
randi
、
randn
和
randperm
函数使用的种子和生成器。例如,
rng(0,'twister') 将生成器重置为其默认状态。
3.随机数的数据类型
rand 和
randn
函数默认情况下会生成双精度类型的值。
rng('default')
A = rand(1,5);
class(A)
ans = 'double'
要将类显式指定为双精度类型:
rng('default')
B = rand(1,5,'double');
class(B)
ans = 'double'
isequal(A,B)
ans =
1
rand 和
randn
也可以生成单精度类型的值。
rng('default')
A = rand(1,5,'single');
class(A)
ans = 'single'
这些值与转换前一示例中的双精度值相同。无论返回哪种类的值,这些函数获取的随机流都会以相同方式增加。
A,B
A =
0.8147 0.9058 0.1270 0.9134 0.6324
B =
0.8147 0.9058 0.1270 0.9134 0.6324
randi 既支持整数类型,又支持单精度或双精度类型。
A = randi([1 10],1,5,'double');
class(A)
ans = 'double'
B = randi([1 10],1,5,'uint8');
class(B)
ans = 'uint8'
4.特定范围内的随机数
本示例显示如何基于开区间 (50, 100) 内的均匀分布创建随机浮点数组。在默认情况下,rand 返回均匀分布的归一化值(0 和 1 之间)。要改变分布的范围(a、b),应将各值乘以新范围的宽度(b – a),然后用 a 替换各值。首先,初始化随机数生成器,以使本示例中的结果具备可重复性。
rng(0,'twister');
创建一个 1000 个随机值的向量。使用
rand
函数从开区间 (50,100) 抽取均匀分布的值。
a = 50;
b = 100;
r = (b-a).*rand(1000,1) + a;
验证
r
中的数值是否在指定范围内。
r_range = [min(r) max(r)]
r_range =
50.0261 99.9746
结果是处于开区间(50、100)内。
注意 a 和 b 的某些组合在理论上可使得到的结果包括 a 或 b。在实际中,这种情况极难出现。
5.随机整数
此示例说明了如何根据一组数字 –10、–9、...、9、10 的离散均匀分布创建随机整数值数组。
最简单的
randi
语法将返回 1 与指定值
imax
之间的双精度整数值。要指定其他范围,请结合使用
imin
和
imax 参数。首先,初始化随机数生成器,以使本示例中的结果具备可重复性。
rng(0,'twister');基于数字集 -10、-9、...、9、10 的离散均匀分布创建 1×1000 随机整数值数组。使用语法
randi([imin
imax],m,n)。
r = randi([-10 10],1,1000);
验证 r
中的值是否在指定范围内。
[rmin,rmax] = bounds(r)
rmin = -10
rmax = 10
6.具有特定均值和方差的正态分布随机数
此示例说明如何基于均值为 500 和方差为 25 的正态分布创建随机浮点数组。randn 函数返回一个均值为 0 和方差为 1 的正态分布随机数样本。随机变量的一般理论规定,如果 x 是随机变量,其均值是 且方差是
且方差是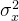 ,则由
y
=
ax
+
b
,
(其中 a 和 b 为常量)定义的随机变量 y 有均值
,则由
y
=
ax
+
b
,
(其中 a 和 b 为常量)定义的随机变量 y 有均值
rng(0,'twister');
基于均值为 500 且标准差为 5 的正态分布创建包含 1000 个随机值的向量。
a = 5;
b = 500;
y = a.*randn(1000,1) + b;
计算样本均值、标准差和方差。
stats = [mean(y) std(y) var(y)]
stats = 1×3
499.8368 4.9948 24.9483
均值和方差并非恰好为 500 和 25,因为它们是从分布采样计算得出的。
7.球体内的随机数
此示例说明如何在球体内创建随机点。本例中的球体以原点为中心,半径为3。在球体内创建点的方法之一是在球面坐标中指定这些点。然后可以将其转换为笛卡尔坐标进行绘图。首先,初始化随机数生成器,以使本示例中的结果具备可重复性。
rng(0,'twister')
计算球体中各个点的仰角。这些值在开区间 ( −
π
/2,
π
/2)
内,但不是均匀分布的。
rvals = 2*rand(1000,1)-1;
elevation = asin(rvals);
为球体中的各个点创建方位角。这些值在开区间 (0, 2
π
)
内均匀分布。
azimuth = 2*pi*rand(1000,1);
为球体中的各个点创建半径值。这些值在开区间 (0, 3)
内,但不是均匀分布的。
radii = 3*(rand(1000,1).^(1/3));
转换为笛卡尔坐标并绘制结果。
[x,y,z] = sph2cart(azimuth,elevation,radii);
figure
plot3(x,y,z,'.')
axis equal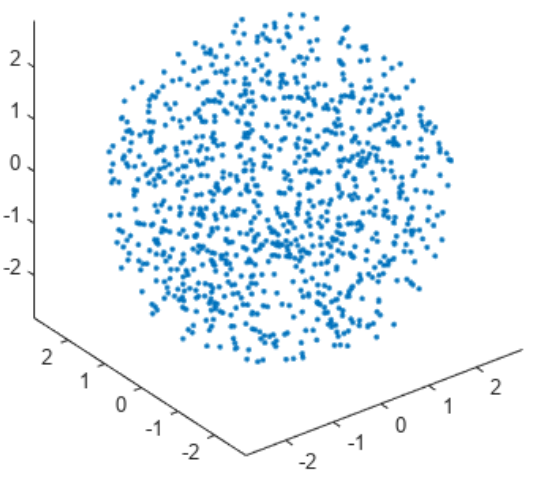
如果需要将随机数置于球体表面上,则指定一个常量半径值作为 sph2cart 的最后一个输入参数。在本例中,该值为
3
。
[x,y,z] = sph2cart(azimuth,elevation,3);