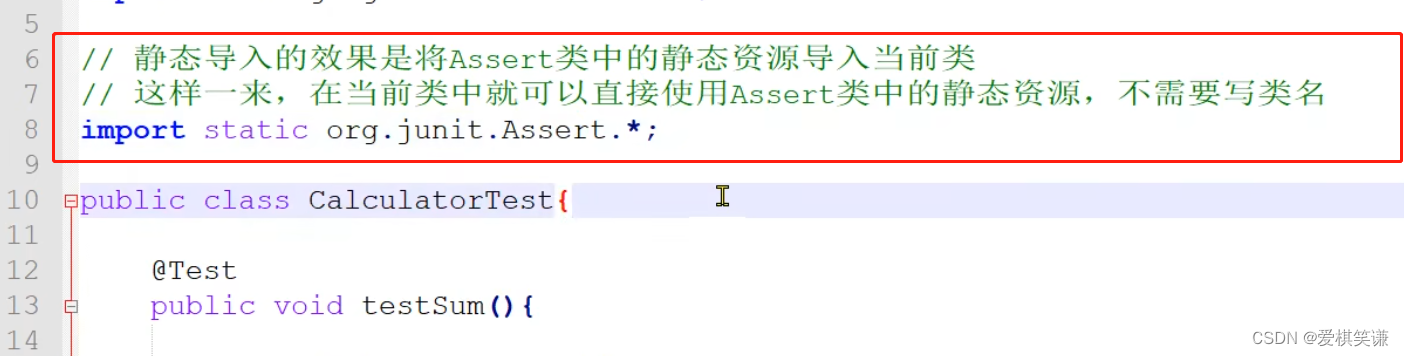
刷题历程
- - - - 基本数据结构 - - -
- 数组、字符串、堆、栈、队列、链表
- 739.每日温度(栈)
- 155. 最小栈
- 20. 有效的括号
- 581.最短无序连续数组
- 169. 多数元素(数组)
- 136.只出现一次的数字
- 128.最长连续序列
- 560.和为k的子数组(组+哈希表)
- 394 字符串解码(辅助栈)
- 283 移动零(双指针)
- 239 滑动数组最大值(大顶堆/队列)
- 84. 柱状图中最大的矩形
- 215.数组中的第K个最大元素(堆/快排)
- 208.实现Trie(前缀树)
- 647.回文子串(中心扩展法、动态规划法)
- 234.回文链表
- 160. 相交链表
- 142.环形链表
- 19. 删除链表的倒数第 N 个结点
- 2. 两数相加
- 树、图
- 617.合并二叉树
- 543.二叉树的直径
- 538.二叉搜索树转换为累加树
- 297.二叉树的序列化和反序列化
- 236. 二叉树的最近公共祖先
- 226.反转二叉树
- 124.二叉树中最大路径和
- 102. 二叉树的层序遍历
- 101.对称二叉树
- 114.二叉树展开为链表
- 98.二叉树是否为二叉搜索树
- 96. 不同的二叉搜索树
- 树总结
- 399.除法求值(图论题目)
- 207. 课程表(拓扑排序-图)
- 200 岛屿的数量
- 四大算法思想
- 回溯法(*)
- 301 删除无效的括号(困难题)
- 22. 括号生成(回溯法-深度优先+剪枝) -- 着重理解
- 79. 单词搜索
- 78.子集
- 39.组合总合
- 46.全排列
- 39. 组合总和
- 17. 电话号码的字母组合
- 遍历的总结:
- 动态规划(*)
- 494.目标和/416.分割等和子集(01背包问题) -- 复习重点
- 322零钱兑换(完全背包问题)--复习重点(需要搞清楚如何从2维数组变为1维,这个转化过程符合常规,以及循环顺序变化,循环遍历逆序的影响)
- 279 完全平方数(完全背包问题)
- 338 比特位计数
- 337打家劫舍
- 198 打家结舍
- 312戳气球(太难了,学习思路)
- 309. 最佳买卖股票时机含冷冻期(股票问题)
- 300.最长递增子序列
- 221.最大正方形
- 152 乘积最大子数组
- 139.单词拆分
- 64.最小路径和
- 62.不同的路径
- 53. 最大子数组和
- 5.最长回文字串
- 贪心
- 55.跳跃游戏
- 分治
- 快排和归并排序
- - - - 技巧题 - - -
- 技巧训练(可能使用上面结构和算法+某种技巧)
- 437. 路径总和 III(树先序遍历+前缀和思想/双递归(遍历)树思想)
- 621.任务调度器
- 438.找到字符串中所有字母异位词(经典滑动窗口)
- 3. 无重复字符的最长子串
- 406. 根据身高重建队列(数对,先排序)
- 347. 前 K 个高频元素
- 287 寻找重复数
- 240. 搜索二维矩阵 II
- 238 除自身以外数组乘积
- 75 颜色分类
- 56. 合并区间
- 49. 字母异位词分组
- 48. 旋转图像
- 31. 下一个排列
- 15. 三数之和
- 11. 盛最多水的容器
- 二分查找
- 34. 在排序数组中查找元素的第一个和最后一个位置
- 33. 搜索旋转排序数组
- 一些额外总结
- 数组问题可以借助空间来做优化时间;
- 面试 :
- 完全背包问题的里外层循环可以交换吗?
- 面试前需要复习
注:个人复习使用
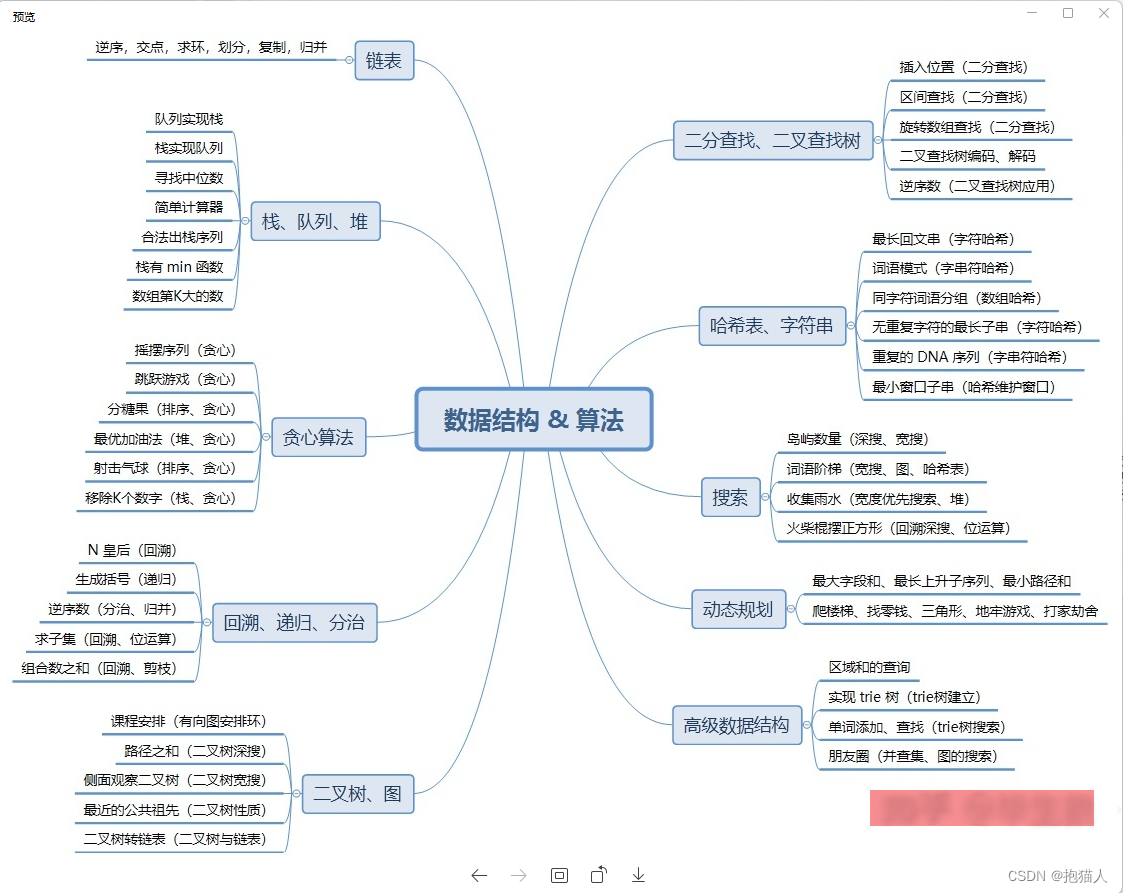
- - - 基本数据结构 - - -
数组、字符串、堆、栈、队列、链表
739.每日温度(栈)
155. 最小栈
(1)使用辅助栈,辅助栈存最小值。
(2)不能使用额外空间,栈中存差值。
20. 有效的括号
581.最短无序连续数组
169. 多数元素(数组)
找超过一半的数字,使用抵消法;遍历数组,初始第一个数为参考对象,下一个数不等于参考对象,则减去1,如果值为0则更新参考对象为下一个数。
136.只出现一次的数字
位运算(异或)。
注意,这里又多了一种新的处理数组的方式,位运算
128.最长连续序列
560.和为k的子数组(组+哈希表)
394 字符串解码(辅助栈)
283 移动零(双指针)
239 滑动数组最大值(大顶堆/队列)
队中插入一个元素:从下往上堆化
删除堆中一个元素:从上往下堆化
84. 柱状图中最大的矩形
单调栈,找左右边界(即宽的长度);
核心思想:对于某条边,利用单调栈,小于其高度,不扩展,大于等于高度才扩展;
该类型柱状图题,某条边受旁边两条边的影响时,才可考虑单调栈的方法去处理。
队列的存储最大值(单调队列)
本题的最优解是使用队列(单调递减队列,队列中保存数组下标),当窗口滑动时:
1.当队头不在窗口中时,移除掉队头(保证了队列中所有元素在窗口中)。
2.将新加入的数和队尾比较,如果队尾元素比其小,则去掉队尾元素,直到遇到比其更大值,或队列为空。
单调队列、单调栈
适合处理最值边界问题,例如滑动窗口中的最大值就用单调递减队列,确保堆头是最大值,如果队头不在窗口中就移除掉;再例如柱状图中最大的矩形,通过单调递增栈来找宽的左右边界。
215.数组中的第K个最大元素(堆/快排)
该题,重点掌握如果根据数组创建堆。
根据数组创建堆,两种方式:
(1)从下往上堆化,初始化认为堆中没有数据,依次遍历数组,然后一个一个插入
(2)从非叶子节点开始n/2(完全二叉树非叶子节点都是从n/2开始),至第一个节点,从上往下堆化。
208.实现Trie(前缀树)
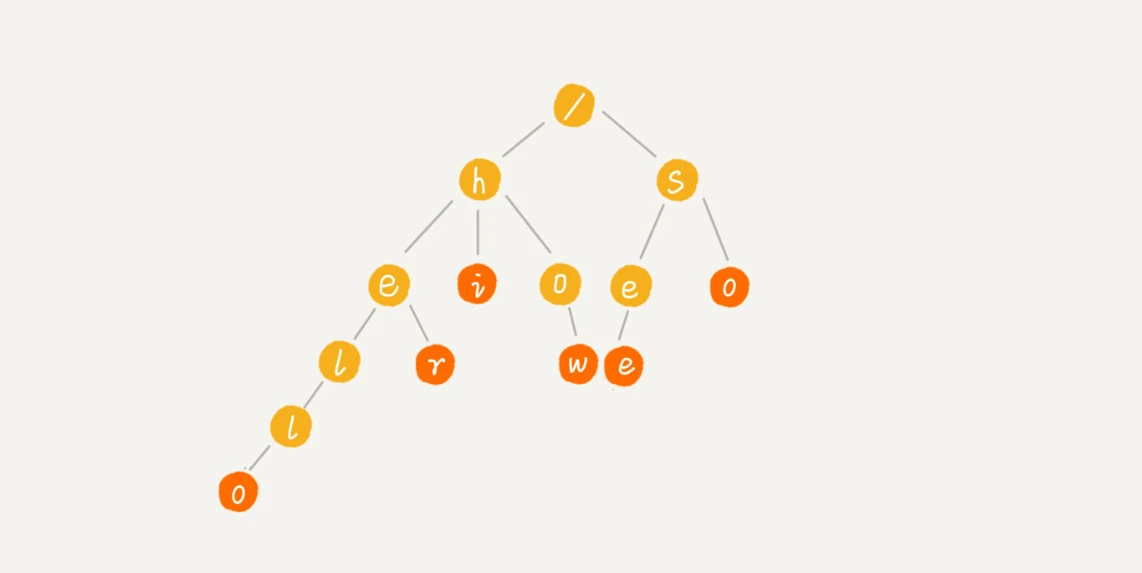
搞懂什么是Trie,字符串匹配树。例如,由how,hi,her,hello,so,see六个单词组成的trie,如下:
class TrieNode {
TrieNode *children[26];
bool isEnd;
}
647.回文子串(中心扩展法、动态规划法)
234.回文链表
空间复杂度为1:从中间反转链表再比较是否回文。
160. 相交链表
双指针,PA和PB,PA走到终点,将PA指向链表Bhead,PB走到终点,将PB指向链表Ahead,如果两者相遇即为交点;
类似问题,可以画图,列公式找规律。
链表环检测:快慢指针
142.环形链表
快慢指针检测是否存在环,若存在则必定在环中相遇;
相遇后再使用一个指针从链表头开始往后走,必定和慢指针相聚于环头
19. 删除链表的倒数第 N 个结点
直接计算链表的长度;
或者通过栈的特性来做
2. 两数相加
树、图
617.合并二叉树
543.二叉树的直径
538.二叉搜索树转换为累加树
转换为求树的高度思想。
树的题目:https://leetcode.cn/problems/convert-bst-to-greater-tree/solutions/215216/yi-tao-quan-fa-shua-diao-nge-bian-li-shu-de-wen-5/
297.二叉树的序列化和反序列化
核心还是要理解递归的思想,遍历树的方式来构造树。
236. 二叉树的最近公共祖先
递归遍历法:后续遍历,核心还是要理解树的遍历(例如,先序在代码中是表现先对访问节点处理,再处理左节点,再处理右节点)
226.反转二叉树
核心:后序遍历
124.二叉树中最大路径和
102. 二叉树的层序遍历
树的BFS访问,
BFS访问延伸的问题:bfs->层序遍历(在bfs基础上增加一个循环来处理每一层)-> 最短路径问题
101.对称二叉树
非常见的三种序列的访问方式(中序、先序、后序),而是一种如下代码的访问方式:
dfs(left->left, right->right) || dfs (left->right, right->left)
由此可见,递归去访问整个树是很灵活的。
114.二叉树展开为链表
98.二叉树是否为二叉搜索树
114和98有点类似,都可以通过找当前的节点的前驱节点来做(不同的根据题意遍历的顺序不一样,注意如果因为某些操作导致树的结构发生变化,例如114题,要根据变化做特殊处理)。
1.可以用一个全局变量来记录前驱节点。然后利用遍历树的思想。
2.如果不用全局变量来做记录,则复杂的多,例如114题中利用的是,前序遍历,左子树最右边节点是右子树的第一个节点的前驱节点。
96. 不同的二叉搜索树
动态规划题
g(n)=g(j-1)*(i-j)
树总结
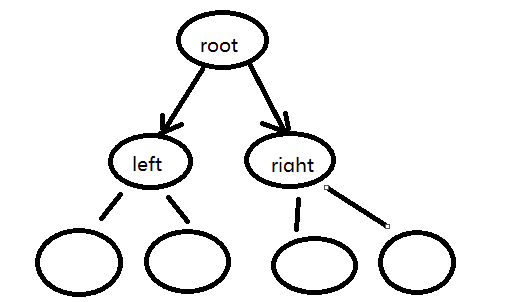
做树相关题目,首先想到的应该是是否可以通过遍历解决,如果遍历能够解决,又分两种:
1.是否通过DFS解决,如果是,采用递归的方式;根据递归顺序,又需分三种情况,先序、中序、后序。
2.是否通过BFS解决,如果是,采用队列来处理,一层一层来。
分析递归时,可以通过小树模型来思考三种顺序的递归过程(递归的精髓是,从小树可以递推大树):
399.除法求值(图论题目)
<带权并查集>
并查集要点:
刚开始所有节点都是分散的,自己管理自己;
不断的查找节点(两个节点是否有共同的头节点,优化,压缩树高度),合并节点(按照某种方式来合并,具体情况具体分析,带权图需要特定的公式)来构建一个并查集的树;
通过特定的方式不断查找和合并来构建一颗扁平的树,并查集的特定在于,处理一些不相交集合(关键字是集合,处理业务的基础是集合,而不是树,只是通过某些方法最终形成了一棵树)的合并及查询问题(效率更高)。
207. 课程表(拓扑排序-图)
** 图的实现**
(1)邻接矩阵法
顶点与顶点之间的关系使用二维数组来表示,如果说顶点i指向顶点j,则matrix[i][j] = 1(如果是带权图,则这个值可以是权值);
(2)邻接表存储法
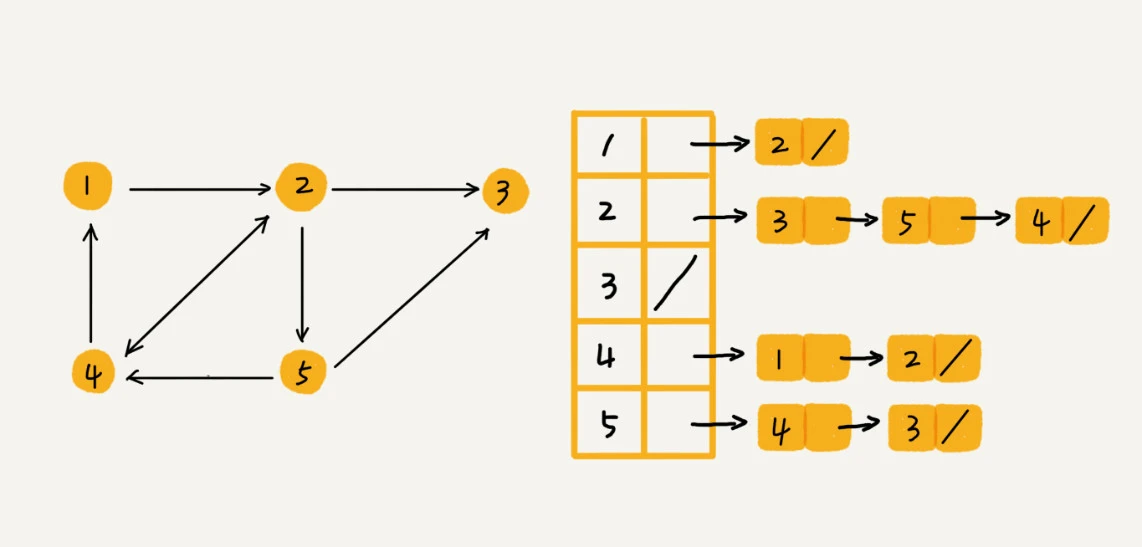
改进:后面链表过长,可考虑使用跳表、红黑树、散列表等做优化
图的搜索
方法1:BFS
广度优先搜索的空间消耗主要在几个辅助变量 visited 数组(bool数组,已经拜访过的顶点,必须要有)、queue 队列(广度优先,一层一层入队,必须有)、prev 数组上(访问关系,最终通过这个数组来整理出搜索路径)。这三个存储空间的大小都不会超过顶点的个数,所以空间复杂度是 O(V)。
方法2:DFS
深度优先遍历使用的核心思想是回溯。
for(i:图的顶点)
{
if(visit(i) == 0)
dfs(i)
}
图的遍历都需要记录每个顶点是否被遍历过,避免同一个顶点被遍历两次。
拓扑排序不用区分什么广度优先深度优先把自己弄乱了,抓住节点入度和出度的本质特征。 方法一: 从入度思考(从前往后排序), 入度为0的节点在拓扑排序中一定排在前面, 然后删除和该节点对应的边, 迭代寻找入度为0的节点。 方法二: 从出度思考(从后往前排序), 出度为0的节点在拓扑排序中一定排在后面, 然后删除和该节点对应的边, 迭代寻找出度为0的节点。
拓扑排序
方法1:Kahn 算法
如果A需要在B之前完成,则让A指向B,如果说某个顶点的入度为零,则可以让其输出排序(移除掉);循环上述操作,直到所有顶点都输出排序。
200 岛屿的数量
方案1:遇到1后,深度优先搜索/广度优先搜素,将遇到的1全部修改为0,记录需要搜索的次数。
方案2:并查集解题。
a.初始每个的节点(每个节点都是自己集)
b.合并节点(先查找两个集的公共祖先(查找的过程中可以压缩),在合并两个集)
四大算法思想
回溯法(*)
301 删除无效的括号(困难题)
排列组合思想,从N个数中取出M个数组合(M<N),使用循环中递归的方式回溯(核心思想,理解,和常见的回溯明面上不太一样)。
回溯一定要配合剪枝使用。
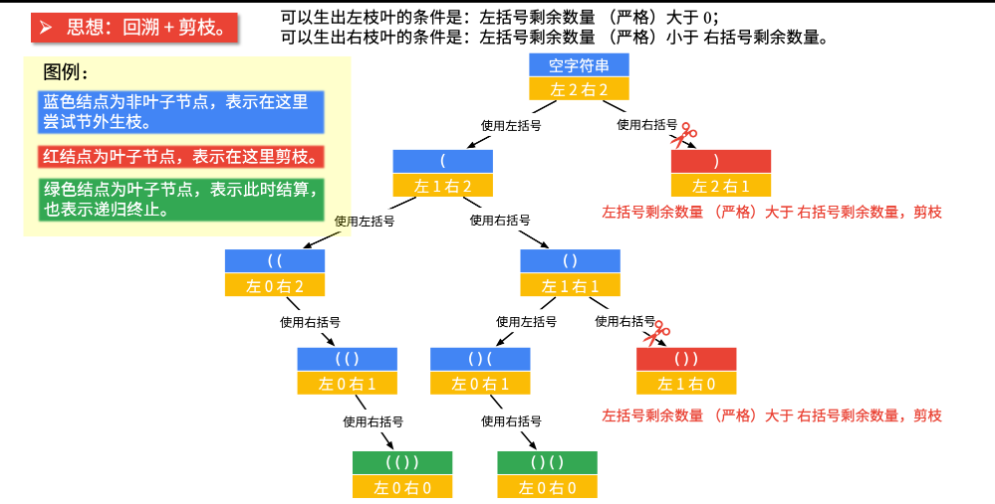
22. 括号生成(回溯法-深度优先+剪枝) – 着重理解
核心思想:可生成左枝叶树,左括号的剩余数量大于0;可生产右枝叶树,左括号的剩余数量小于右括号的剩余数量。
import java.util.ArrayList;
import java.util.List;
public class Solution {
// 做减法
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<>();
// 特判
if (n == 0) {
return res;
}
// 执行深度优先遍历,搜索可能的结果
dfs("", n, n, res);
return res;
}
private void dfs(String curStr, int left, int right, List<String> res) {
// 因为每一次尝试,都使用新的字符串变量,所以无需回溯
// 在递归终止的时候,直接把它添加到结果集即可
if (left == 0 && right == 0) {
res.add(curStr);
return;
}
// 剪枝(如图,左括号可以使用的个数严格大于右括号可以使用的个数,才剪枝,注意这个细节)
if (left > right) {
return;
}
if (left > 0) {
dfs(curStr + "(", left - 1, right, res);
}
if (right > 0) {
dfs(curStr + ")", left, right - 1, res);
}
}
}
79. 单词搜索
深度优先+回溯法,注意深度优先遍历网格时需要记录已经遍历过的位置,避免重复遍历。
78.子集
(1)回溯法,回溯的思想与301相似,多个选择时循环都尝试:
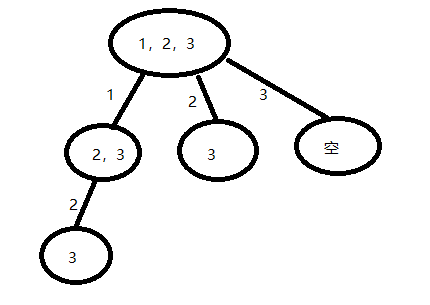
(2)递归法:
选或者不选,构建一棵二叉树
39.组合总合
和78类似,不同的是数据可以多次重复取;注意,在回溯法中,如果出现了由于顺序不同导致的重复子序列,要使用剪枝:具体的做法是每一次搜索时设置下一轮搜索的起点。
回溯问题需要注意的是,回溯到某个节点时,状态也要恢复到刚来这个节点时。
46.全排列
经典回溯题。
39. 组合总和
回溯+剪枝
17. 电话号码的字母组合
遍历的总结:
深度优先:递归(栈),一直往里走,走到底返回,例如,二叉树的递归遍历。
广度优先:队列,一排一排的走,例如,一层一层的遍历树。
注意:理解树的遍历和回溯法中深度优先遍历的联系,从宏观的角度去看待两者的联系;最终还是理解递归的本质是从上往下走,走到底再返回,可以借鉴二叉树来理解递归(比如说,中序遍历二叉树时,递归函数需要调用两次,路线是怎么走的)
回溯和动态规划的区别: 动态规划以求最有解为主,而回溯则是所有的方案。
动态规划(*)
dp三要素,定义状态(定义方程式),初始状态(初始化),状态转移(小问题解推大问题解)
注:背包问题复习重点,1.01背包和完全背包公式理解 2.优化滚动数据 (优化时01和完全是否都要逆序遍历) 3.多层循环是否可以交换顺序 4.用递归,从上往下的思路写伪代码。
01背包的状态转移方程为:dp(i,j)=max(dp(i-1,j),dp(i-1,j-v[i])+val[i])
完全背包的状态转移方程:dp(i,j)=max(dp(i-1,j),dp(i,j-v)+val[i])
494.目标和/416.分割等和子集(01背包问题) – 复习重点
01背包类型问题,2个点:
1.利用递归从上往下分解时,最下层有N中可能(区别斐波那契数列,最下面只有一种情况);
2.写转移方程式时,注意数组二维取值范围是否需要注意负数情况(是否可以转化为多个整数相加和为某个值的情况)。
动态规划详解:https://blog.csdn.net/wat1r/article/details/114377702?spm=1001.2014.3001.5501
作为「0-1 背包问题」,它的特点是:「每个数只能用一次,容量有限制」。解决的基本思路是:物品一个一个选,容量也一点一点增加去考虑,这一点是「动态规划」的思想,特别重要。
容量限制的思考:对于01背包来说,容量是固定的;对于目标和来说,容量等价于([-sum,sum])),虽然和是一个定值,但是求解的结果可能千千万万,只取其中满足定值和的,因此不能用定制和来做容量。总的来说,具体问题具体分析。
优化:滚动数组
322零钱兑换(完全背包问题)–复习重点(需要搞清楚如何从2维数组变为1维,这个转化过程符合常规,以及循环顺序变化,循环遍历逆序的影响)
279 完全平方数(完全背包问题)
注意,这种问题的条件是一个固定的值,与容量和利益问题相比要简单些,容量和利益问题中条件容量是不固定的。
容量固定了,很多可以用一维数组来解答(注意这里的一维数组不是滚动数组的优化成一维数组,而是本身的思路就是一维来做的)。
338 比特位计数
Brian Kernighan算法: n & ( n - 1 ) 删除最右侧的1(注意最右侧的意思是指,从左往右数第一个1)
注意,一个整数n有log2n位(即位数N=log2n),因此处理整数的位数时间复杂度位logn
动态规划::
bits[x]=bits[x>>1]+(x & 1)
这种类型的题目(位计算),主要是要找到数与数之间位的关系。
337打家劫舍
二叉树的遍历+动态规划
这里将树的遍历和动态规划结合了,常做题的动态规划是用for循环去循环数组,但是该题是遍历树,因此用到了递归树遍历方式配合动态方程式。
198 打家结舍
动态方程:
dp[0]=nums[0]
dp[1]=max(nums[0],nums[1])
312戳气球(太难了,学习思路)
309. 最佳买卖股票时机含冷冻期(股票问题)
300.最长递增子序列
使用贪心+二分查找核心思想(思维训练):使用一个临时数组来保存最长子序列,遍历原序列:1.如果当前数据都大于临时数组,则添加到临时数组最后面。2.如果当前数据小于临时数组中的数,则使用当前数据去覆盖临时数组中比他大的最小的那个。临时数组不一定是原数组中真实的有序数组,但一定是最长的。
使用动态规划,for i := 0->nums.len for j := 0->i { if(num[i ] > num[ j]) dp[i] = max(dp[i], dp[j] + 1);}
221.最大正方形
公式:f[i][j]=min(f[i][j−1],f[i−1][j],f[i−1][j−1])+1, f[i][j]表示以i,j为右下角正方形的最大边长
152 乘积最大子数组
乘积问题:当遇到负数时,最大值变最小值,最小值变最大值
139.单词拆分
64.最小路径和
可以对比01背包问题理解该种题型:思维上倒过来推导,想要知道f(x)的最值,就必须要f(x-1),所以需要列举出所有情况。
62.不同的路径
同64
53. 最大子数组和
本题也可以使用分治算法来做,涉及到一个线段树的概念。
5.最长回文字串
1.使用动态规划求解,d[i][j] = d[i] == d[j] && d[i+1][j-1]
动态规律,分别求长度为1、2、3…n(s.length())的字符串是否为回文。
2.中心扩散算法(注意,有两种情况,奇数时中心是一个数,偶数时中心是两个数)
贪心
55.跳跃游戏
分治
快排和归并排序
一个是自上而下的分治(快排),一个是自下而上的分治(归并)。
- - - 技巧题 - - -
技巧训练(可能使用上面结构和算法+某种技巧)
437. 路径总和 III(树先序遍历+前缀和思想/双递归(遍历)树思想)
前缀和:a[n -> m] = s[m] - s[n] s[n]表示前n个数的和
621.任务调度器
438.找到字符串中所有字母异位词(经典滑动窗口)
下图代码比较经典的解释滑动窗口(下面采用窗口伸缩,官方解答1用的固定窗口):
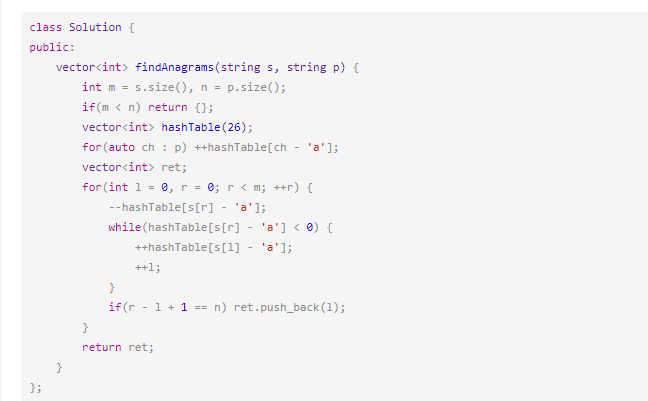
注:题解热度2中,用户labuladong归纳了多个滑动窗口相关题目
滑动窗口模板式答题:
int left = 0, right = 0;
while (right < s.size()) {
// 增大窗口
window.add(s[right]);
right++;
while (window needs shrink) {
// 缩小窗口
window.remove(s[left]);
left++;
}
}
3. 无重复字符的最长子串
406. 根据身高重建队列(数对,先排序)
347. 前 K 个高频元素
1.使用哈希表记录每个元素出现得频次;
2.使用大小为K得小顶堆来处理哈希表/快速排序查找数组中第K大的元素(O(n))。
287 寻找重复数
思路一:二分法变形
二分法的变形,很有技巧,核心思想:n+1的数组放n个数,其中必定有一个数重复了;我们假定有一个已经排序好的数组,数组按顺序存放数字1至n,使用二分法找到这个数组的mid值,然后遍历原数组(n+1个值的数组),根据原数组中大于mid值数字的数量来确定下一次二分查找的左边界或有边界。
这个技巧实质上就是查找一个排序好的数组的数,但是每次查找的边界都从其他数组中来确定(这两个数组需要一定的关联),可谓是灵活运用二分法了(^ - ^)。
思路二:闭环链表(很不容易想到,但是复杂度为O(n))
闭环链表是一种典型可使用快慢指针解决的问题。快慢指针的核心是:快指针每次走两步,慢指针每次走一步,如果有环快指针肯定能追上慢指针。
核心思想:将这个题目给的特殊的数组当作一个链表来看,把数组的元素看作指针。如nums[0]中的值为1,nums[0] 指向数组下标为1的元素。以数组[1,3,4,2]为例,arr[0]==1 -> arr[1]。
然后分2步(具体细节看leetcode):
1.数组中有一个重复的整数 = 链表中存在环
2.找到数组中的重复整数 = 找到链表的环入口
240. 搜索二维矩阵 II
从左至右,从上到下一次递增的矩阵中找一个数字,从右上角开始找(Z字型)。
238 除自身以外数组乘积
左右乘积列表的方式。
对数组的处理:
加法,前缀和;
乘法,左右乘积列表;
75 颜色分类
双指针问题
56. 合并区间
先排序,再合并
49. 字母异位词分组
哈希,通过对字母的数量计数后哈希,此题算是对哈希的一个技巧练习
48. 旋转图像
先对折,在斜对折,技巧题,数学推理。
31. 下一个排列
1.从后向前 查找第一个 相邻升序 的元素对 (i,j),满足 A[i] < A[j]。此时 [j,end) 必然是降序
2.在 [j,end) 从后向前 查找第一个满足 A[i] < A[k] 的 k。A[i]、A[k] 分别就是上文所说的「小数」、「大数」
3.将 A[i] 与 A[k] 交换
4.可以断定这时 [j,end) 必然是降序,逆置 [j,end),使其升序
5.如果在步骤 1 找不到符合的相邻元素对,说明当前 [begin,end) 为一个降序顺序,则直接跳到步骤 4
15. 三数之和
关键点:
1.数组排序,方便去重(循环时,如果值和上一次循环相同则跳过)
2.将second、third循环合并为一个循环(核心,使用双指针,本质变为一个循环);
3.num[first] > 0 ,直接结束(后面都是大于0的)
4.num[second] + num[third] + num[first] 大于0,则third太大,减减third;反之,second太小,加加second。等于0时,则保存三个值到结果,继续加加second找下一轮。(first/second/third分别表示循环)
11. 盛最多水的容器
双指针解题(15题也是这个思想),双指针的核心在于把两次for循环缩减为一次for循环,但是前提是要题意要符合双指针解法(即该题可以用一前一尾两个指针朝中间移动来得到题解)。
二分查找
//最基本的,变形在此基础上更改,主要是找下一个l或者r
while(l <= r)
{
mid = l + ((r - l ) >> 1);
if(arr[mid] == target) return mid;
if(arr[mid] > target)
{
r = mid - 1;
}
else
{
l = mid + 1;
}
}
34. 在排序数组中查找元素的第一个和最后一个位置
33. 搜索旋转排序数组
mid的左右肯定有一个是有顺序的,通过这个来判断l和r的走向。
一些额外总结
数组问题可以借助空间来做优化时间;
二叉搜索树中序遍历,即为有序(从小到大)的一个集合。
面试 :
https://programmercarl.com/%E5%89%8D%E5%BA%8F/%E7%A8%8B%E5%BA%8F%E5%91%98%E7%AE%80%E5%8E%86.html#%E9%A1%B9%E7%9B%AE%E7%BB%8F%E9%AA%8C%E5%BA%94%E8%AF%A5%E5%A6%82%E4%BD%95%E5%86%99
完全背包问题的里外层循环可以交换吗?
背包的内外循环是否可以交换,关键看内部循环是否可以从左往右遍历;
01背包问题,使用二维数组,可以交换,优化为一维数组,不能交换(因为内循环必须是从右到左);
完全背包问题,使用二维数组和优化后的一维数组都可以交换。
内外交换意味着二维数组的横向初始化和纵向初始化的交换;
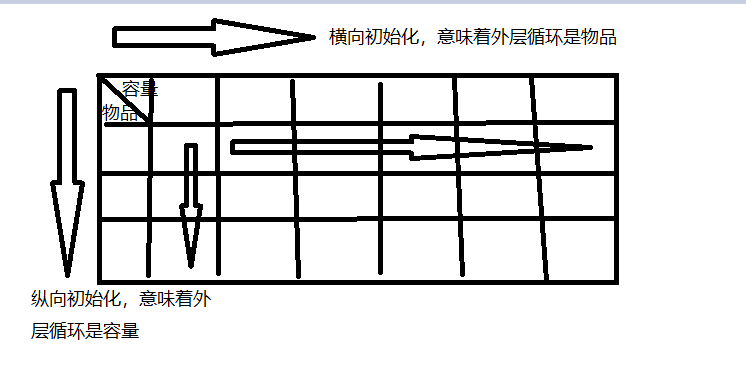
链接有详细解释:https://blog.csdn.net/weixin_57023347/article/details/119301152?ops_request_misc=&request_id=&biz_id=102&utm_term=%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduweb~default-0-119301152.nonecase&spm=1018.2226.3001.4187
面试前需要复习
1.动态规划之01背包问题(01背包->完全背包->滚动优化->上面提到的细节)
2.排序算法·
3.滑动窗口问题
4.并查集
5.回溯法







![[golang gin框架] 45.Gin商城项目-微服务实战之后台Rbac微服务之角色权限关联](https://img-blog.csdnimg.cn/1aeb9c46b93542638866a62a44df0410.png)