最优化：建模、算法与理论

目前在学习 最优化：建模、算法与理论这本书，来此记录一下，顺便做一些笔记，在其中我也会加一些自己的理解，尽量写的不会那么的条条框框（当然最基础的还是要有）

第二章 基础知识

2.1 范数

2.1.1 向量范数

定义2.1（范数）称一个从向量空间Rⁿ到实数域R的非负函数||·||为范数，如果他满足：
（1）正定性：对于所有的$v\in R^n$，有$||v||>=0$,且 $||v||=0$ 当且仅当 $v=0$
（2）齐次性：对于所有的$v\in R^n$和$\alpha \in R$，有$||\alpha v||$=$|\alpha |$ $||v||$
（3）三角不等式：对于所有的$v,w\in R^n$,有$||v+w||<=||v||+||w||$
最常用的向量范数为l_p范数（p >= 1）
$$||v|{|}_p=(|v_1{|}^p+|v_2{|}^p+\dots +|v_n{|}^p{)}^{1/p}$$

显而易见，高数应该都学过，如果$p=\infty$，那么$l_{\infty }$范数定义为$$||v|{|}_{\infty }=max|v_i|$$

记住 $p=1,2,\infty$的时候最重要，有时候我们会忽略$l_2$范数的角标
也会遇到由正定矩阵$A$诱导的范数，即$||x|{|}_A=\sqrt{x^{T}Ax}$

对于$l_2$范数，有常用的柯西不等式，设$a,b\in R^n$，则
$$|a^{T}b|<=||a|{|}_2||b|{|}_2$$
等号成立当且仅当a与b线性相关

2.1.2 矩阵范数

矩阵范数首先也一样要满足那三个特性啦，就是要满足正定性，齐次性，三角不等式，常用的就是$l_1,l_2$范数，当$p=1$时，矩阵$A\in R^{m\ast n}$的范数定义
$$||A|{|}_1=\sum _{i=1}^m\sum _{j=1}^n|a_{ij}|$$
当$p=2$时，也叫矩阵的Frobenius范数（F范数），记为$||A|{|}_F$，其实就是所有元素的平方和然后开根号，具体定义如下
$$||A|{|}_F=\sqrt{Tr(A{A}^T)}=\sqrt{\sum _{i,j}{a}_{ij}^2}$$
这里的$Tr$表示方阵X的迹（这个大家应该都知道吧，我把百度的解释搬过来—在线性代数中，一个n×n矩阵A的主对角线（从左上方至右下方的对角线）上各个元素的总和被称为矩阵A的迹（或迹数），一般记作tr(A)），矩阵的F范数具有正交不变性。
正交不变性呢就是说对于正交矩阵$U\in R^{m\ast n},V\in R^{m\ast n}$，我们有
$$||UAF|{|}_F^2=||A|{|}_F^2$$
具体的推导我这里就不写了哈，打公式太麻烦了哈哈，感兴趣的可以看这本书的第24页或者来找我^^

矩阵范数也可以由向量范数给诱导出来，一般称这种算数为诱导范数，感觉用的不是很多，这里先不扩展开了
除了上诉的1范数，2范数，另一个常用的矩阵范数是核范数，给定矩阵$A\in R^{m\ast n}$，核范数定义为
$$||A|{|}_{\ast }=\sum _{i=1}^r{\sigma }_i$$
其中${\sigma }_i,i=1,2,...,r$为$A$的所有非0奇异值,$r=rank(A)$，类似于向量的$l_1$范数可以保稀疏性，我们也通常通过限制矩阵的核范数来保证矩阵的低秩性。

2.1.3 矩阵内积

内积一般用来表征两个矩阵之间的夹角，一个常用的内积—Frobenius内积，$m\ast n$的矩阵$A$和$B$的Frobenius内积定义为
$$<A,B>=Tr(A{B}^T)=\sum _{i=1}^m\sum _{j=1}^n{a}_{ij}{b}_{ij}$$
其实就是两个矩阵一一对应元素相乘
同样的，我们也有矩阵范数对应的柯西不等式，设$A,B\in R^{m\ast n}$，则
$$|<A,B>|<=||A|{|}_F||B|{|}_F$$
等号成立当且仅当A和B线性相关

2.2 导数

2.2.1 梯度与海瑟矩阵

梯度的定义（这玩意应该是我之前好像都没见到过的）：给定函数$f:R^n\to R$，且$f$在点$x$的一个邻域内有意义，若存在向量$g\in R^n$满足
$$\underset{p\to 0}{\lim }\frac{f(x+p)-f(x)-g^{T}p}{||p||}=0$$
就称$f$在点$x$处可微，此时$g$称为$f$在点$x$处的梯度，记作$\nabla f(x)$，如果对区域D上的每一个点$x$都有$\nabla f(x)$存在，则称$f$在D上可微

然后呢，这其中经过一系列的推导，就可以得到我们耳熟能详的梯度公式
$$\nabla f(x)={\left[\begin{array}{c}\frac{\partial f(x)}{\partial x_1}，\frac{\partial f(x)}{\partial x_2}，...,\frac{\partial f(x)}{\partial x_m}\end{array}\right]}^T$$
对于多元函数，我们可以定义其海瑟矩阵：如果函数$f(x):R^n\to R$在点$x$处的二阶偏导数$\frac{{\partial }^{2}f(x)}{\partial x_i\partial x_j}i,j=1,2,...,n$都存在，则
$${\nabla }^{2}f(x)=\left[\begin{array}{cccc}\frac{{\partial }^{2}f(x)}{\partial x_1^2}& \frac{{\partial }^{2}f(x)}{\partial x_1\partial x_2}& \cdots & \frac{{\partial }^{2}f(x)}{\partial x_1\partial x_n}\\ \frac{{\partial }^{2}f(x)}{\partial x_2\partial x_1}& \frac{{\partial }^{2}f(x)}{\partial x_2^2}& \cdots & \frac{{\partial }^{2}f(x)}{\partial x_2\partial x_n}\\ ⋮& ⋮& & ⋮\\ \frac{{\partial }^{2}f(x)}{\partial x_n\partial x_1}& \frac{{\partial }^{2}f(x)}{\partial x_n\partial x_2}& \cdots & \frac{{\partial }^{2}f(x)}{\partial x_n^2}\end{array}\right]$$
成为$f$在点$x$处的海瑟矩阵
当${\nabla }^{2}f(x)$在区域D上每个点$x$都存在，就称$f$在D上二阶可微，若他在D上还连续，可以证明此时的海瑟矩阵是一个对称矩阵
当$f:R^n\to R^m$是向量值函数时，我们可以定义他的雅可比矩阵$J(x)\in R^{m\ast n}$，他的第i行分量$f_i(x)$梯度的转置，即
$$J(x)=\left[\begin{array}{cccc}\frac{\partial f_1(x)}{\partial x_1}& \frac{\partial f_1(x)}{\partial x_2}& \cdots & \frac{\partial f_1(x)}{\partial x_n}\\ \frac{\partial f_2(x)}{\partial x_1}& \frac{\partial f_2(x)}{\partial x_2}& \cdots & \frac{\partial f_2(x)}{\partial x_n}\\ ⋮& ⋮& & ⋮\\ \frac{\partial f_m(x)}{\partial x_1}& \frac{\partial f_m(x)}{\partial x_2}& \cdots & \frac{\partial f_m(x)}{\partial x_n}\end{array}\right]$$
容易看出，梯度$\nabla f(x)$的雅可比矩阵就是f(x)的海瑟矩阵
类似于一元函数的泰勒展开，对于多元函数，这里也不加证明的给出泰勒展开
设$f:R^n\to R$是连续可微的，$p\in R^n$，那么
$$f(x+p)=f(x)+\nabla (x+tp{)}^{T}p$$
其中$0<t<1$，进一步，如果说$f$是二阶连续可微的
$$f(x+p)=f(x)+\nabla f(x{)}^{T}p+\frac{1}{2}{p}^T{\nabla }^{2}f(x+tp)p$$
其中$0<t<1$

最后呢这一章还介绍了一类特殊的可微函数-----梯度利普希茨连续的函数，这类函数在很多优化算法收敛性证明中起着关键作用
梯度利普希茨连续定义：给定可微函数$f$，若存在$L>0$,对任意$x,y\in domf$有（$domf$就是$f$的定义域）
$$||\nabla f(x)-\nabla f(y)||\le L||x-y||$$
则称$f$是梯度利普希茨连续的，相应利普希茨常数为$L$，有时候也会称为$L$-光滑，或者梯度$L$-利普希茨连续
梯度利普希茨连续表明，$\nabla f(x)$的变化可以被自变量$x$的变化所控制，满足该性质的函数有很多很好的性质， 一个重要的性质就是具有二次上界
具体证明我这里我就不再过多阐述了，有二次上界就是说$f(x)$可以被一个二次函数上界所控制，即要求说$f(x)$的增长速度不超过二次
还有一个推论就是说，如果$f$是梯度利普希茨连续的，且有一个全局最小点$x^{\ast }$，我们可以利用二次上界来估计$f(x)-f(x^{\ast })$的大小，其中$x$可以是定义域中任意一点
$$\frac{1}{2L}||\nabla f(x)|{|}^2\le f(x)-f(x^{\ast })$$
具体的证明我这里就不写了哈，想知道的可以百度或者我们讨论一下

2.2.2 矩阵变量函数的导数

多元函数梯度的定义也可以推广到变量是矩阵的情况，以$m\ast n$矩阵$X$为自变量的函数$f(X)$，若存在矩阵$G\in R^{m\ast n}$满足
$$\underset{V\to 0}{\lim }\frac{f(X+V)-f(X)-<G,V>}{||V||}=0$$
其中$||\cdot ||$是任意矩阵范数，就称矩阵向量函数$f$在$X$处$Fr\acute{a}chet$可微，就称G为$f$在$Fr\acute{a}chet$可微意义下的梯度，其实矩阵变量函数$f(X)$的梯度也可以用其偏导数表示为
$$\nabla f(x)=\left[\begin{array}{cccc}\frac{\partial f}{\partial x_{11}}& \frac{\partial f}{\partial x_{12}}& \cdots & \frac{\partial f}{\partial x_{1n}}\\ \frac{\partial f}{\partial x_{21}}& \frac{\partial f}{\partial x_{22}}& \cdots & \frac{\partial f}{\partial x_{2n}}\\ ⋮& ⋮& & ⋮\\ \frac{\partial f}{\partial x_{m1}}& \frac{\partial f}{\partial x_{m2}}& \cdots & \frac{\partial f}{\partial x_{mn}}\end{array}\right]$$
$Fr\acute{a}chet$可微的定义和使用往往比较繁琐，为此还有另一种定义-----$G\hat{a}teaux$可微
定义：设$f(X)$为矩阵变量函数，如果存在矩阵$G\in R^{m\ast n}$对任意方向$V\in R^{m\ast n}$满足
$$\underset{t\to 0}{\lim }\frac{f(X+tV)-f(X)-t<G,V>}{t}=0$$
则称$f$关于$X$是$G\hat{a}teaux$的，就称G为$f$在$G\hat{a}teaux$可微意义下的梯度
若$Fr\acute{a}chet$可微可以推出$G\hat{a}teaux$可微，反之则不可以，但这本书讨论的函数基本都是$Fr\acute{a}chet$可微的，所以我们目前无需讨论，大家了解一下就好了~，统一将矩阵变量函数$f(X)$的导数记为$\frac{\partial f}{\partial X}$或者$\nabla f(X)$

举个例子把，免得大家不知道有什么用
考虑线性函数：$f(X)=Tr(A{X}^{T}B)$，其中$A\in R^{p\ast n},B\in R^{m\ast p},X\in R^{m\ast n}$对任意方向$V\in R^{m\ast n}$以及$t\in R$，有
$$\underset{t\to 0}{\lim }\frac{f(X+tV)-f(X)}{t}=\underset{t\to 0}{\lim }\frac{Tr(A(X+tV{)}^{T}B-Tr(A{X}^{T}B))}{t}$$
$$=Tr(A{V}^{T}B)=<BA,V>$$
所以，$\nabla f(X)=BA$
我学到这里时候会有一个疑问，就是$Tr(A{V}^{T}B)=<BA,V>$是为什么呢？
我们知道，$Tr(A{V}^{T}B)=Tr(BA{V}^T)$这个是迹的基本性质，$BA$和$V$都是$m\ast n$的，那么这时候又有一个性质，假设C和D是相同规模的矩阵，那么$Tr(A^{T}B)=<A,B>$
我这里是参考知乎jordi的，这是他的一个关于3*3矩阵的推导
链接：https://www.zhihu.com/question/274052744/answer/1521521561

那么这样就可以推出$Tr(A{V}^{T}B)=Tr(V^T,BA)=<BA,V>$啦

2.2.3 自动微分

自动微分是使用计算机导数的算法，在神经网络中，我们通过前向传播的方式将输入数据$a$转化为$\hat{y}$，也就是将输入数据$a$作为初始信息，将其传递到隐藏层的每个神经元，处理后输出得到$\hat{y}$。
通过比较输出得到$\hat{y}$与真实标签y，可以定义一个损失函数$f(x)$，其中$x$表示所有神经元对饮的参数集合，$f(x)$一般是多个函数复合的形式，为了找到最优的参数，我们需要通过优化算法来调整$x$使得$f(x)$达到最小，因此，对神经元参数$x$的计算是不可避免的
这一块就是讲了一个神经网络的前向传播和后向求导，自动微分有两种方式，前向模式和后向模式，前向模式就是变传播变求导，后向模式就是前传播再一层层求导，很显然现在大家学的都是后向模式这种的吧，因为他复杂度更低，计算代价小

2.3 广义实值函数

数学分析的课程中我们学习了函数的基本概念，函数是从向量空间$R^n$到数据域$R$的映射，而在最优化领域，经常涉及到对某个函数的某一个变量取inf(sup)操作，这导致函数的取值可能为无穷，为了能更方便的描述优化问题，我们需要对函数的定义进行某种扩展。
那么 what is 广义实值函数呢？
令$\bar{R}=R\bigcup \infty$为广义实数空间，则映射$f:R^n\to \bar{R}$称为广义实值函数，可以看到，就是值域多了两个特殊的值，正负无穷

2.3.1 适当函数

适当函数：给定广义实值函数$f$和非空集合$X$，如果存在$x\in X$使得$f(x)<+\infty$，并且对任意的$x\in X$，都有$f(x)>-\infty$，那么称函数$f$关于集合$X$是适当的
总结一下，就是说适当函数$f$呢，至少有一处的取值不为正无穷，以及处处取值不为负无穷。对于最优化问题，适当函数可以帮助我们去掉一些不感兴趣的函数，从一个比较合理的函数类去考虑问题。这应该很好理解，我们加入讨论一个min问题，他至少有个取值不能为正无穷吧，要不然怎么取min，然后处处取值不能为负无穷，要不讨论有啥意义对吧？
我们约定，若本书无特殊说明，定理中所讨论的函数均为适当函数
对于适当函数$f$，规定其定义域
d o m f = { x ∣ f ( x ) < + ∞ } domf=\{x|f(x)<+{\infty}\} domf={x∣f(x)<+∞}
因为对于适当函数的最小值肯定不可能在正无穷处取到^^

2.3.2 闭函数

闭函数是另一类重要的广义实值函数，闭函数可以看作是连续函数的一种推广
在说闭函数之前，我们先引入一些基本概念：

1.下水平集

下水平集是描述实值函数取值的一个重要概念：为此有如下定义
（$\alpha$-下水平集）对于广义实值函数：$f:R^n\to \bar{R}$
C α = { x ∣ f ( x ) ≤ α } C_{\alpha}=\{x|f(x)\le{\alpha}\} Cα​={x∣f(x)≤α}
称为$f$的$\alpha$-下水平集
就是取值不能超过$\alpha$嘛，若$C_{\alpha }$非空，我们知道$f(x)$的全局最小点一定落在$C_{\alpha }$中，无需考虑之外的点

2.上方图

上方图是从集合的角度来描述一个函数的具体性质，有如下定义：
对于广义实值函数$f：R^n\to \bar{R}$
$$epif=\{(x,t)\in R^{n+1}|f(x)\le t\}$$

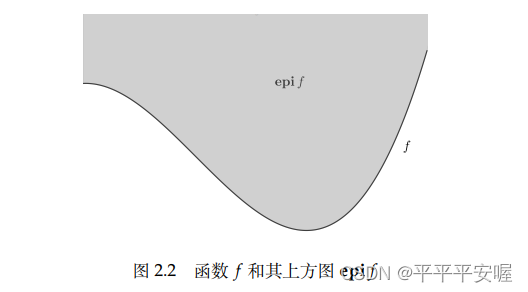
说人话就是函数$f$上方的东西小于等于t（t取任意值），$f$的很多性质都可以通过$epif$得到，可以通过$epif$的一些性质$f$的性质

3.闭函数、下半连续函数

闭函数：设$f:R^n\to \bar{R}$为广义实值函数，若$epif$为闭集，则称$f$为闭函数
下半连续函数：设广义实值函数$f:R^n\to \bar{R}$，若对任意的$x\in R^n$，有
$$\underset{y\to x}{\mathrm{liminf}}f(y)\ge f(x)$$
则$f(x)$为下半连续函数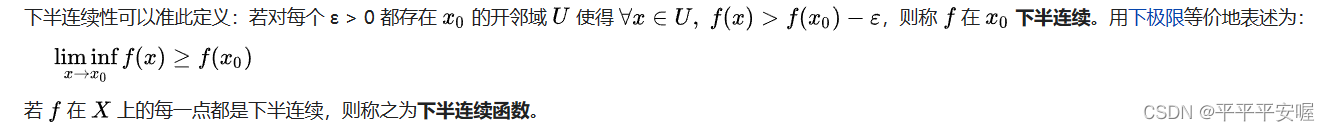

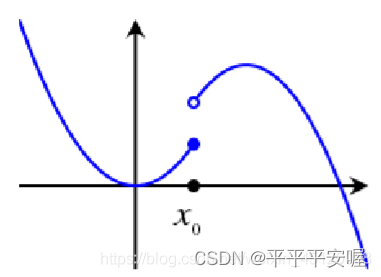
我觉得如果不懂这个下极限的话，直接看文字会好得多

其实就是在$x_0$处的邻域处，如果 f($x_0$) 减去一个正的微小值，从而可以恒小于该邻域的所有$f(x)$，则称在该间断点处有下半连续性。

如果是下图这样的

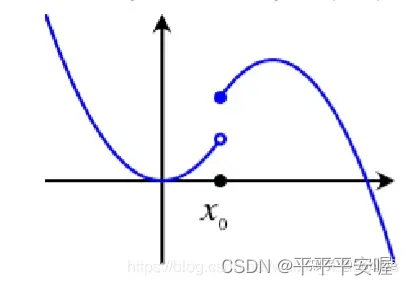
你的$x_0$再往左边取哪怕一点点，都会骤降，就达不到$x_0$的邻域中的$x$比$f(x_0)-\epsilon$大，而如果是第一张图，我们可以保证$x_0$的左边不会骤降，差不多就是这个意思

设广义实值函数$f:R^n\to \bar{R}$。则以下命题等价：
（1）$f(x)$的任意$\alpha$-下水平集都是闭集
（2）$f(x)$是下半连续的
（3）$f(x)$是闭函数
具体证明我就不在这细细展开了，同理，想知道可以和我探讨或者自行谷歌~
闭集：​ 如果对任意收敛序列，最终收敛到的点都在集合内，那么集合是闭的
我们可以看到，其实闭函数和下半连续函数可以等价，以后往往只会出现一种定义
闭（下半连续）函数间的简单运算会保持原有性质
（1）加法，若$f$和$g$均为适当的闭函数，并且$domf\bigcap domg\ne \varnothing$则$f+g$也是闭函数，说是适当是避免出现未定式的情况，也就是负无穷+正无穷
（2）仿射映射的复合，若$f$为闭函数，则$f(Ax+b)$也为闭函数
（3）取上确界，若每一个函数$f_{\alpha }$均为闭函数，则$su{p}_{\alpha }{f}_{\alpha }(x)$也为闭函数。