版本说明

当前版本号[20230807]。

版本	修改说明
20230807	初版

文章目录

版本说明
977.有序数组的平方
- 思路
- - 暴力排序
  - 双指针法
- 两种方法的区别
总结

977.有序数组的平方

力扣题目链接
更多内容可点击此处跳转到代码随想录，看原版文件

给你一个按非递减顺序排序的整数数组 nums，返回每个数字的平方组成的新数组，要求也按非递减顺序排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]，排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

思路

暴力排序

最直观的想法，莫过于：每个数平方之后，排个序，美滋滋，代码如下：

class Solution {
    public int[] sortedSquares(int[] A) {
        for (int i = 0; i < A.length; i++) {
            A[i] *= A[i];
        }
        Arrays.sort(A);
        return A;
    }
}

这个时间复杂度是 O(n + nlogn)，可以说是O(nlogn)的时间复杂度，但为了和下面双指针法算法时间复杂度有鲜明对比，我记为 O(n + nlog n)。

双指针法

数组其实是有序的，只不过负数平方之后可能成为最大数了。

那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。

此时可以考虑双指针法了，i指向起始位置，j指向终止位置。

定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。

如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。

如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。

如下展示：

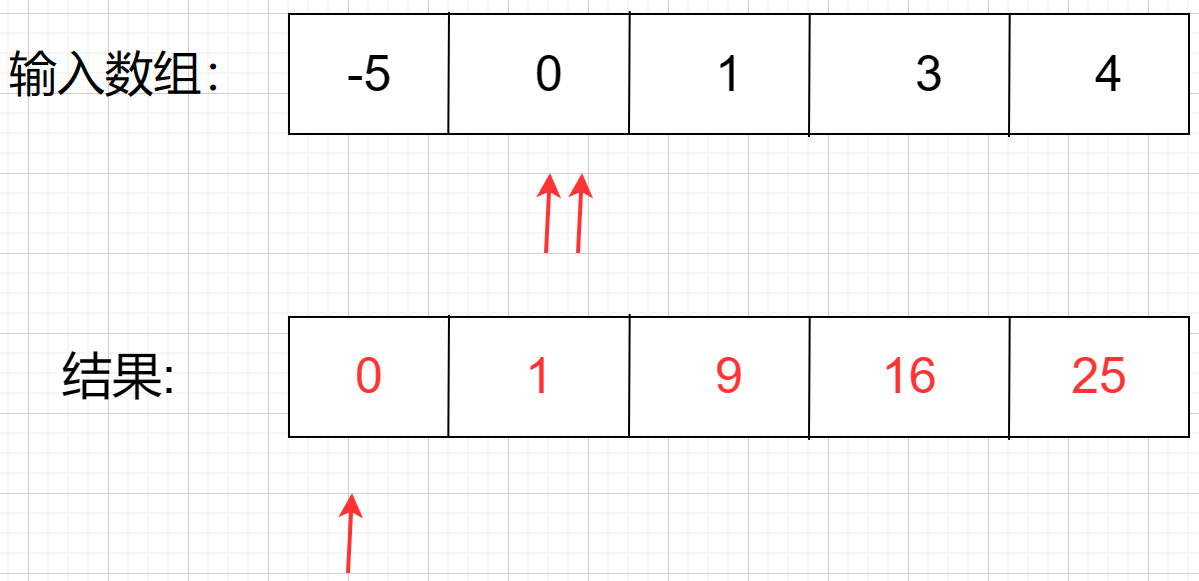
第一步，新建数组【前提：所输入的是非递减数列】

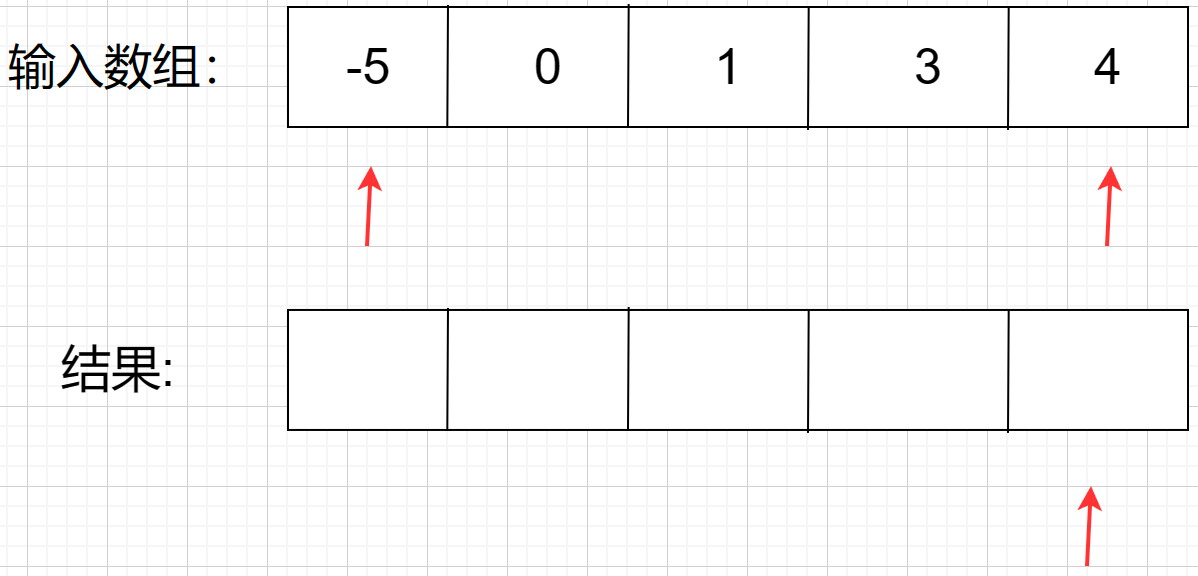
第二步：左、右指针比较平方大小，发现左指针的数值大，于是把 25 放进结果里，同时结果的下标往左走，左指针往右走

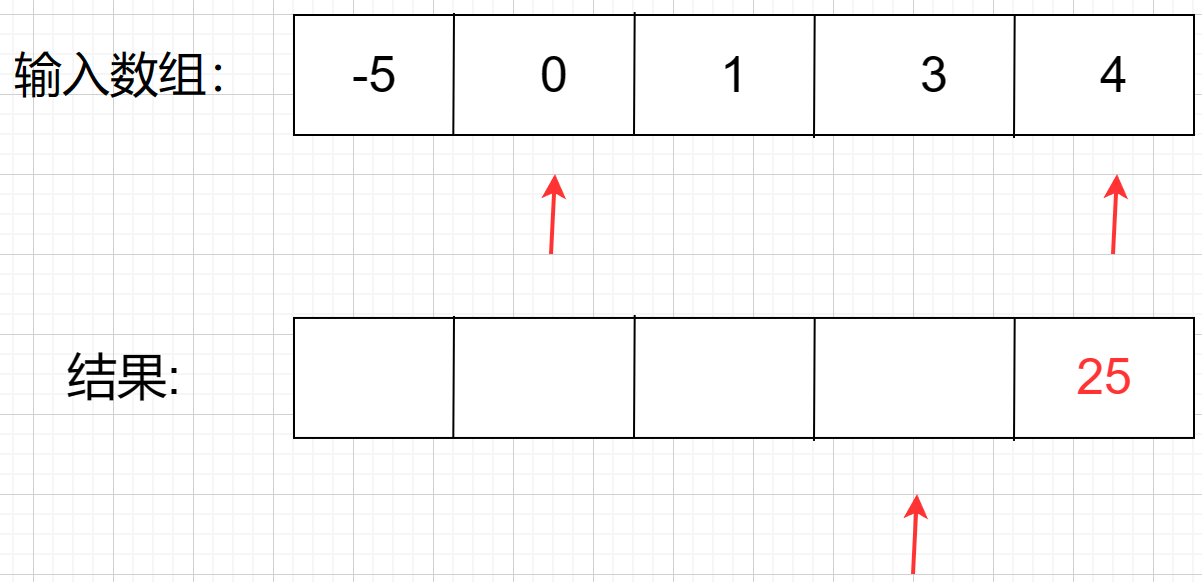
第三步，继续往下走，发现右指针的数值大，于是把 16 放进结果里，同时结果的下标往左走，右指针往左走

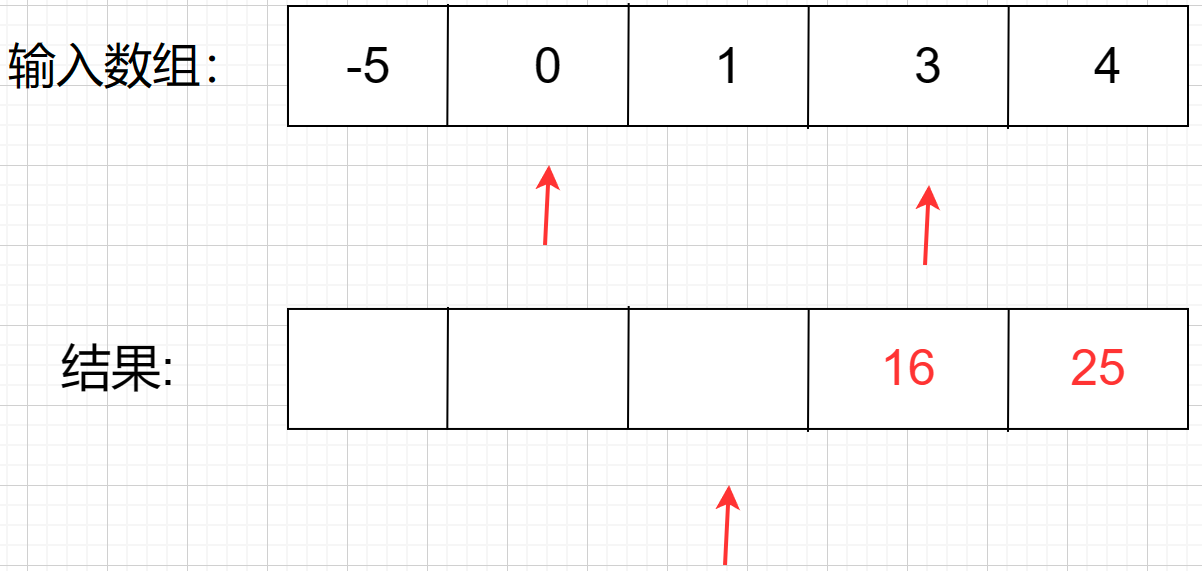
最后一步，结果就出来了

示例代码：

class Solution {
    public int[] sortedSquares(int[] nums) {
        int l = 0;
        int r = nums.length - 1;//定义两个指针left(l)和right(r)，分别指向数组的开头和结尾。
        int[] res = new int[nums.length];//定义一个新的数组result(res)，用于存储平方后的结果。
        int j = nums.length - 1;//指向数组的结尾
        while(l <= r){
            if(nums[l] * nums[l] > nums[r] * nums[r]){
                res[j--] = nums[l] * nums[l++];
            }else{
                res[j--] = nums[r] * nums[r--];
            }
        }
    //使用一个循环，当left小于等于right时，执行以下步骤：
    //比较left指向的元素的平方和right指向的元素的平方的大小。
    //如果left指向的元素的平方较大，将其放入结果数组result的末尾，并将left指针向右移动一位。
    //如果right指向的元素的平方较大或两者相等，将其放入结果数组result的末尾，并将right指针向左移动一位。
        return res;//返回结果数组result(res)
    }
}

此时的时间复杂度为O(n)，相对于暴力排序的解法O(n + nlog n)还是提升不少的。

两种方法的区别

解决给定问题的暴力解法中，我们可以使用以下步骤：

遍历输入数组nums中的每个元素。
对每个元素进行平方操作，并将平方值放入一个新的数组中。
对新数组进行排序。
返回排序后的新数组。

这种方法的时间复杂度为O(nlogn)，其中n是输入数组的长度。原因是我们使用了一个内置的排序算法对新数组进行排序。

而在使用双指针的方法中，我们利用输入数组已经按非递减顺序排序的特点，通过双指针从两端向中间移动的方式来解决问题。具体步骤如下：

定义两个指针left和right，分别指向输入数组nums的开头和结尾。
定义一个新的数组result，用于存储平方后的结果。
使用一个index指针，从结果数组result的末尾开始填充元素。
使用一个循环，当left小于等于right时，执行以下步骤：
- 比较left指向的元素的平方和right指向的元素的平方的大小。
- 如果left指向的元素的平方较大，将其放入结果数组result的末尾，并将left指针向右移动一位。
- 如果right指向的元素的平方较大或两者相等，将其放入结果数组result的末尾，并将right指针向左移动一位。
- 将index指针向前移动一位。
返回结果数组result。

这种方法的时间复杂度为O(n)，其中n是输入数组的长度。因为我们只需要遍历一次输入数组，并利用双指针从两端向中间移动的方式。

因此，使用双指针法可以在线性时间复杂度下解决该问题，而暴力解法则需要使用排序算法，时间复杂度较高。所以，双指针法是更高效的解决方案。

总结

对于这个问题，我们可以使用双指针的方法来解决。由于输入的数组已经是按非递减顺序排序的，**我们可以使用两个指针分别指向数组的开头和结尾，比较两个指针指向的元素的平方大小，然后将较大的平方值放入结果数组的末尾，并将相应的指针向中间移动。**重复这个过程直到两个指针相遇。

通过比较每个元素的平方值的大小，将较大的值放入结果数组，并不断向中间移动指针，最终得到按非递减顺序排序的每个数字的平方组成的新数组。

我们也可以写一个测试方法，输入一个非递减顺序排序的数组，来验证代码的正确性。

测试代码：

package shuzhu;

public class Day03
{
    public static int[] sortedSquares(int[] nums) {
        int l = 0;
        int r =nums.length - 1;
        int[] res = new int[nums.length];
        int j = nums.length - 1;
        while(l <= r)
        {
            if(nums[l] * nums[l] >nums[r] * nums[r])
            {
                res[j] = nums[l] * nums[l];
                j--;
                l++;
            }
            else
            {
                res[j] = nums[r] * nums[r];
                j--;
                r--;
            }
        }
        return res;
    }

    public static void main(String[] args) {
        int[] nums ={-7, 2, 4, 5, 6};
        int[] res = sortedSquares(nums);
        for(int i = 0; i < res.length;i++)
        {
            System.out.print(res[i]+" ");
        }
    }
}

        int[] nums ={-7, 2, 4, 5, 6};
        int[] res = sortedSquares(nums);
        for(int i = 0; i < res.length;i++)
        {
            System.out.print(res[i]+" ");
        }
    }
}