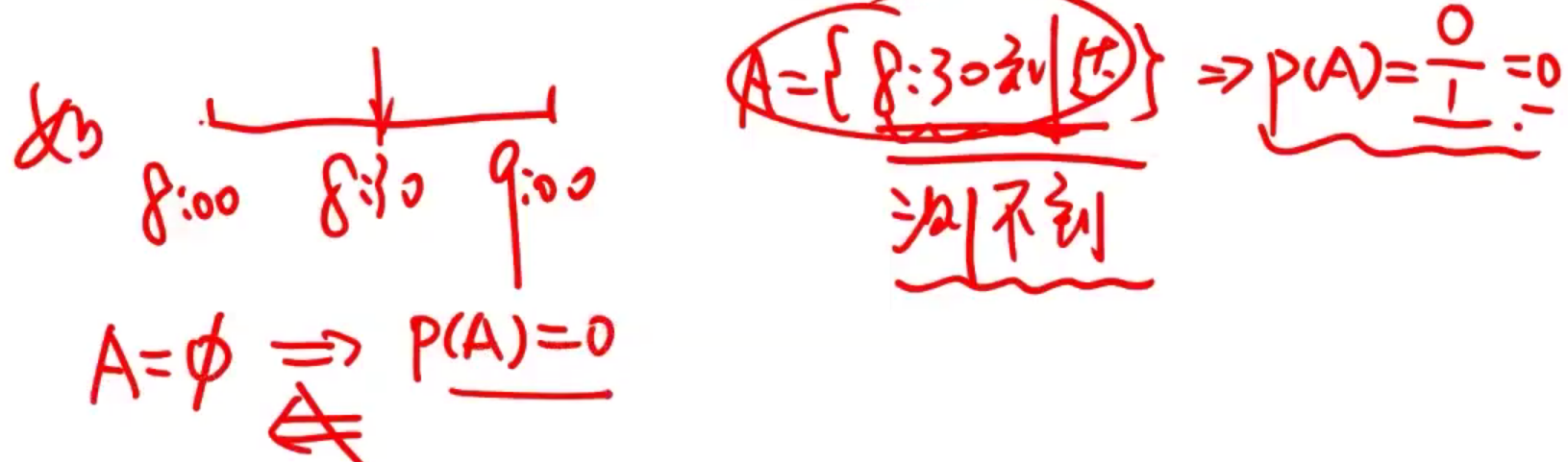文章目录
- 概率论
- Ch1. 随机事件及其概率
- 1.基本概念
- (1)随机试验、随机事件、样本空间
- (2)事件的关系和运算
- ①定义:互斥(互不相容)、对立
- ②运算法则:德摩根率
- (3)概率的定义
- (4)概率的性质
- (5)概率计算
- 排列组合
- 2.等可能概型
- 1.古典概型 (离散)
- 2.几何概型 (连续)
- 3.七大公式
- (1)逆事件概率公式
- (2)加法公式
- (3)减法公式
- (4)条件概率公式
- (5)乘法公式
- (6)全概率公式
- (7)贝叶斯公式 (先验概率)
- 4.独立性
- (1)事件的独立性
- (2)n重伯努利概型 (独立试验序列概型)
概率论


Ch1. 随机事件及其概率
1.基本概念
①古典概型求概率
②几何概型求概率
③七大公式求概率
④独立性
(1)随机试验、随机事件、样本空间
1.随机试验 E

2.随机事件 A、B、C
①必然事件 Ω:
P
(
Ω
)
=
1
P(Ω)=1
P(Ω)=1
②不可能事件 Ø:
P
(
Ø
)
=
0
P(Ø)=0
P(Ø)=0

3.样本空间
①样本点 ω = 基本事件
②样本空间 Ω:样本点的全体组成的集合

(2)事件的关系和运算
①定义:互斥(互不相容)、对立
(一) 关系:包含、相等、相容、(互不相容)互斥、对立
(二) 运算:和(并)、差、积(交)
(一) 事件的关系
1.包含
(1)概念:

(2)性质:
①
A
⊂
B
A \subset B
A⊂B,则
P
(
A
)
≤
P
(
B
)
P(A)≤P(B)
P(A)≤P(B)
②
A
B
⊂
A
AB\subset A
AB⊂A且
A
B
⊂
B
AB\subset B
AB⊂B,即 P(AB)≤P(A)且P(AB)≤P(B)
(3)若事件C发生必然导致事件A与B同时发生,则A、B、C事件关系为: C ⊂ A B C\subset AB C⊂AB
2.相等

3.相容

4.互不相容(互斥)
(1)定义:
若事件A,B互斥,则
①事件角度:AB=Ø
②概率角度:P(AB)=0
(2)性质:
AB=Ø,则
A
⊂
B
‾
A\subset \overline B
A⊂B,
P
(
A
)
≤
P
(
B
‾
)
P(A)≤P(\overline B)
P(A)≤P(B)

5.对立:对立事件、逆事件
①
A
B
=
Ø
AB=Ø
AB=Ø 且
A
∪
B
=
Ω
A∪B=Ω
A∪B=Ω (即
A
ˉ
\bar{A}
Aˉ=B)
②P(AB)=0 且 P(A)+P(B)=1

(二)事件的运算
1.和(并):A∪B
2.差:$A-B=A∩\overline{B} $

3.积(交):A∩B 或 AB
例题1:12年14.
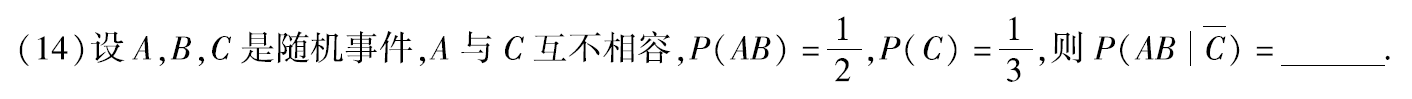
答案:3/4
②运算法则:德摩根率
5.德摩根率(对偶律) 【长杠变短杠,开口换方向】
(1)
A
∪
B
‾
=
A
‾
∩
B
‾
=
A
‾
B
‾
\overline{A∪B}=\overline{A}∩\overline{B}=\overline{A}\ \overline{B}
A∪B=A∩B=A B:A、B均不发生
(2)
A
B
‾
=
A
‾
∪
B
‾
\overline{AB}=\overline{A}∪\overline{B}
AB=A∪B:A、B至少有一个不发生
方法:转化为带并的来看含义
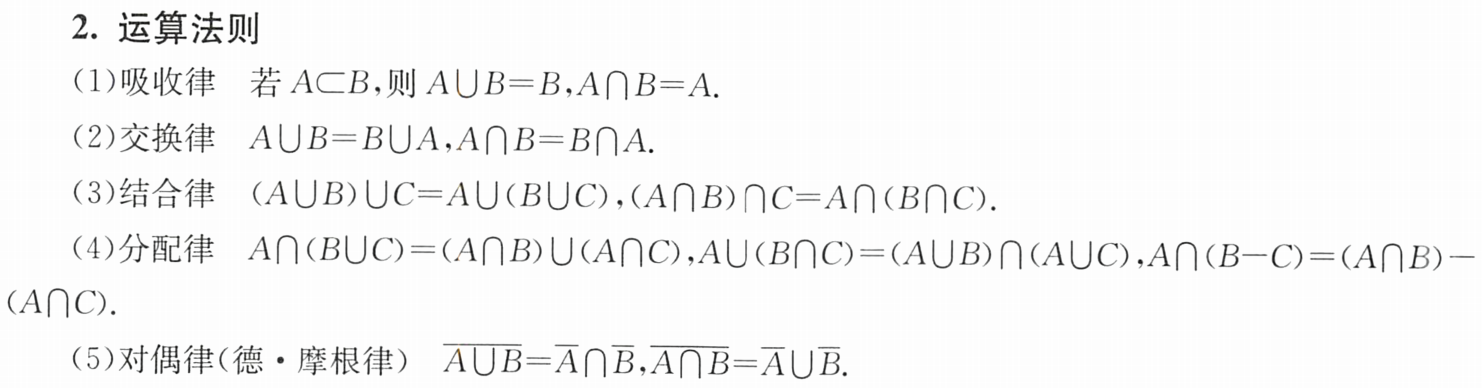
例题1:

分析:
A={甲畅销,乙滞销}=B∩C
A
ˉ
=
B
∩
C
‾
=
B
‾
∪
C
‾
\bar{A}=\overline{B∩C}=\overline{B}∪\overline{C}
Aˉ=B∩C=B∪C=甲滞销 或 乙畅销
答案:C
例题2:

法一:推导
法二:画图
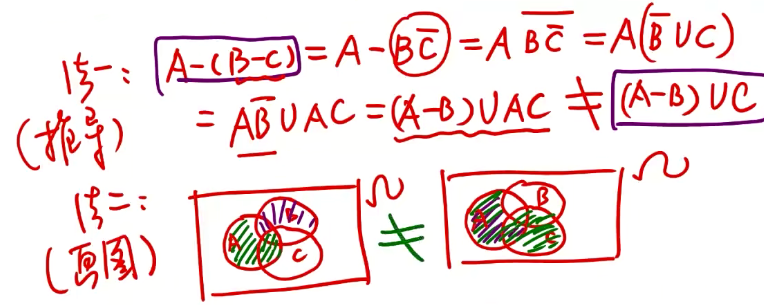
(3)概率的定义
1.用频率去估计概率

2.概率的公理化定义
①非负性:
P
(
A
)
≥
0
P(A)≥0
P(A)≥0
②规范性:
P
(
Ω
)
=
1
P(Ω)=1
P(Ω)=1
③可列可加性:任意可列个两两互不相容的事件
A
1
,
A
2
,
.
.
.
,
A
n
A_1,A_2,...,A_n
A1,A2,...,An,有
P
(
A
1
∪
A
2
∪
.
.
.
∪
A
n
)
=
P
(
A
1
)
+
P
(
A
2
)
+
.
.
.
+
P
(
A
n
)
P(A_1∪A_2∪...∪A_n)=P(A_1)+P(A_2)+...+P(A_n)
P(A1∪A2∪...∪An)=P(A1)+P(A2)+...+P(An) 【完备事件组】
(4)概率的性质
(1)有界性:
对任意事件A,有
0
≤
P
(
A
)
≤
1
0≤P(A)≤1
0≤P(A)≤1。
注:对于几何概型:若P(A)=0,不能断言 A=Ø;若P(A)=1,不能断言 A=Ω;
但反之则对:若A是空集Ø,则P(A)=0;若A是全集Ω,则P(A)=1。即一定有 P ( Ø ) = 0 , P ( Ω ) = 1 P(Ø)=0,P(Ω)=1 P(Ø)=0,P(Ω)=1。
(2)单调性:
对于A,B两个事件,若有
A
⊂
B
A\subset B
A⊂B,则有:
①P(A)≤P(B)
②P(B-A)=P(B)-P(A)
(5)概率计算
跳转链接
排列组合
| 排列 | 组合 | |
|---|---|---|
| 符号 | A n m A_n^m Anm | C n m C_n^m Cnm |
| 公式 | A n m = n ( n − 1 ) . . . ( n − m − 1 ) A_n^m=n(n-1)...(n-m-1) Anm=n(n−1)...(n−m−1) | C n m = n ( n − 1 ) . . . ( n − m − 1 ) m ! C_n^m=\dfrac{n(n-1)...(n-m-1)}{m!} Cnm=m!n(n−1)...(n−m−1) |
| 关系 | A n m = A_n^m= Anm= | C n m ⋅ m ! C_n^m·m! Cnm⋅m! |
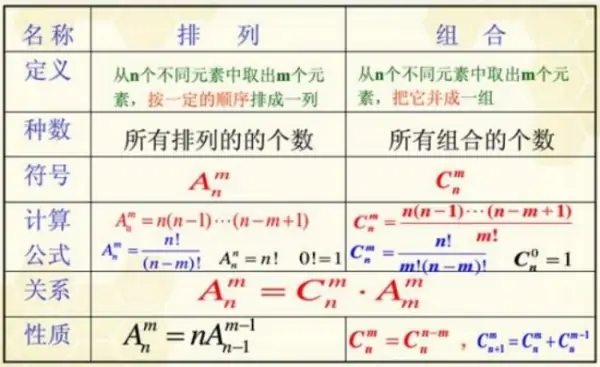
2.等可能概型
1.古典概型 (离散)
古典概型(离散),研究工具:①排列组合 ②加法原理、乘法原理 ③直接数数

求法:
(1)直接用定义求概率:
P
(
A
)
=
k
n
P(A)=\dfrac{k}{n}
P(A)=nk
(2)随机分配:m个可辩质点,放到n个盒子中
①每个盒子可以放任意多个质点:有
n
m
n^m
nm 种放法
②每个盒子只能放一个质点:有
A
n
m
=
n
(
n
−
1
)
.
.
.
(
n
−
m
+
1
)
A_n^m=n(n-1)...(n-m+1)
Anm=n(n−1)...(n−m+1) 种放法

(3)简单随机抽样
| 含义 | 共有多少种不同的取法 | |
|---|---|---|
| ①先后有放回 | m个球,先后有放回地取n次 | m n m^n mn |
| ②先后无放回 | m个球,先后无放回地取n次 | A m n = m ( m − 1 ) . . . ( m − n + 1 ) A_m^n=m(m-1)...(m-n+1) Amn=m(m−1)...(m−n+1) |
| ③任取(一次性同时拿出) | 从n中一次性取m个球 | C n m C_n^m Cnm |

2.几何概型 (连续)
几何概型(连续),研究工具:几何方法、微积分
P ( A ) = S A 的几何度量 Ω 的几何度量 P(A)=\dfrac{S_A的几何度量}{Ω的几何度量} P(A)=Ω的几何度量SA的几何度量
几何度量:长度、面积、体积

例题1:07年16. 几何概型

分析:
法一:直接观察,使得 x-y绝对值小于0.5

显然,概率应为
3
4
\dfrac{3}{4}
43
法二:随机变量的概率
| 文字语言 | 数学语言 |
|---|---|
| 两个数之差的绝对值 | ∣ X − Y ∣ \lvert X-Y\rvert ∣X−Y∣ |
| 两个数之差的绝对值小于 1 2 \dfrac{1}{2} 21 | ∣ X − Y ∣ < 1 2 \lvert X-Y\rvert<\dfrac{1}{2} ∣X−Y∣<21 |
| 两个数之差的绝对值小于 1 2 \dfrac{1}{2} 21的概率 | P { ∣ X − Y ∣ < 1 2 } P\{\ \lvert X-Y\rvert<\dfrac{1}{2}\ \} P{ ∣X−Y∣<21 } |
则 P { ∣ X − Y ∣ < 1 2 } = P { − 1 2 < X − Y < 1 2 } = P { − 1 2 < Y − X < 1 2 } = P { x − 1 2 < Y < x + 1 2 } P\{|X-Y|<\dfrac{1}{2}\}=P\{-\dfrac{1}{2}<X-Y<\dfrac{1}{2}\}=P\{-\dfrac{1}{2}<Y-X<\dfrac{1}{2}\}=P\{x-\dfrac{1}{2}<Y<x+\dfrac{1}{2}\} P{∣X−Y∣<21}=P{−21<X−Y<21}=P{−21<Y−X<21}=P{x−21<Y<x+21}
即在 0 < x < 1 , 0 < y < 1 0<x<1,0<y<1 0<x<1,0<y<1区域内,落在 y = x + 1 2 y=x+\dfrac{1}{2} y=x+21 和 y = x − 1 2 y=x-\dfrac{1}{2} y=x−21 之间的概率。

答案: 3 4 \dfrac{3}{4} 43
3.七大公式
(1)逆事件概率公式
P ( A ‾ ) = 1 − P ( A ) P(\overline A)=1-P(A) P(A)=1−P(A)
(2)加法公式
1.任意事件
①两事件和的概率:
P
(
A
∪
B
)
=
P
(
A
)
+
P
(
B
)
−
P
(
A
B
)
P(A∪B)=P(A)+P(B)-P(AB)
P(A∪B)=P(A)+P(B)−P(AB)
②三事件和的概率:
P
(
A
∪
B
∪
C
)
=
P
(
A
)
+
P
(
B
)
+
P
(
C
)
−
P
(
A
B
)
−
P
(
B
C
)
−
P
(
A
C
)
+
P
(
A
B
C
)
P(A∪B∪C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC)
P(A∪B∪C)=P(A)+P(B)+P(C)−P(AB)−P(BC)−P(AC)+P(ABC)
③四事件和的概率:
P
(
A
∪
B
∪
C
∪
D
)
=
[
P
(
A
)
+
P
(
B
)
+
P
(
C
)
+
P
(
D
)
]
−
[
P
(
A
B
)
+
P
(
A
C
)
+
P
(
A
D
)
+
P
(
B
C
)
+
P
(
B
D
)
+
P
(
C
D
)
]
+
[
P
(
A
B
C
)
+
P
(
A
B
D
)
+
P
(
A
C
D
)
+
P
(
B
C
D
)
]
−
P
(
A
B
C
D
)
P(A∪B∪C∪D)=[P(A)+P(B)+P(C)+P(D)]-[P(AB)+P(AC)+P(AD)+P(BC)+P(BD)+P(CD)]+[P(ABC)+P(ABD)+P(ACD)+P(BCD)]-P(ABCD)
P(A∪B∪C∪D)=[P(A)+P(B)+P(C)+P(D)]−[P(AB)+P(AC)+P(AD)+P(BC)+P(BD)+P(CD)]+[P(ABC)+P(ABD)+P(ACD)+P(BCD)]−P(ABCD)
2.两两互不相容事件:
互斥条件下的加法公式,和的概率 = 概率的和

(3)减法公式
P ( A − B ) = P ( A ) − P ( A B ) = P ( A B ‾ ) P(A-B)=P(A)-P(AB)=P(A\overline{B}) P(A−B)=P(A)−P(AB)=P(AB)

(4)条件概率公式
条件概率:A发生条件下,B发生的概率,记为 P ( B ∣ A ) P(B|A) P(B∣A),前提要求P(A)>0 【垂帘听政】
P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\dfrac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB)
注:①条件概率也是概率,概率的性质仍都满足
(5)乘法公式
① P ( A B ) = P ( A ) ⋅ P ( B ∣ A ) P(AB)=P(A)·P(B|A) P(AB)=P(A)⋅P(B∣A)
② P ( A 1 A 2 A 3 ) = P ( A 1 ) P ( A 2 ∣ A 1 ) P ( A 3 ∣ A 1 A 2 ) P(A_1A_2A_3)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2) P(A1A2A3)=P(A1)P(A2∣A1)P(A3∣A1A2) 【上过台的,到帘子后面】
(6)全概率公式
1.完备事件组:任意两两互斥,概率有可列可加性
2.全概率公式 【全集分解公式,由因导果】
P
(
B
)
=
∑
i
=
1
n
P
(
B
A
i
)
=
P
(
B
A
1
)
+
P
(
B
A
2
)
+
.
.
.
P
(
B
A
n
)
=
P
(
A
1
)
P
(
B
∣
A
1
)
+
P
(
A
2
)
P
(
B
∣
A
2
)
+
.
.
.
+
P
(
A
n
)
P
(
B
∣
A
n
)
P(B) = \sum\limits_{i=1}^nP(BA_i)=P(BA_1)+P(BA_2)+...P(BA_n)=P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+...+P(A_n)P(B|A_n)
P(B)=i=1∑nP(BAi)=P(BA1)+P(BA2)+...P(BAn)=P(A1)P(B∣A1)+P(A2)P(B∣A2)+...+P(An)P(B∣An) 【谁去干的概率×干成功的概率】
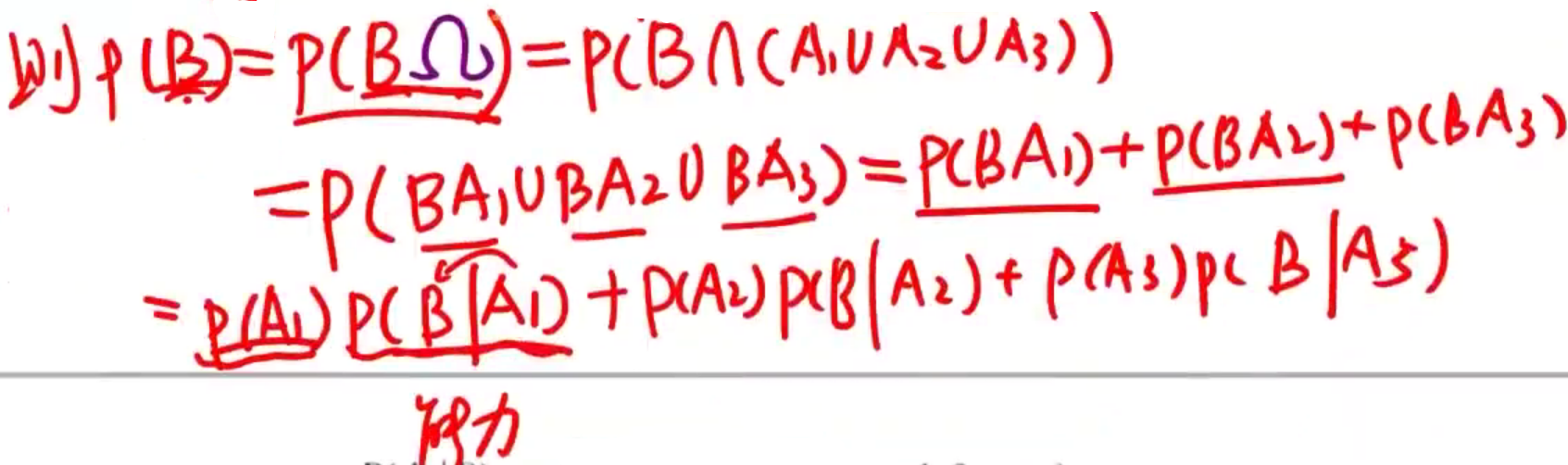
例: P { Y ≤ y } = P { X = 1 } ⋅ P { Y ≤ y ∣ X = 1 } + P { X = 2 } ⋅ P { Y ≤ y ∣ X = 2 } P\{Y≤y\} = P\{X=1\}·P\{Y≤y|X=1\}+ P\{X=2\}·P\{Y≤y|X=2\} P{Y≤y}=P{X=1}⋅P{Y≤y∣X=1}+P{X=2}⋅P{Y≤y∣X=2}
对y的取值进行分类讨论:①y<0 ②0≤y<1 ③1≤y<2 ④y>2
(7)贝叶斯公式 (先验概率)
贝叶斯公式(逆概率公式,执果索因):已知B发生了,求是谁干的?
P ( A k ∣ B ) = P ( B A k ) P ( B ) = P ( A k ) P ( B ∣ A k ) ∑ i = 1 n P ( A i ) P ( B ∣ A i ) = 全概率的某一项 全概率公式 P(A_k|B)=\dfrac{P(BA_k)}{P(B)}=\dfrac{P(A_k)P(B|A_k)}{\sum\limits_{i=1}^nP(A_i)P(B|A_i)}=\dfrac{全概率的某一项}{全概率公式} P(Ak∣B)=P(B)P(BAk)=i=1∑nP(Ai)P(B∣Ai)P(Ak)P(B∣Ak)=全概率公式全概率的某一项
在全概率时,每个人干的可能性一般是等可能的。但当事件发生后,每个人干的可能性就发生了变化。
即贝叶斯公式:增加信息,概率的大小可能要修正
例题1:随机事件的概率

分析: 德摩根律(对偶率)
A
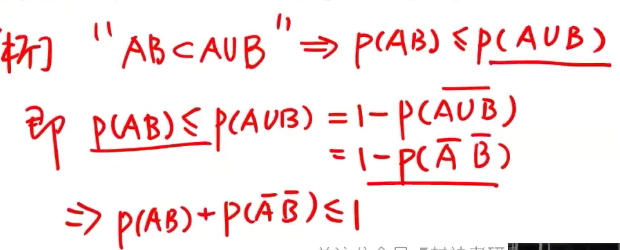
C 包含的性质
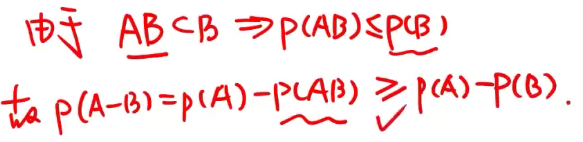
D 逆事件概率公式 + 德摩根律(对偶率)
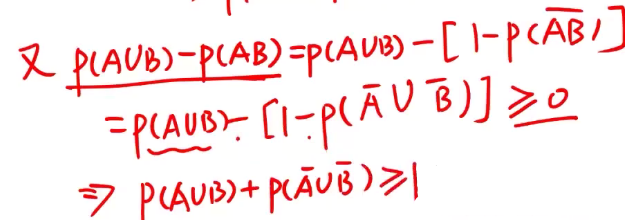
答案:A
例题2:18年14. 条件概率、事件的独立性
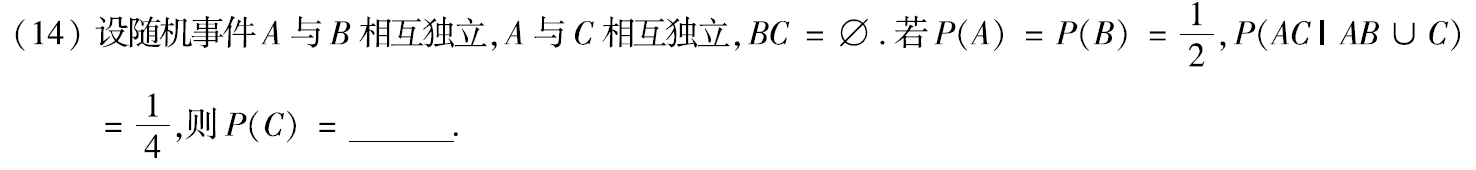
分析:关键是分析出P(AC(AB∪C))=P(AC)
因为BC=Ø,∴P(BC)=0,P(ABC)=0
P
(
A
C
∣
A
B
∪
C
)
=
P
(
A
C
(
A
B
∪
C
)
)
P
(
A
B
∪
C
)
=
P
(
A
B
C
∪
A
C
)
)
P
(
A
B
∪
C
)
=
P
(
A
C
)
)
P
(
A
B
)
+
P
(
C
)
−
P
(
A
B
C
)
=
P
(
A
)
P
(
C
)
)
P
(
A
)
P
(
B
)
+
P
(
C
)
=
1
4
P(AC|AB∪C)=\dfrac{P(AC(AB∪C))}{P(AB∪C)}=\dfrac{P(ABC∪AC))}{P(AB∪C)}=\dfrac{P(AC))}{P(AB)+P(C)-P(ABC)}=\dfrac{P(A)P(C))}{P(A)P(B)+P(C)}=\dfrac{1}{4}
P(AC∣AB∪C)=P(AB∪C)P(AC(AB∪C))=P(AB∪C)P(ABC∪AC))=P(AB)+P(C)−P(ABC)P(AC))=P(A)P(B)+P(C)P(A)P(C))=41
∴
P
(
C
)
=
1
4
∴P(C)=\dfrac{1}{4}
∴P(C)=41

答案:
1
4
\dfrac{1}{4}
41
例题3:15年7. 交与并、加法公式

分析:交的概率大于等于并的概率
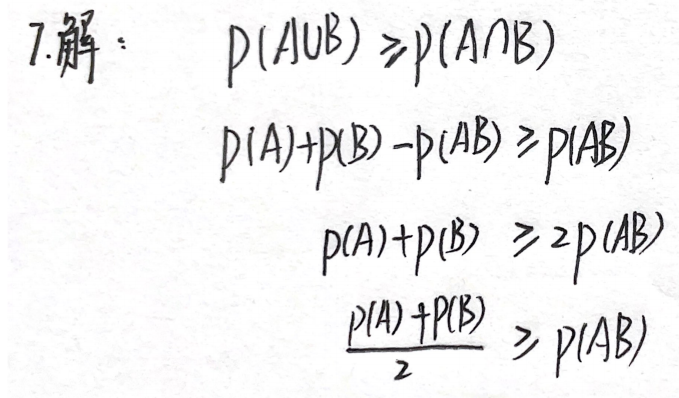
答案:C
例题4:21年16. 全概率公式 + 条件概率

分析:

答案: 1 5 \dfrac{1}{5} 51
例题5:23李林六(三)16.
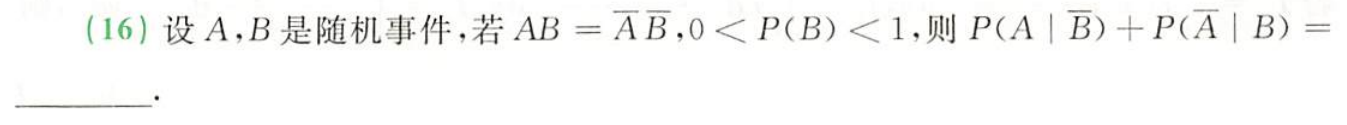
分析:法1:特殊值 法2:正面解

答案:2
例题6:全概率公式

分析:分两次全概率:①抽验样本为正品 ②该箱通过验收

答案:0.887
例题7:贝叶斯公式

分析:

答案: 3 28 \dfrac{3}{28} 283
4.独立性
(1)事件的独立性
(1)数学定义:事件A、B独立 ⇔ P ( A B ) = P ( A ) ⋅ P ( B ) \Leftrightarrow P(AB)=P(A)·P(B) ⇔P(AB)=P(A)⋅P(B)
不可能事件Ø,与任意事件独立
(2)可推得A、B独立条件下的条件概率公式: P ( A ∣ B ) = P ( A ) , P ( B ∣ A ) = P ( B ) P(A|B)=P(A),P(B|A)=P(B) P(A∣B)=P(A),P(B∣A)=P(B) 【描述性定义:结果不受影响 】

(3)n个事件相互独立、n个事件两两独立

例题1:
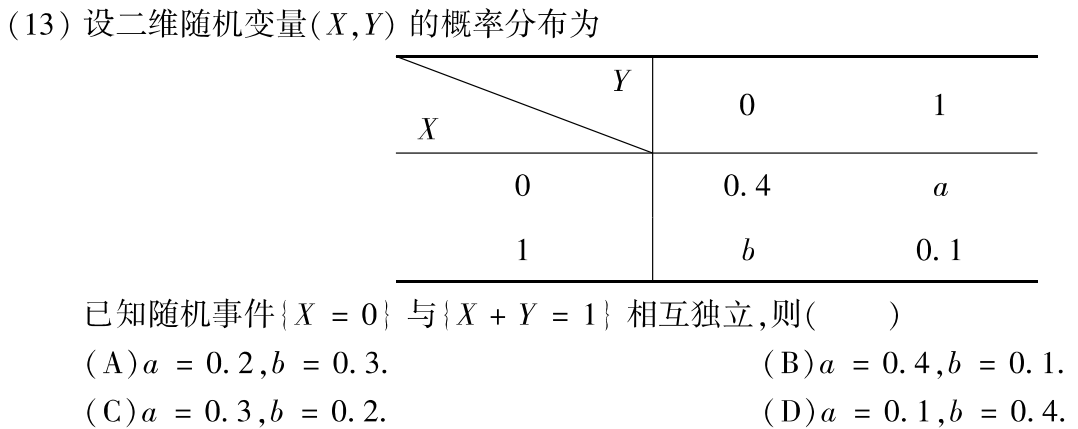
分析:

答案:B
(2)n重伯努利概型 (独立试验序列概型)
n重伯努利试验