背景
Transformer已经在NLP领域大展拳脚,逐步替代了LSTM/GRU等相关的Recurrent Neural Networks,相比于传统的RNN,Transformer主要具有以下几点优势
- 可解决长时序依赖问题,因为Transformer在计算attention的时候是在全局维度进行展开计算的,所以不存在长时序中的梯度消失等问题。
- Transformer的encoder和decoder在某些场景下均可以很好的并行化,提高的计算效率。
- Transformer具备比较好的可解释性
- Transformer的可扩展性比较强,可以灵活的增加层数。
在视觉领域也有一些方法逐步的在引入Transformer来解决一些视觉挑战任务,例如基于图片分类的ViT。本文是将Transformer引入目标检测领域中来,可以端到端的解决目标检测的问题,相比于传统基于anchor/proposal/NMS的方法而言,本文的方法主要有以下优势:
- 摆脱了对原有的基于先验知识的依赖,不再依赖proposal/NMS等基于先验的方法,整个网络是完全learnable的,并且简化了整体的pipeline。
- 相比于NMS,可以在全局视角考虑整体的最优性,消除整体的冗余。
方法
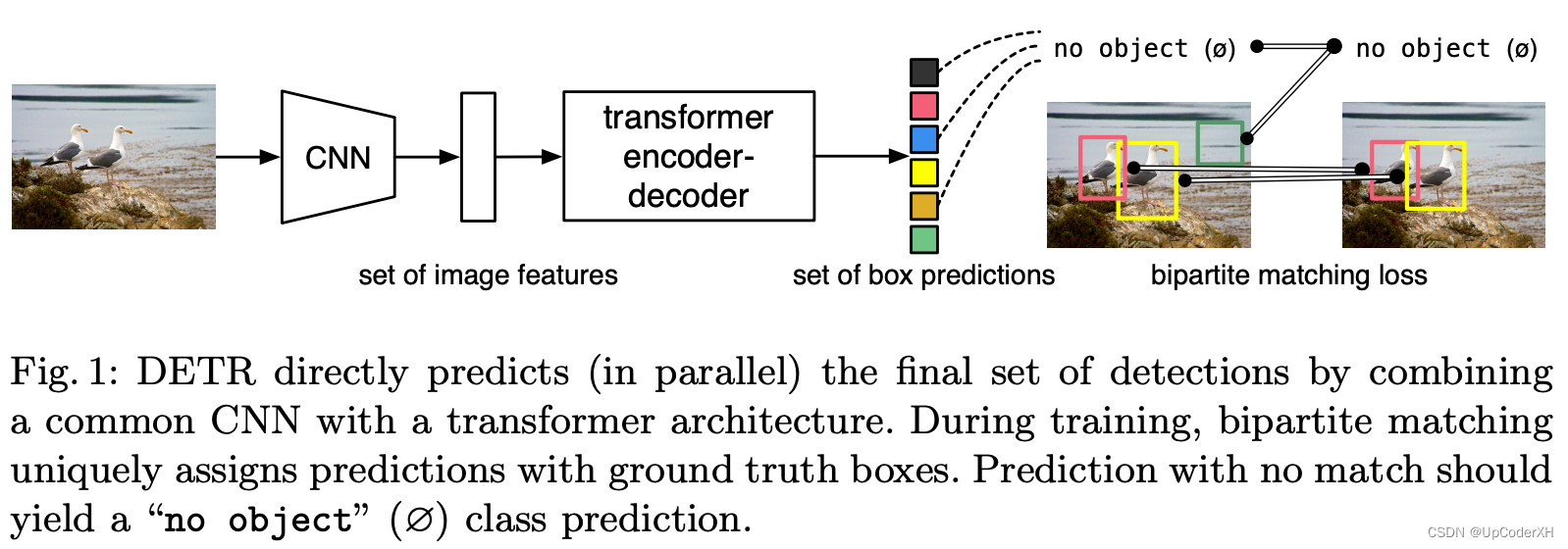
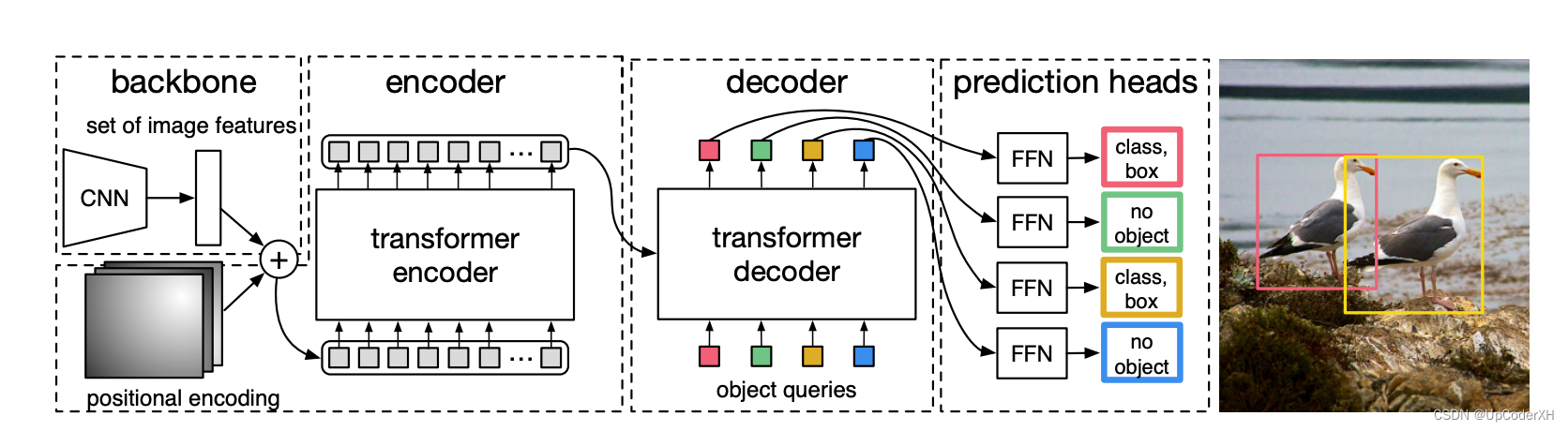
本文提出的网络结构整体上如下图所示。接下来我们将从网络结构、损失函数和匹配方法分别展开介绍
网络结构
整体的网络结构如上图所示,一张图片我们通过CNN抽取其基本的视觉特征(待讨论能不能像ViT那样,做到完全的Transformer)。得到feature map
F
∈
R
H
×
W
×
C
F \in R^{H \times W \times C}
F∈RH×W×C,然后我们将其reshape成为
F
∈
R
(
H
×
W
)
×
C
F \in R^{(H \times W) \times C}
F∈R(H×W)×C。那么我们就得到一个长度为
H
×
W
H \times W
H×W的序列,每个unit的维度的是
C
C
C。
我们再将得到的序列输入到transformer的encoder进行特征的加工,相当于重构每个unite的表征,使其可以从全局的视角加载特征和。这里的unit相当于就是“Proposal”。
Encoder输出后的feature再会输入给decoder,decoder基于Encoder的特征和位置编码特征输出每个位置应该预测的proposal。如下图所示,object queries就是每个position的embedding。
-
QA1:Encoder和Decoder的position embedding是不是一样的?
- 答案是不一样的,Encoder的position embedding可以理解是二维的,他针对feature map上的每一个位置进行embedding。而Decoder中的position embedding是“proposal”维度的,先验是一张图片最多会有100个框,所以Decoder中最多会有100个position。Decoder的position embedding是lookup 查表得到的,整体上第一个position代表什么含义?是否有说明?
- 具体实现上,object queries是 N(100) 个learnable embedding,训练刚开始时可以随机初始化。在训练过程中,因为需要生成不同的boxes,object queries会被迫使变得不同来反映位置信息,所以也可以称为leant positional encoding (注意和encoder中讲的position encoding区分,不是一个东西)。
- 由于在训练过程中,会预测100个框,然后和gt去做匹配,计算loss,这就会反推每个decoder的position embedding默认代表某个位置的框?但是实验代码并没有可视化说明?
-
QA2:Decoder中的QKV分别是什么?
Encoder不用说,就是unit的特征。Decoder中- Q:查询的信息,一般就是position embedding,由于这里会引入先验,最多100个框,所以Q的size为 R 100 × d R^{100 \times d} R100×d
- K:和基础的transformer一样,第一层的attention K和V都是上面的Q。第二层的attention K为Encoder的输入,一般大小为 R ( H × W ) × d R^{(H \times W) \times d} R(H×W)×d
- V:和基础的transformer一样,第一层的attention K和V都是上面的Q。第二层的attention K为Encoder的输入,一般大小为
R
(
H
×
W
)
×
d
R^{(H \times W) \times d}
R(H×W)×d
损失函数
损失函数整体由三部分组成,分类损失+l1loss+GIoU loss。后面两个算是位置优化的损失函数。为什么需要两个?
- L1的劣势:不具备尺度不变性。大物体和小物体之间的loss是不公平的。
- GIoU的劣势:收敛过慢(DIoU中有说)
- GIoU的定义
L g i o u = I o U − C − u i o n C L_{giou} = IoU - \frac{C-uion}{C} Lgiou=IoU−CC−uion - GIoU的特性
- 非负性、三角不等性
- 尺度不变性
- 取值范围[-1, 1],且GIoU <= IoU。
匹配方法
首先将整个问题抽象为匹配问题。给定N个预测的框和M个GT的框。计算min(N, M)个框之间的一个完全匹配。
具体来说,第一步我们根据上述的损失函数定义,计算一个cost矩阵,
c
o
s
t
i
,
j
cost_{i,j}
costi,j代表的含义就是第i个预测框和第j个gt之间的损失函数。我们是希望寻找到一个最佳匹配,使得整体的损失函数是最小的。这里作者采用的是匈牙利算法。详情可以参考wiki。
- QA1:没有被匹配上的预测框是否计算loss。
这部分从代码来看,会计算分类的loss。而不会计算pos的loss。- pos loss
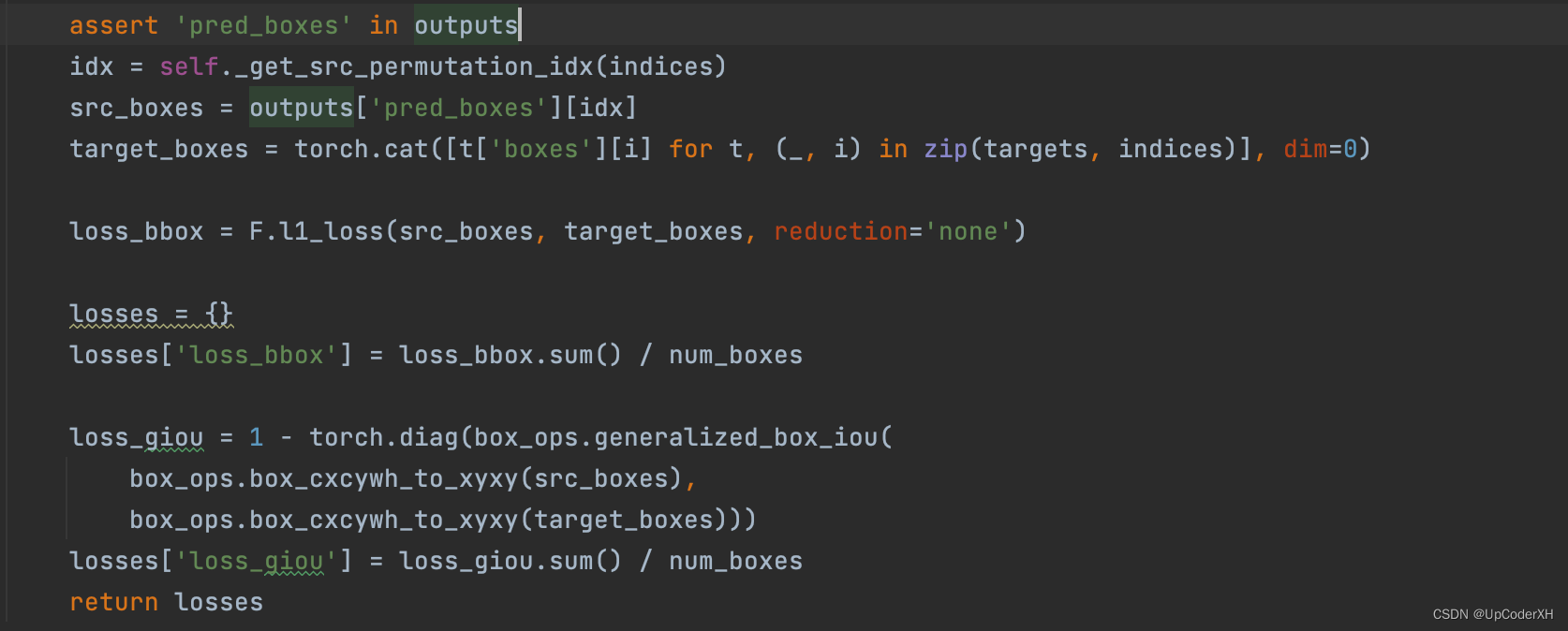
- pos loss
- QA2:匈牙利算法简化版本:
- 给定矩阵C
- 选择每一行中最小的数,并从C中减去,得到C1
- 选择每一列中最小的数,并从C1中减去,得到C2
- 基于C2判断,必须用尽可能少的列或行标记来覆盖矩阵中的所有零。下面的过程是完成这个要求的一种方法:
4.1 首先,尽可能多地分配任务。

4.2 标记所有未分配的行(第 3 行)。
4.3 标记所有新标记的行中 0所在(且未标记)的对应列(第 1 列)。
4.4 标记所有在新标记的列中有分配的行(第 1 行)。
4.5 对所有未分配的行重复上述过程。 - 现在划掉所有已标记的列和未标记的行(第 1 列和第 2, 4 行)。

- 现在删除已画线的行和列。这将留下一个矩阵如下:重新开始步骤2。