一、基本介绍

1.1 线性结构

1.2 非线性顺序结构

二、稀疏数组

2.1 基本介绍

2.1.1 应用场景

2.1.2 实现思路

2.2 代码实现

2.2.1 原始数组

2.2.2 原始数组转化为稀疏数组

2.2.3 稀疏数组转化为原始数组

三、队列的应用场景和介绍

3.1 数组模拟队列

3.1.1数组模拟队列的分析

3.1.2 代码实现数组模拟队列

3.2 环型队列思路分析图

3.2.1 环型队列实现

一、基本介绍

数据结构包括:线性结构和非线性结构。

1.1 线性结构

线性结构作为最常用的数据结构，其特点是数据元素之间存在一对一的线性关系

线性结构有两种不同的存储结构，即顺序存储结构(数组)和链式存储结构(链表)。顺序存储的线性表称为顺序表，顺序表中的存储元素的地址是连续的；链式存储结构中元素的地址不一定连续

链式存储的线性表称为链表，链表中的存储元素不一定是连续的，元素节点中存放数据元素以及相邻元素的地址信息（链表可以充分的利用内存）

线性结构常见的有:数组、队列、链表和栈

1.2 非线性顺序结构

非线性结构包括：二维数组、多维数组、广义表、树结构、图结构（这两种引伸出来了很多算法）

二、稀疏数组

2.1 基本介绍

当一个数组中大部分元素是0，或者为同一个值的数组时，可以使用稀疏数组来保存该数组

处理方法：

记录数组一共几行几列，有多少个不同的值
把具有不同值的元素的行列及值记录在一个小规模的数组中，从而缩小程序的规模

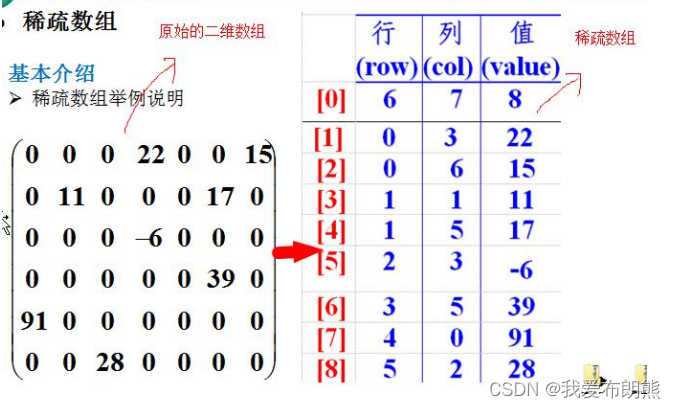
我们看看下面的图，看看稀疏数组到底是怎么回事

如果我们使用左侧的的二维数组直接记录，我们会有6*7=42个数据。

我们看一下右侧的稀疏数组，一打眼就没有42个数据。变成了九行三列 9*3=27个数据

稀疏数组是怎么表示的呢？

表头是行、列、值（利用行、列就可以确定具体的位置，初中的平面坐标系）
第一行记录多少总行数，总列数，有多少个不同的值
下面便开始记录数据，比如第二行，表示第零行（数组是从0开始的，实际是第一行），第三列（左图第四列），此值是22
依次表示出来，只记录非0值的行列值

2.1.1 应用场景

使用稀疏数组，来保留类似前面的二维数组（棋盘、地图等）

把稀疏数组存盘，并且可以从新恢复到原来的二维数组

整体思路分析

2.1.2 实现思路

二维数组转稀疏数组的思路

1. 遍历原始的二维数组，得到有效数据的个数 sum

2. 根据sum 就可以创建稀疏数组 sparseArr int[sum + 1] [3]

3. 将二维数组的有效数据数据存入到稀疏数组

稀疏数组转原始的二维数组的思路

1. 先读取稀疏数组的第一行，根据第一行的数据，创建原始的二维数组，比如上面的 chessArr2 = int [11][11]

2. 在读取稀疏数组后几行的数据，并赋给原始的二维数组即可.

2.2 代码实现

2.2.1 原始数组

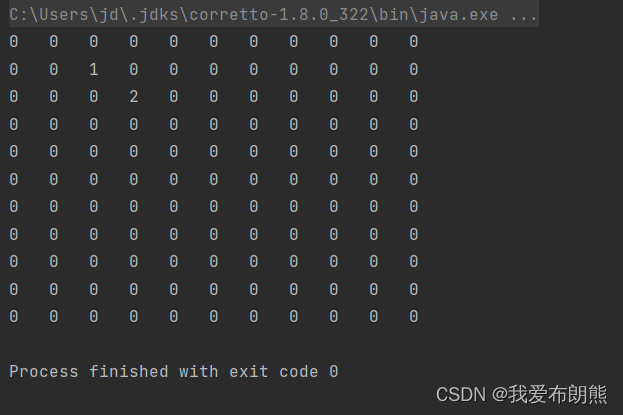
创建二维数组实现上面的那个图，1代表黑子，2表示蓝子

//        0表示无子，1表示黑子，2表示蓝子
        int chessArr1[][] = new int[11][11];
        chessArr1[1][2] = 1;
        chessArr1[2][3]=2;

//       输出原始二维数组
        for(int[] row:chessArr1){
            for(int data:row){
//                %d +制表符
                System.out.printf("%d\t",data);
            }
            System.out.println();
        }

2.2.2 原始数组转化为稀疏数组


//       转化成稀疏数组
//       遍历二维数组，找到非零数据的个数     chessArr1[0].length列数，chessArr1.length行数
        int sum = 0;
       for (int i=0;i<11;i++){    //行
           for (int j=0;j<11;j++){   //列
             if(chessArr1[i][j]!=0){
                 sum++;
             }
           }
       }
//      创建稀疏数组   sum+1表示列数
        int sparseArr[][] = new int[sum+1][3];
        sparseArr[0][0] =11;   //行
        sparseArr[0][1]=11;    //列
        sparseArr[0][2]=sum;   //不同值的个数
//      遍历二维数组，将二维数组中的有效值存放到稀松数组中
        int count =0;
        for (int i=0;i<11;i++){
            for (int j=0;j<11;j++){
                if(chessArr1[i][j]!=0){
                    count++;
                    sparseArr[count][0]=i;
                    sparseArr[count][1]=j;
                    sparseArr[count][2]=chessArr1[i][j];
                }
            }
        }

//        输出稀疏数组的形式
        for (int i=0;i<sum+1;i++){
            for (int j=0;j<3;j++){
                System.out.print(sparseArr[i][j]+"\t");
            }
            System.out.println();
        }

2.2.3 稀疏数组转化为原始数组

        int chessArr2[][] = new int[sparseArr[0][0]][sparseArr[0][1]];
//      遍历稀疏数组，取数据
        for (int i=1 ; i<sparseArr.length;i++){
            chessArr2[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];
        }
        for(int[] row:chessArr2){
            for(int data:row){
//                %d +制表符
                System.out.printf("%d\t",data);
            }
            System.out.println();
        }

三、队列的应用场景和介绍

有序列表，可以用数组或者链表来实现

遵循先入先出的原则。即：先存入队列的数据先要取出，后存入的要后取出（队首取数据、队尾存数据）

我们可以仔细看一下，下面的这个图，front代表队列首（头）的前一个位置（初始时指向第一个元素之前，所以是-1），rear代表队列尾，初始时都是-1

当数据进来的时候，我们发现front还是-1，rear跟着新加入的元素移动，指向新元素

当数据出去的时候，此时我们的front开始移动了，并且执行现如今最早加入的元素

简言之：front随着数据输出而改变，rear随着数据的增加而改变

3.1 数组模拟队列

3.1.1数组模拟队列的分析

我们将数据存入队列时称为“addQueue”，其中处理需要两个步骤

将尾指针往后移动：rear+1，当front == rear ，此时队列为空
若尾指针rear小于队列的最大下标maxSize-1，则将数据存入rear所指的数组元素中，否则无法存入数据。 rear==maxSize-1 时，队列存满

3.1.2 代码实现数组模拟队列

虽然我们这个地方模拟成功了，但是这个数组只能用一次，我们后面会讲环型数组，就真正的实现了队列


class ArrayQueue{
    private int maxSize;  //数组最大容量
    private int front;    //队列头
    private int rear;     //队列尾
    private int[] arr;    //该数据用于存放数据，模拟队列

    public ArrayQueue(int maxSize) {
        this.maxSize = maxSize;
        this.front=-1;    //初始时指向队列头部的前一个位置
        this.rear=-1;     //执行队列的尾部，即就是队列的最后一个数据
        arr = new int[maxSize];
    }

//   判断队列是否满
    public boolean isFull(){
//           相等true就是满了
        return  rear == maxSize-1;
    }

//  判断队列是否为空
    public boolean isEmpty(){
        return rear == front;
    }

//   添加数据到队列
    public void addQueue(int n){
//        判断队列是否满了
        if(isFull()){
            System.out.println("队列满了，不能加入数据");
            return;
        }
        rear++; //让rear后移动
        arr[rear]=n;
    }

//   获取队列的数据
    public int getQueue(){
//        判断是否是空
        if(isEmpty()){
//            是空，不能取数据   抛出一个异常
            throw new RuntimeException("队列已空，不能获取数据");

        }
        front++;  //后移动

        return  arr[front];
    }

//    展示队列的所有数据
    public void showQueue(){
//        遍历
        if(isEmpty()){
            System.out.println("队列空的，无法遍历");
            return;
        }
       for(int i =0;i<arr.length;i++){
           System.out.println(arr[i]);
       }
    }

//    显示队列的头数据，不是取出数据
    public int headQueue(){
        if (isEmpty()){
            System.out.println("队列空，没有数据");
            throw new RuntimeException("队列空，没有数据");
        }
        return arr[front+1];
    }


}

测试程序

public class ArrayQueueDemo {
    public static void main(String[] args) {
       ArrayQueue arrayQueue = new ArrayQueue(3);
       char key =' ';
       Scanner scanner = new Scanner(System.in);
       boolean loop = true;
       while(loop){
           System.out.println("s(show):显示队列");
           System.out.println("e(exit):退出程序");
           System.out.println("a(add):添加数据到队列");
           System.out.println("g(get):从队列取出数据");
           System.out.println("h(head):查看队列头的数据");
           key =scanner.next().charAt(0);//接受一个字符
           switch (key){
               case 's':
                   arrayQueue.showQueue();
                   break;
               case 'a':
                   System.out.println("请输出一个数");
                   int value = scanner.nextInt();
                   arrayQueue.addQueue(value);
                   break;
               case 'g':
//                  取数据
                   try{
                     int res =  arrayQueue.getQueue();
                       System.out.println("取出的数据是："+res);
                   }catch (Exception e){
                       System.out.println(e.getMessage());
                   }
                   break;
               case 'h':
                   try{
                    int res =  arrayQueue.headQueue();
                       System.out.println("队列头的数据是"+res);
                   }catch (Exception e){
                       System.out.println(e.getMessage());
                   }
                   break;
               case 'e':
                   scanner.close();
                   loop=false;
                   break;

               default:
                   break;
           }
          
       }
        System.out.println("程序退出");
    }
}

3.2 环型队列思路分析图

刚刚我们用数组实现的队列只能使用一次，没有达到复用的效果，下面我们将这个数组使用算法，改进成一个环型的队列

front 变量的含义做一个调整： front 就指向队列的第一个元素, 也就是说 arr[front] 就是队列的第一个元素 front 的初始值 = 0
rear 变量的含义做一个调整：rear 指向队列的最后一个元素的后一个位置. 因为希望空出一个空间做为约定（这个地方一定要读明白，有些算法可以不预留，看个人习惯）。rear 的初始值 = 0
当队列满时，条件是 (rear + 1) % maxSize == front 【满】
对队列为空的条件， rear == front 空
当我们这样分析，队列中有效的数据的个数 (rear + maxSize - front) % maxSize // rear = 1 front = 0

先解释一下上面队列满的时候的条件(rear + 1) % maxSize == front 【满】

我们直接把环型队列想想成一个环状，看下面的分析

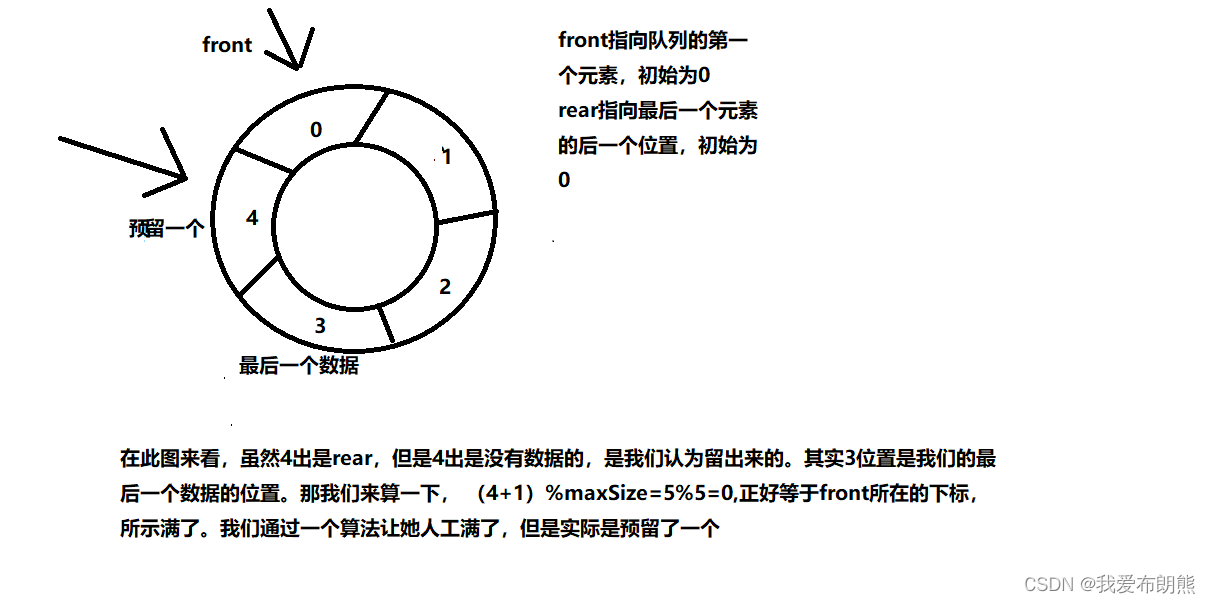
按照上面进行修改，就可以得到一个环型队列

3.2.1 环型队列实现

通过取模的方式实现


class  CircleArray{
    private int maxSize;  //数组最大容量
    private int front ;    //队列头  执行第一个元素，初始值0
    private int rear=0;     //队列尾  执行最后一个元素的下一个位置，初始值0
    private int[] arr;    //该数据用于存放数据，模拟队列

    public CircleArray(int maxSize) {
        this.maxSize = maxSize;
        this.front=0;    //初始时指向队列头部的前一个位置
        this.rear=0;     //执行队列的尾部，即就是队列的最后一个数据
        arr = new int[maxSize];
    }

//  判断队列是否满
    public boolean isFull(){
//           相等true就是满了
        return  (rear+1)%maxSize == front;
    }

//  判断队列是否为空  代码没有变化
    public boolean isEmpty(){
        return rear == front;
    }

//  添加数据到队列
    public void addQueue(int n){
//        判断队列是否满了
        if(isFull()){
            System.out.println("队列满了，不能加入数据");
            return;
        }
//      先加入，再移动
        arr[rear]=n;
//      但是往后移动的时候需要考虑是否满了，不能让rear超过最大限度，否则数组不支持
        rear = (rear+1)%maxSize;

    }


//  获取队列的数据，出队
    public int getQueue(){
//        判断是否是空
        if(isEmpty()){
//            是空，不能取数据   抛出一个异常
            throw new RuntimeException("队列已空，不能获取数据");

        }
//      这里需要分析出front指向的元素是队列的第一个元素
//           把front对应的值保存到一个临时变量
//           将front后移动
//           将临时变量返回
        int value = arr[front];
        front = (front+1)%maxSize;
       return value;
    }


//  展示队列的所有数据
    public void showQueue(){
//        遍历
        if(isEmpty()){
            System.out.println("队列空的，无法遍历");
            return;
        }
//      从front开始遍历，遍历多少个元素
        for(int i =front;i<front+size();i++){
//          这个地方要动脑筋，画个图自己看看
            System.out.println(arr[i%maxSize]);
        }
    }

//   求出当前队列的有效数据个数
    public int size(){
        return (rear+maxSize-front)%maxSize;
    }

//  显示队列的头数据，不是取出数据
    public int headQueue(){
        if (isEmpty()){
            System.out.println("队列空，没有数据");
            throw new RuntimeException("队列空，没有数据");
        }
        return arr[front];
    }
}