5.5.2 并查集（双亲表示法）

1. 并查集的存储结构

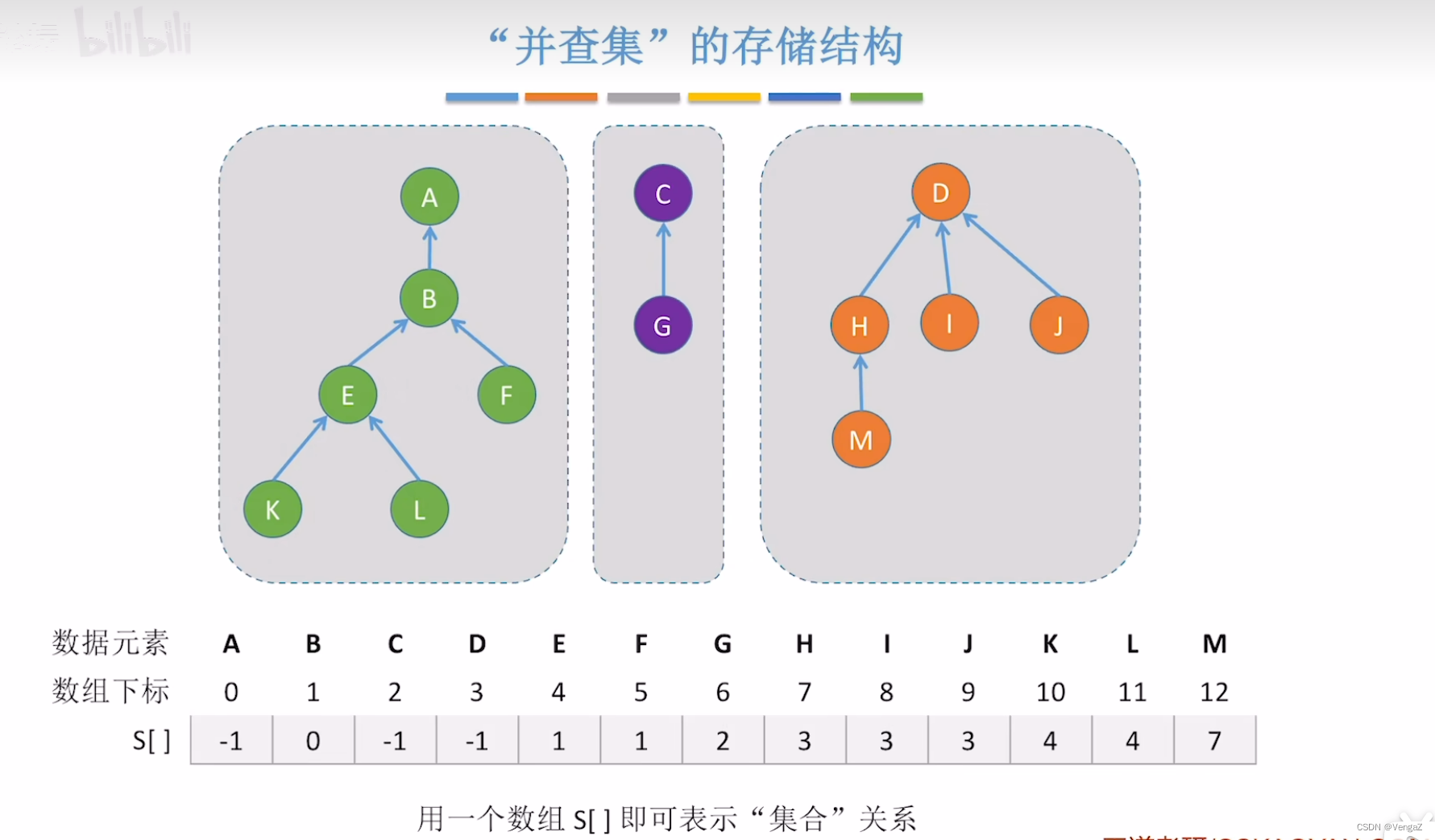
2. 并查集的代码实现

初始化

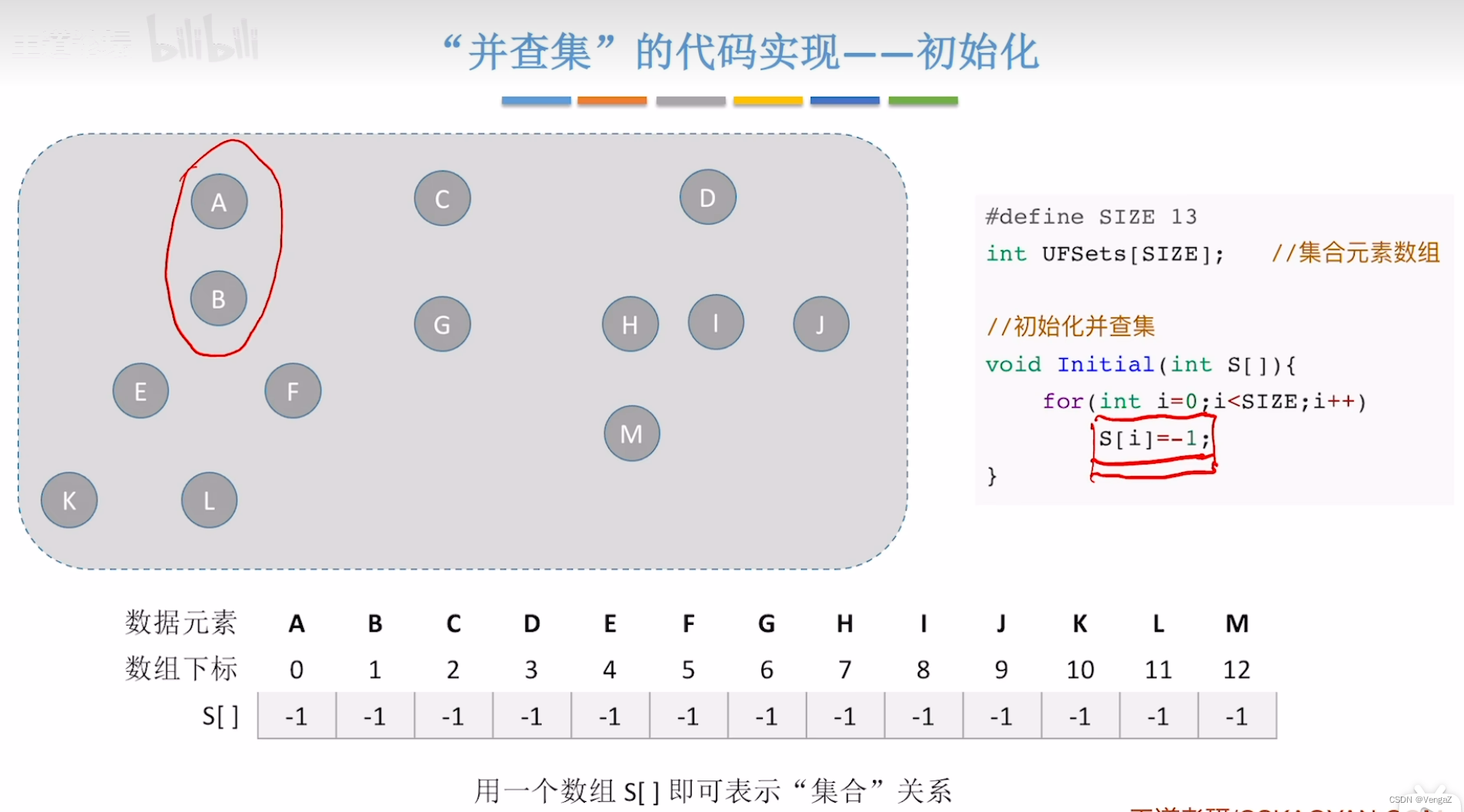
并查

时间复杂度

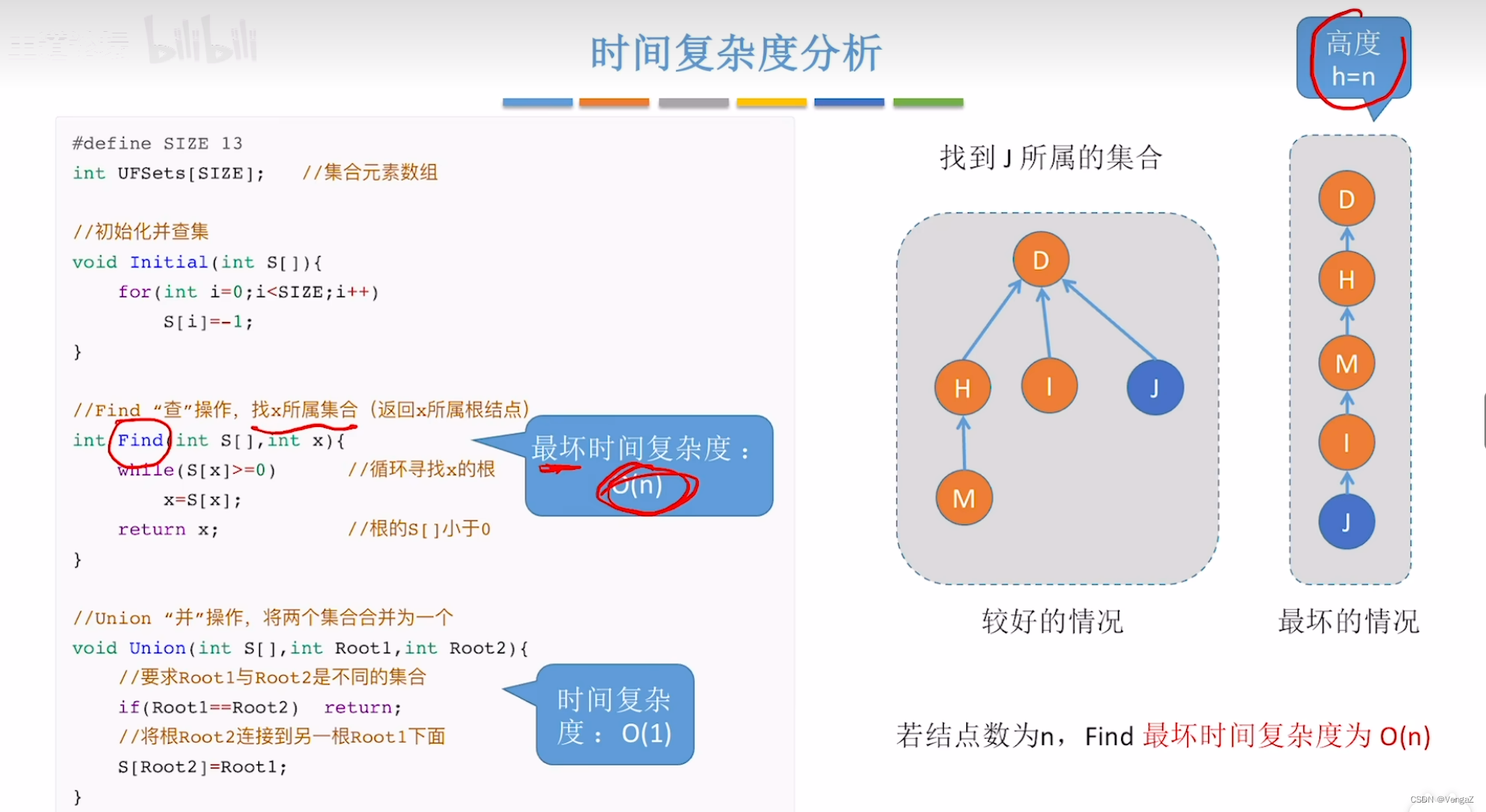
union操作的优化（不要瘦高的树）

并查集的进一步优化（find的优化，压缩路径）

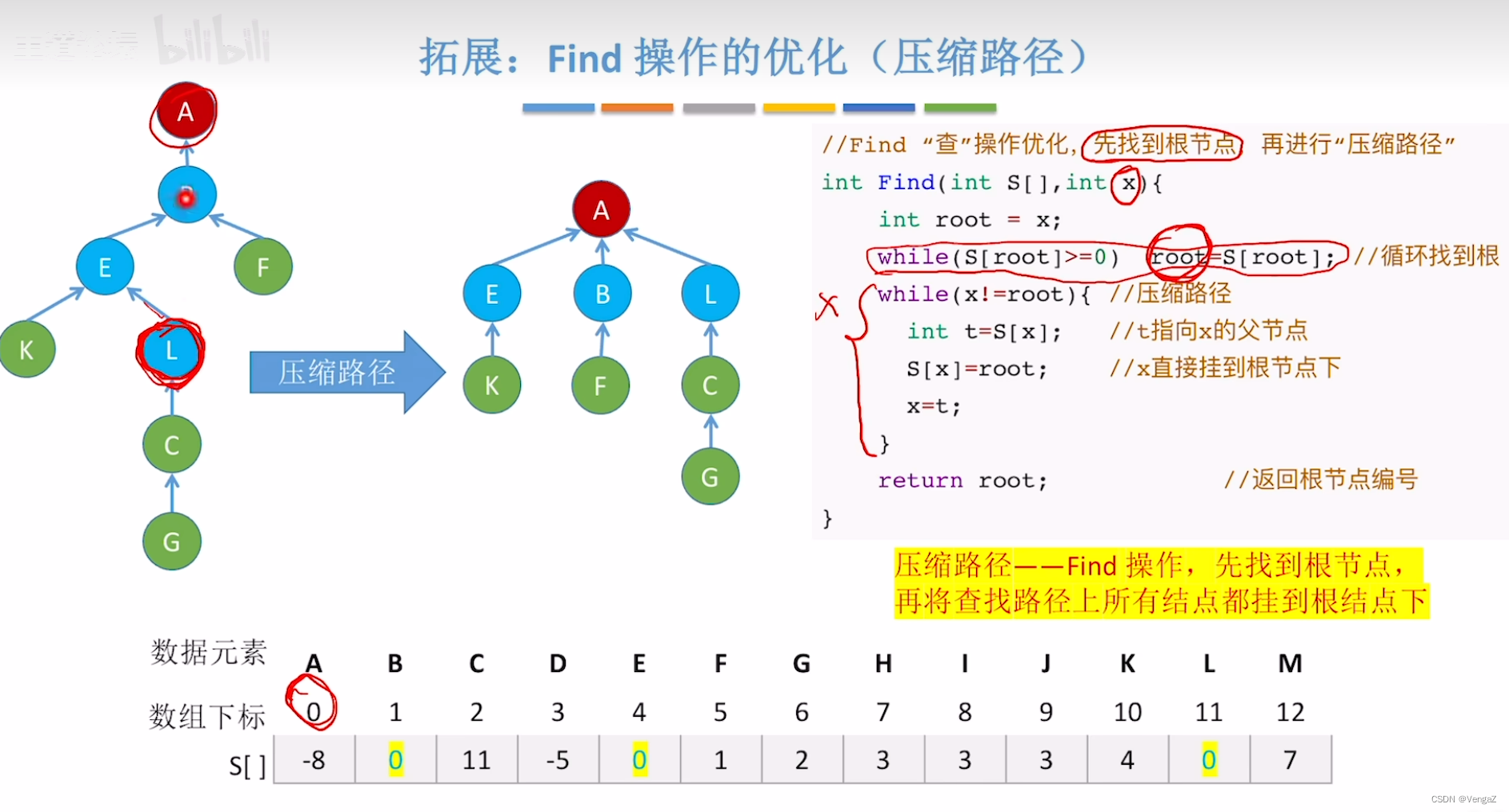
优化总结

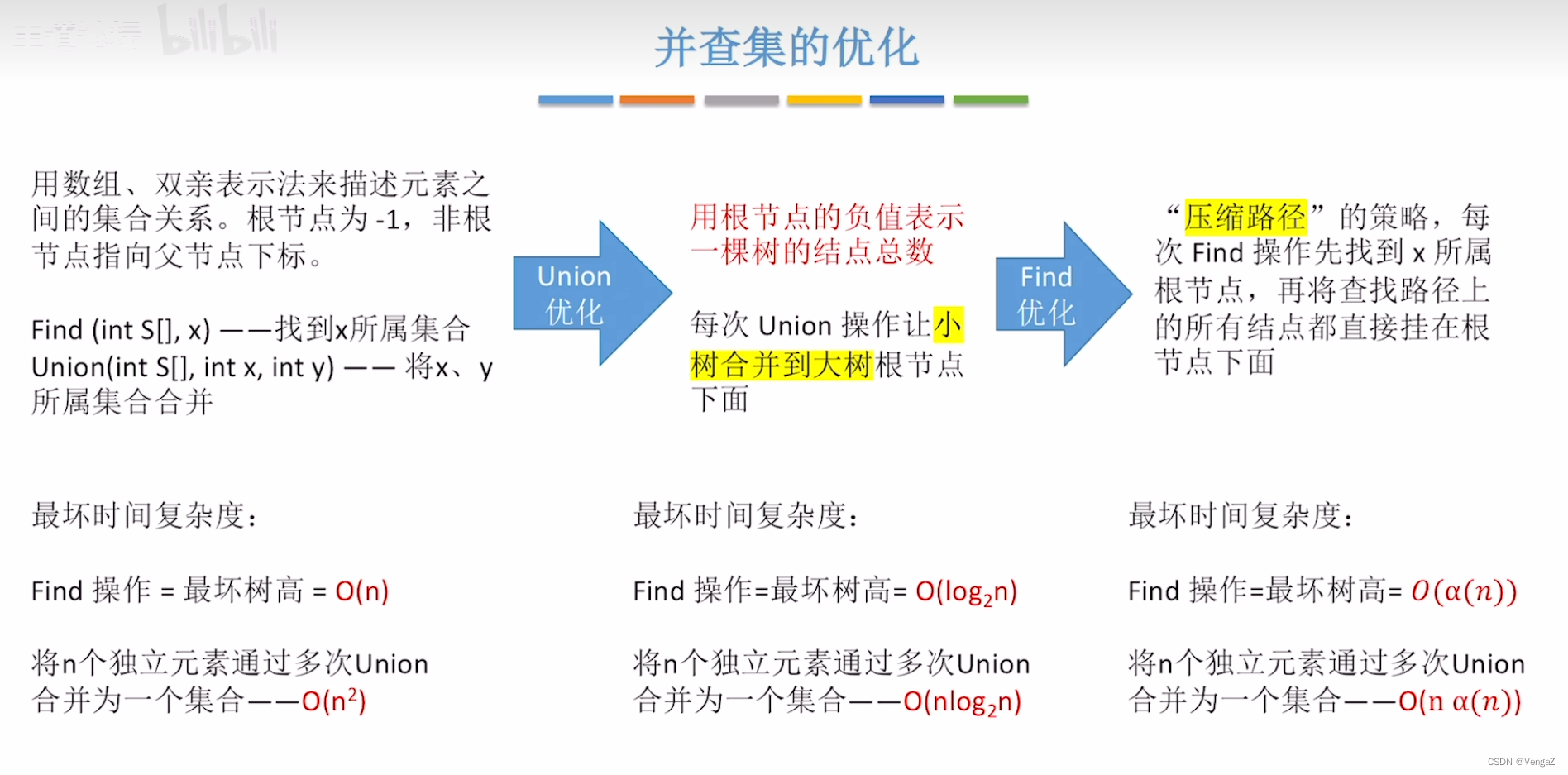
数据结构：并查集（Disjoint-Set）

在计算机科学中，并查集是一种用于处理集合合并与查询问题的数据结构。它主要用于解决一些实际问题中的集合合并和查询问题，如网络连接问题、社交网络中的好友关系、图论中的连通性问题等。并查集是一种高效的数据结构，能够在常数时间内执行合并和查询操作。

并查集的基本操作

并查集主要包含以下两个基本操作：

1. 查找（Find）：查找操作用于确定元素所属的集合，即查找元素所在的根节点（代表元素）。如果两个元素的根节点相同，则表示它们属于同一个集合。

2. 合并（Union）：合并操作用于将两个集合合并为一个集合，即将两个元素所在的集合合并为一个新的集合。合并操作的核心是将其中一个集合的根节点指向另一个集合的根节点，以实现合并。

并查集的实现

并查集可以通过数组和树结构来实现。其中，数组实现是比较简单的方式，但效率相对较低。树结构的实现包括：普通树结构和优化的树结构。

1. 数组实现并查集

数组实现并查集是一种简单而直观的方式，其中每个元素在数组中对应一个父节点。初始时，每个元素的父节点指向自己，表示它们各自构成一个独立的集合。

合并操作可以通过修改数组中某个元素的父节点来实现。例如，将元素A所在的集合合并到元素B所在的集合，只需要将A的父节点指向B即可。

查找操作可以通过递归或循环遍历找到元素所在集合的根节点，直到根节点的父节点指向自己为止。

数组实现并查集的效率相对较低，特别是在查找操作中可能需要较多的遍历操作。

2. 普通树结构实现并查集

普通树结构实现并查集是在数组实现的基础上，将每个集合构造为一棵树结构。合并操作将一个树的根节点链接到另一个树的根节点，从而实现集合的合并。

但是，普通树结构的并查集在处理合并操作时，可能会出现树不平衡的情况，即某个集合的树高度过高，影响了查找操作的效率。

3. 优化的树结构实现并查集

为了优化并查集的性能，在普通树结构的基础上引入了路径压缩和按秩合并两种优化方法。

• 路径压缩：在执行查找操作时，将当前节点到根节点的路径上的所有节点直接链接到根节点，从而减少查找操作中的遍历次数，提高查找效率。

• 按秩合并：在执行合并操作时，将高度较低的树合并到高度较高的树上，从而避免了树的不平衡，提高了合并操作的效率。

优化的树结构实现并查集能够在常数时间内完成合并和查找操作，具有较高的效率和性能。

原理

并查集的基本原理是通过树结构来表示集合，并使用树的根节点来代表集合的代表元素。每个节点表示一个元素，而树的根节点表示该集合的代表元素。在并查集中，每个集合是一棵树，树中的节点通过指针连接。

并查集主要包含两个基本操作：合并和查询。

• 合并操作：将两个不相交的集合合并成一个集合，即将两个树的根节点连接在一起。
• 查询操作：判断两个元素是否属于同一个集合，即判断它们的根节点是否相同。

应用场景

并查集广泛应用于解决具有等价关系的问题，例如：

• 社交网络中的好友关系，判断两个用户是否在同一个社交圈子中。
• 图像处理中的连通区域，判断图像中的像素是否属于同一个区域。
• 岛屿数量问题，判断地图中岛屿的个数和是否相连。

代码实现

在实现并查集时，我们需要定义一个节点结构来表示每个元素，并编写合并和查询操作的函数。

首先，定义一个节点结构：

class Node:
    def __init__(self, data):
        self.data = data
        self.parent = self
        self.rank = 0

在初始化时，每个节点的父节点都是它自己，表示每个节点都是一个单独的集合。rank表示树的高度，用于优化合并操作。

接下来，实现合并和查询操作的函数：

def find(node):
    if node != node.parent:
        node.parent = find(node.parent)
    return node.parent

def union(node1, node2):
    root1 = find(node1)
    root2 = find(node2)
    if root1 == root2:
        return

    if root1.rank > root2.rank:
        root2.parent = root1
    elif root1.rank < root2.rank:
        root1.parent = root2
    else:
        root1.parent = root2
        root2.rank += 1

在find函数中，使用路径压缩来优化查询操作，将节点的父节点直接设为根节点，加快下一次查询的速度。

在union函数中，通过rank来优化合并操作，将高度较低的树连接到高度较高的树上，使得整个树结构更加平衡。

结论

并查集是一种用于处理集合合并与查询问题的高效数据结构。它在解决网络连接、社交网络、图论等问题时具有重要的应用价值。在实际应用中，根据具体的场景和需求，我们可以选择不同的实现方式，如数组实现、普通树结构实现或优化的树结构实现，并根据情况选择合适的优化方法，以获得更高的执行效率和性能。