目录
一、选择题
二、编程题
三、选择题题解
四、编程题题解
一、选择题
1、2 —3—6—7—8—14—15—30,下面的数字哪一个是不属于这组数字的系列?
A. 3
B. 7
C. 8
D. 15
2、下列关于线性链表的叙述中,正确的是( )
A. 各数据结点的存储空间可以不连续,但它们的存储顺序与逻辑顺序必须一致
B. 各数据结点的存储顺序与逻辑顺序可以不一致,但它们的存储空间必须连续
C. 进行插入与删除时,不需要移动表中的元素
D. 以上说法均不正确
3、下列描述的不是链表的优点是( )
A. 逻辑上相邻的结点物理上不必邻接
B. 插进、删除运算操纵方便,不必移动结点
C. 所需存储空间比线性表节省
D. 无需事先估计存储空间的大小
4、向一个栈顶指针为h的带头结点的链栈中插入指针s所指的结点时,应执行()
A. h->next=s;
B. s->next=h;
C. s->next=h;h->next=s;
D. s->next=h->next;h->next=s;
5、队列{a,b,c,d,e}依次入队,允许在其两端进行入队操作,但仅允许在一端进行出队操作,则不可能得到的出队序列是()
A. b, a, c, d, e
B. d, b, a, c, e
C. d, b, c, a, e
D. e, c, b, a, d
6、若一棵二叉树具有12个度为2的结点,6个度为1的结点,则度为0的结点个数是()
A. 10
B. 11
C. 13
D. 不确定
7、下列各树形结构中,哪些是平衡二叉查找树:
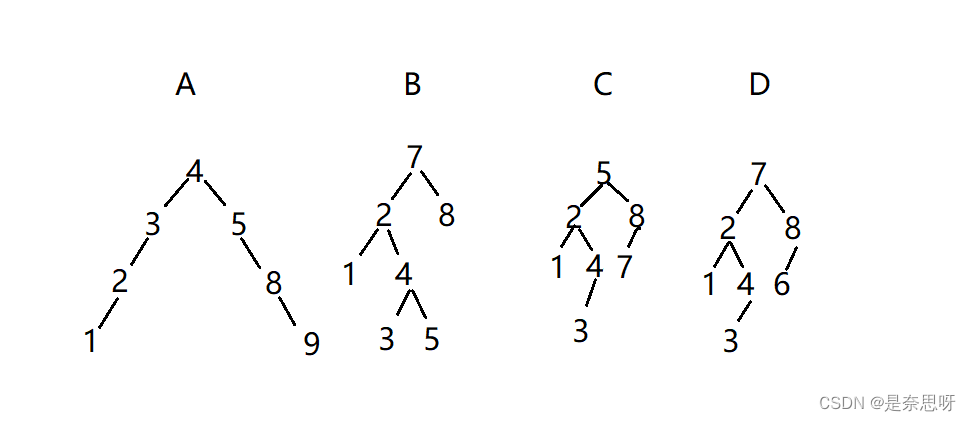
8、已知关键字序列5,8,12,19,28,20,15,22是最小堆,插入关键字3,调整后得到的最小堆是()
A. 3,8,12,5,20,15,22,28,19
B. 3,5,12,19,20,15,22,8,28
C. 3,12,5,8,28,20,15,22,19
D. 3,5,12,8,28,20,15,22,19
9、采用哈希表组织100万条记录,以支持字段A快速查找,则()
A. 理论上可以在常数时间内找到特定记录
B. 所有记录必须存在内存中
C. 拉链式哈希曼最坏查找时间复杂度是O(n)
D. 哈希函数的选择跟A无关
10、假设你只有100Mb的内存,需要对1Gb的数据进行排序,最合适的算法是()
A. 归并排序
B. 插入排序
C. 快速排序
D. 冒泡排序
二、编程题
1、微信红包 题目链接
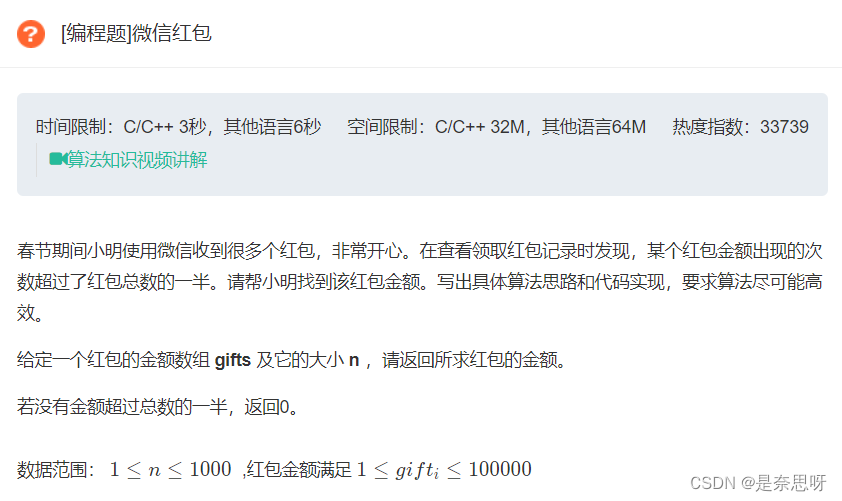
2、计算字符串的编辑距离 题目链接

三、选择题题解
1、2 —3—6—7—8—14—15—30,下面的数字哪一个是不属于这组数字的系列?
A. 3
B. 7
C. 8
D. 15
正确答案:C
题解:
这题小编也看懵了,但据网上搜索,解析是这样的,去掉8以后,从第一个数字开始,依次+1,*2;2+1=3,3*2=6,6+1=7,7*2=14,14+1=15,15*2=30;
2、下列关于线性链表的叙述中,正确的是( )
A. 各数据结点的存储空间可以不连续,但它们的存储顺序与逻辑顺序必须一致
B. 各数据结点的存储顺序与逻辑顺序可以不一致,但它们的存储空间必须连续
C. 进行插入与删除时,不需要移动表中的元素
D. 以上说法均不正确
正确答案:C
题解:
链表的插入与删除操作均不会影响别的结点的位置,C正确;A与B中,链表数据的存储位置是不连续的且存储顺序与逻辑顺序也不一定一致;
3、下列描述的不是链表的优点是( )
A. 逻辑上相邻的结点物理上不必邻接
B. 插进、删除运算操纵方便,不必移动结点
C. 所需存储空间比线性表节省
D. 无需事先估计存储空间的大小
正确答案:C
题解:
C选项,恰恰相反,线性表比链表更节省空间,因此链表中不仅需要存储数据,还需要存储下一个结点的信息指针;
4、向一个栈顶指针为h的带头结点的链栈中插入指针s所指的结点时,应执行()
A. h->next=s;
B. s->next=h;
C. s->next=h;h->next=s;
D. s->next=h->next;h->next=s;
正确答案:D
题解:
链式栈栈顶指针一般在链表头结点,即头插,正确代码D;
5、队列{a,b,c,d,e}依次入队,允许在其两端进行入队操作,但仅允许在一端进行出队操作,则不可能得到的出队序列是()
A. b, a, c, d, e
B. d, b, a, c, e
C. d, b, c, a, e
D. e, c, b, a, d
正确答案:C
题解:
A选项,我们可以先插入a,然后从队头插入b,接着从队尾分别插入c,d,e;B选项,先插入a,然后队头插入b,队尾插入c,队头插入d,队尾插入e;C选项错误;D选项,先插入a,然后队头插入b,c,接着队尾插入d,最后队头插入e;
6、若一棵二叉树具有12个度为2的结点,6个度为1的结点,则度为0的结点个数是()
A. 10
B. 11
C. 13
D. 不确定
正确答案:C
题解:
根据特性公式,n0 = n2 + 1;
7、下列各树形结构中,哪些是平衡二叉查找树:

正确答案:C
题解:
平衡二叉排序树的特性是对于每个结点来说,左子树的所有结点都小于根结点,右子树的所有结点都大于根节点,且左右子树高度差不超过1;
8、已知关键字序列5,8,12,19,28,20,15,22是最小堆,插入关键字3,调整后得到的最小堆是()
A. 3,8,12,5,20,15,22,28,19
B. 3,5,12,19,20,15,22,8,28
C. 3,12,5,8,28,20,15,22,19
D. 3,5,12,8,28,20,15,22,19
正确答案:D
题解:
具体调节如下图所示;

9、采用哈希表组织100万条记录,以支持字段A快速查找,则()
A. 理论上可以在常数时间内找到特定记录
B. 所有记录必须存在内存中
C. 拉链式哈希曼最坏查找时间复杂度是O(n)
D. 哈希函数的选择跟A无关
正确答案:C
题解:
A选项,不一定能在常数时间找到特定记录,没有考虑冲突问题;B选项,记录也可以存储在外存中;C选项,正确,可能会挂在同一个桶下;D选项,有关;
10、假设你只有100Mb的内存,需要对1Gb的数据进行排序,最合适的算法是()
A. 归并排序
B. 插入排序
C. 快速排序
D. 冒泡排序
正确答案:A
题解:
只有归并排序才存在外排序一说;
四、编程题题解
1、微信红包
思路:这是一个经典的查找众数的题目,众数的特点是超过所有数的一半,若我们随机选择一个数为众数,每遇到一个数是否为众数,若是则计数count++;若不是且count不为0,则count--,若不是且count为0,则更换众数,最坏条件下,我们剩下的那个数也是众数
class Gift
{
public:
int getValue(vector<int> gifts, int n)
{
// 众数
int candidate = -1;
int count = 0;
for (auto e : gifts)
{
if(count == 0)
{
candidate = e;
count = 1;
}
else
{
if(candidate == e)
count++;
else
count--;
}
}
count = 0;
for(auto e : gifts)
if(e == candidate)
count++;
if(count > (n / 2))
return candidate;
else
return 0;
}
};2、计算字符串的编辑距离
思路:这是一道经典的dp问题;题目要求我们算出两个字符串的最小编辑距离;我们首先根据经验推导出这题的dp状态为dp[ i ][ j ],代表把以 i 结尾字符串str1通过最小的编辑距离到以 j 结尾的字符串str2;

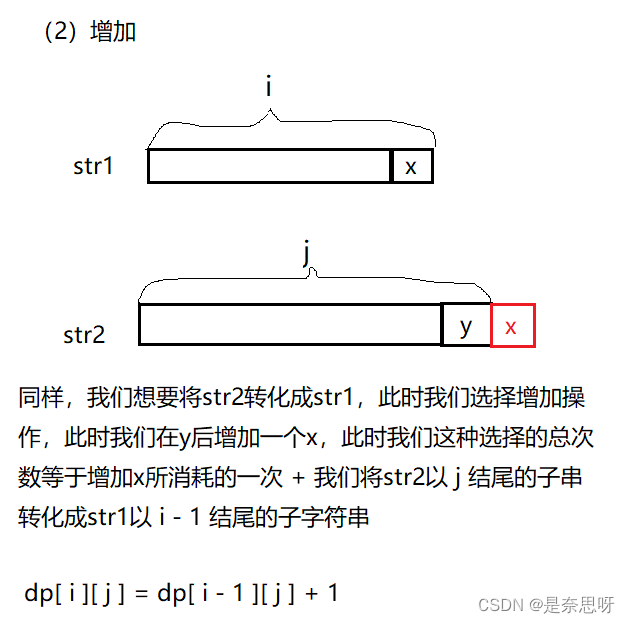
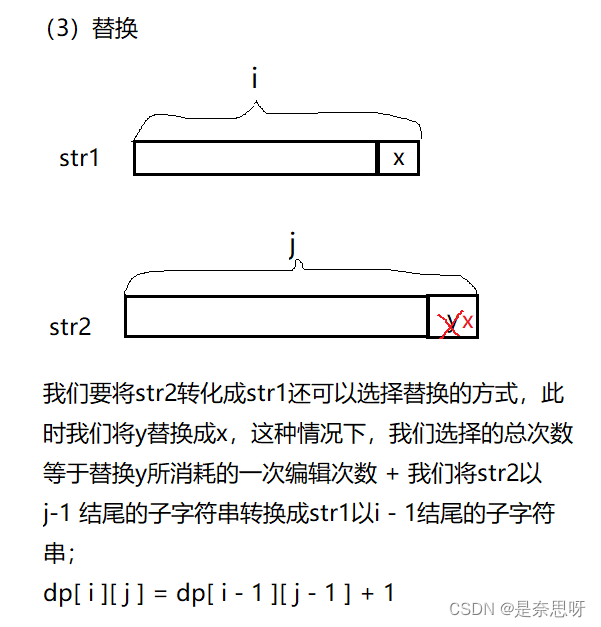
对上述情况推导方程总结;

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int get_min_edit(const string& str1, const string& str2)
{
if(str1.empty() || str2.empty())
return min(str1.size(), str2.size());
int len1 = str1.size();
int len2 = str2.size();
vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));
// 初始化
for(int i = 0; i <= len1; i++)
dp[i][0] = i;
for(int j = 0; j <= len2; j++)
dp[0][j] = j;
// 填表
for(int i = 1; i <= len1; i++)
{
for(int j = 1; j <= len2; j++)
{
if(str1[i - 1] == str2[j - 1])
dp[i][j] = dp[i - 1][j - 1];
else
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
}
}
return dp[len1][len2];
}
int main()
{
string str1, str2;
cin >> str1 >> str2;
cout << get_min_edit(str1, str2) << endl;
return 0;
}