题目

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：1

示例 2：

输入：n = 5
输出：5

提示：

0 <= n <= 100

解题思路

1.题目要求我们求斐波那契（Fibonacci）数列的第 n 项和，还给出了递归公式，那我们想到的第一种方法可能就是递归，像这样。
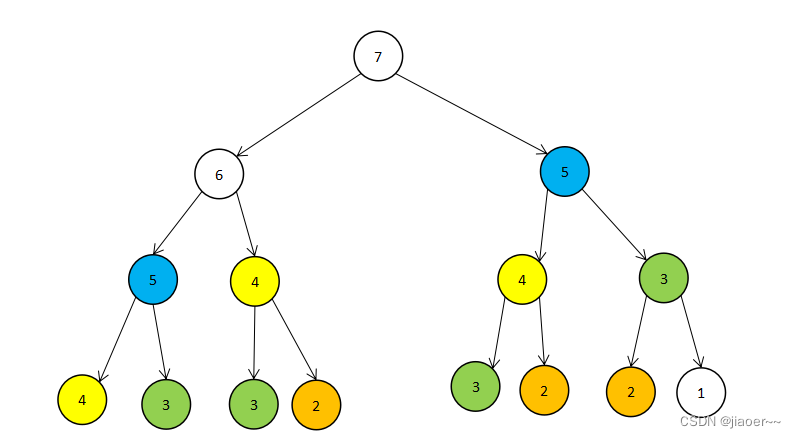
class Solution {
    public int fib(int n) {
        if(n <= 1){
            return n;
        }
        return fib(n - 1) + fib(n - 2);

    }
}
但是这种方法会超出时间限制，因为它做了很多重复的工作

相同元素的f（n），每当我们在用到的时候就会将其重新算一遍，所以这种方法会超出时间限制。

2.那么我们还有没有优化的方法呢？当时是有的，我们可以新建一个数组在对应下标的位置存储一下对应f（n）的值，这样我们只需要计算一次，下次在用到时可以直接从数组中拿取。

3.首先我们新建一个数组，将其中的值都初始化为 -1，然后新建一个f（n）函数去进行运算，如果 n <= 1 的我们可以直接返回n，否则我们需要去数组中查找下标为n时的arr[n]是否为 -1，若为 -1 则说明我们还没有计算，我们就需要进行计算 f(n - 1) + f(n - 2) ，题目要求我们需要取模不要忘记了，然后将计算出的结果存放在数组相应的位置以便下次使用，最后返回计算结果即可。

代码实现

class Solution {
    int[] arr;
    public int fib(int n) {
        arr = new int[n+1];
       for(int i = 0; i <= n; i++){
           arr[i] = -1;
       }
       return f(n);

    }
    public int f(int n){
        if(n <= 1){
            return n;
        }
        if(arr[n] != -1){
            return arr[n];
        }
        int sum = (f(n - 1) + f(n - 2)) % 1000000007;
        arr[n] = sum;
        return sum;
    }
}