引言

1 pytorch中Tensor

1.1 什么是Tensor

1.2 为什么需要Tensor

1.3 如何创建Tensor

1.3.1 从已有其他数据结构转化创建为Tensor

1.3.2 随机初始化一个Tensor

1.3.3 从已保存文件加载一个Tensor

1.4 Tensor的特性

1.4.1 丰富的常用函数操作

1.4.2 灵活的dtype和CPU/GPU自由切换

1.4.3 自动梯度求解

2 Numpy

2.1 什么是Numpy

2.2 NumPy有哪些优势

2.2.1 ndarray支持并行化运算（向量化运算）

2.2.2 效率远高于纯Python代码

2.2.3 存储数据地址连续

2.3 如何创建Numpy对象

2.3.1 使用Numpy创建ndarray数组

2.3.2 查看数组维数并改变维度

2.3.3 通过ndarray的属性也可以操作数组

2.3.4 创建元素均为 0 的数组

2.3.4 创建1填充的指定形状大小与数据类型的新数组

2.3.5 将一个 Python 序列转化为 ndarray 对象

2.3.6 使用指定的缓冲区创建数组

2.3.7 迭代对象转换为 ndarray 数组

2.3.8 创建给定数值范围的数组

2.3.9 创建指定的数值区间内的数组

2.3.10 创建等比数组

2.4 Numpy运算

2.4.1 平铺数组元素

2.4.2 以一维数组的形式返回一份数组副本

2.4.2 转化成连续的扁平数组

2.4.3 Numpy 的位运算

2.4.4 算术运算

2.4.5 Numpy矩阵操作

2.4.5 两个矩阵的逐元素乘法

2.4.6 两个数组的矩阵乘积

2.4.7 两个矩阵的点积

2.4.8 两个矩阵内积

2.4.9 解线性矩阵方程

2.4.10 计算矩阵的逆矩阵

3 Tensor和Numpy的相互转换

3.1 Tensor转Numpy

3.2 Numpy转Tensor

3.2.1 使用torch.tensor

3.2.2 使用torch.from_numpy

4 Tensor转其他

4.1 Tensor转数值

4.2 Tensor转List

4.3 Tensor转List Tensor

引言

在我们构建深度学习模型的过程中，Tensor和Numpy必不可少，而且经常会面临两种数据结构的相互转换。

这两个数据结构到底有什么区别？
什么时候选择哪种数据结构使用？
两种数据结构之间如何转换？

本文通过定义、应用场景、转换方式等多个维度，给出问题的答案。

1 pytorch中Tensor

1.1 什么是Tensor

Tensor是深度学习中最为基础也最为关键的数据结构：

Tensor之于PyTorch就好比是array之于Numpy或者DataFrame之于Pandas，都是构建了整个框架中最为底层的数据结构；
Tensor与普通的数据结构不同，具有一个极为关键的特性——自动求导。

定义：Tensor英文原义是张量，在Pytorch官网中对其有如下介绍：

一个Tensor是一个包含单一数据类型的高维矩阵，一般而言，描述Tensor的高维特性通常用三维及以上的矩阵来描述，例如下图所示：单个元素叫标量（scalar），一个序列叫向量（vector），多个序列组成的平面叫矩阵（matrix），多个平面组成的立方体叫张量（tensor）。当然，就像矩阵有一维矩阵和二维矩阵乃至多维矩阵一样，张量也无需严格限制在三维以上才叫张量，在深度学习的范畴内，标量、向量和矩阵都统称为张量。

Tensor也不是PyTorch特有的定义，而是众多深度学习框架广泛使用的数据结构，如TensorFlow。

1.2 为什么需要Tensor

PyTorch中的Tensor是深度学习中广泛使用的数据结构，本质上就是一个高维的矩阵，甚至将其理解为NumPy中array的推广和升级也不为过。但由于其支持的一些特殊特性，Tensor在用于支撑深度学习模型和训练时更为便利。

1.3 如何创建Tensor

一般而言，创建一个Tensor大体有三种方式：

从已有其他数据结构转化创建为Tensor
随机初始化一个Tensor
从已保存文件加载一个Tensor

1.3.1 从已有其他数据结构转化创建为Tensor

这可能是实际应用中最常用的一种形式，常用于数据集的加载，比如从一个列表、从一个NumPy的array中读取数据，而后生成一个新的Tensor。为了实现这一目的，常用的有两种方式：

torch.tensor
torch.Tensor

二者的区别就是前者用的是tensor函数（t是小写），后者用的是Tensor类（T是大写）。二者在创建Tensor的默认数据类型、支持传参以及个别细节的处理方面。

首先是创建的Tensor默认数据类型不同：

import torch

t1 = torch.tensor([1,2,3])
t2 = torch.Tensor([1,2,3])
print(t1, t2)
print(t1.dtype, t2.dtype)

运行显示如下：

tensor([1, 2, 3]) tensor([1., 2., 3.])
torch.int64 torch.float32

其次，应用Tensor类初始化输入一个整数将返回一个以此为长度的全零一维张量，而tensor函数则返回一个只有该元素的零维张量：

import torch

t1 = torch.tensor(3)
t2 = torch.Tensor(3)
print(t1, t2)

运行结果显示：

tensor(3) tensor([0., 0., 0.])

有一个细节需要优先提及：应用Tensor类接收一个序列创建Tensor时，返回的数据类型为float型，这是因为Tensor是FloatTensor的等价形式，即除此之外还有ByteTensor，IntTensor，LongTensor以及DoubleTensor等不同的默认数据类型。

基于已有数据创建Tensor另外两个常用函数：

from_numpy
as_tensor

二者与上述方法最大的不同在于它们返回的Tensor与原有数据是共享内存的，而前述的tensor函数和Tensor类则是copy后创建一个新的对象。

import torch
import numpy as np

n1 = np.array([1,2,3])
n2 = np.array([1,2,3])
n3 = np.array([1,2,3])
t1 = torch.tensor(n1)
t2 = torch.from_numpy(n2)
t3 = torch.as_tensor(n3)
print('t1:', t1)
print('t2:', t2)
print('t3:', t3)

n1[0] = 100
n2[0] = 100
n3[0] = 100

print('t1:', t1)
print('t2:', t2)
print('t2:', t3)

运行结果显示：

t1: tensor([1, 2, 3])
t2: tensor([1, 2, 3])
t3: tensor([1, 2, 3])
t1: tensor([1, 2, 3])
t2: tensor([100,   2,   3])
t2: tensor([100,   2,   3])

1.3.2 随机初始化一个Tensor

随机初始化是一种常用的形式，在搭建一个神经网络模型中，在添加了一个模块的背后也自动随机初始化了该模块的权重。这类方法分为两种形式：

创建一个特定类型的tensor，例如torch.ones，torch.randn等等
根据一个已有Tensor创建一个与其形状一致的特定类型tensor，例如torch.ones_like，torch.randn_like等等

import torch

func_name = [x for x in dir(torch) if x.endswith('like')]
print(func_name)

运行结果显示：

['empty_like', 'full_like', 'ones_like', 'rand_like', 'randint_like', 'randn_like', 'zeros_like']

随机构建一个PyTorch中的全连接单元Linear，其会默认创建相应的权重系数和偏置（由于网络参数一般是需要参与待后续的模型训练，所以默认requires_grad=True）：

import torch

linear = torch.nn.Linear(2,3)
print('weight:', linear.weight)
print('bias:', linear.bias)

运行结果显示：

weight: Parameter containing:
tensor([[-0.5380, -0.6481],
        [ 0.0144,  0.0627],
        [-0.6560,  0.0382]], requires_grad=True)
bias: Parameter containing:
tensor([-0.2800,  0.0235, -0.6940], requires_grad=True)

1.3.3 从已保存文件加载一个Tensor

PyTorch不会刻意区分要保存和加载的对象是何种形式，可以是训练好的网络，也可以是数据，这在Python中就是pickle，通过torch.save和torch.load两个函数实现。保存后的文件没有后缀格式要求，常用的后缀格式有 .pkl、.pth、.pt三种，此方法常用于模型以及大规模数据集的保存。

import torch

t1 = torch.tensor([1,2,3,4,5])
torch.save(t1, 'tensor.pkl')

ret_t = torch.load('tensor.pkl')
print('ret_t', ret_t)

运行结果如下：

ret_t tensor([1, 2, 3, 4, 5])

1.4 Tensor的特性

PyTorch之所以定义了Tensor来支持深度学习，而没有直接使用Python中的一个list或者NumPy中的array，是因为Tensor被赋予了一些独有的特性。Tensor的主要特性为以下三个方面：

丰富的常用操作函数
灵活的dtype和CPU/GPU自由切换存储
自动梯度求解

1.4.1 丰富的常用函数操作

Tensor本质上是一个由数值型元素组成的高维矩阵，深度学习的过程就是各种矩阵运算的过程，Tensor作为其基础数据结构支持丰富的函数操作。

Tensor自身进行操作函数，例如tensor.max(), tensor.abs()等等，
Tensor其他tensor进行相关操作，例如tensor.add()用于与另一个tensor相加，tensor.mm()用于与另一个tensor进行矩阵乘法等等。这里的相加和相乘对操作的两个tensor尺寸有所要求。

除了支持的函数操作足够丰富外，tensor的API函数还有另一个重要的便利特性：绝大多数函数都支持两个版本：带下划线版和不带下划线版，例如tensor.abs()和tensor.abs_()，二者均返回操作后的Tensor，但同时带下划线版本属于inplace操作，即调用后自身数据也随之改变。

1.4.2 灵活的dtype和CPU/GPU自由切换

Tensor中dtype的概念类似于NumPy和Pandas中的用法，用于指定待创建Tensor的数据结构。PyTorch中定义了10种不同的数据结构，包括不同长度的整型、不同长度的浮点型，整个Tesor的所有元素必须数据类型相同，且必须是数值类型（NumPy中的array也要求数组中的元素是同质的，但支持字符串类型的）：

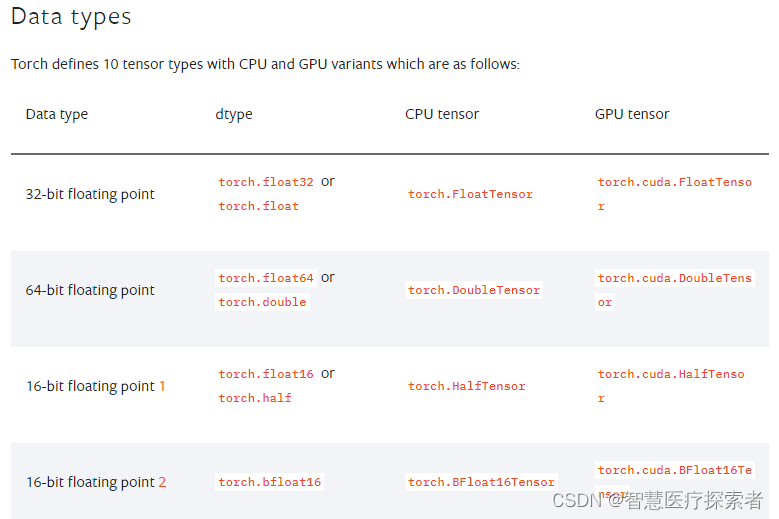
除了支持不同的数值数据类型外，Tensor的另一大特色是其支持不同的计算单元：CPU或GPU，支持GPU加速也是深度学习得以大规模应用的一大关键。为了切换CPU计算（数据存储于内存）或GPU计算（数据存储于显存），Tensor支持灵活的设置存储设备，包括如下两种方式：

创建tensor时，通过device参数直接指定
通过tensor.to()函数切换，to()既可用于切换存储设备，也可切换数据类型

此外，除了dtype和device这两大特性之外，其实Tensor还有第三个特性，即layout，布局。主要包括strided和sparse_coo两种，该特性一般不需要额外考虑。

1.4.3 自动梯度求解

Tensor自动梯度求解是支撑深度学习的基石，深度学习模型的核心是在于神经元的连接，而神经元之间连接的关键在于网络权重，也就是各个模块的参数。正因为网络参数的不同，所以才使得相同的网络结构能实现不同的模型应用价值。那么，如何学习最优网络参数呢？这就是深度学习中的的优化利器：梯度下降法，而梯度下降法的一大前提就是支持自动梯度求解。

Tensor为了支持自动梯度求解，大体流程如下：

Tensor支持grad求解，即requires_grad=True
根据Tensor参与计算的流程，将Tensor及相应的操作函数记录为一个树结构（或称之为有向无环图：DAG），计算的方向为从叶节点流向根节点
根据根节点Tensor与目标值计算相应的差值（loss），然后利用链式求导法则反向逐步计算梯度（也即梯度的反向传播）

2 Numpy

2.1 什么是Numpy

Numpy 是 Numerical Python 的缩写，它是一个由多维数组对象（ndarray）和处理这些数组的函数（function）集合组成的库。使用 Numpy 库，可以对数组执行数学运算和相关逻辑运算。Numpy 不仅作为 Python 的扩展包，它同样也是 Python 科学计算的基础包。Numpy 提供了大量的数学函数，主要用来计算、处理一维或多维数组，支持常见的数组和矩阵操作。NumPy 的底层主要用 C语言编写，因此它能够高速地执行数值计算。Numpy 还提供了多种数据结构，这些数据结构能够非常契合的应用在数组和矩阵的运算上。
Numpy 作为一个开源项目，它由许多协作者共同开发维护，随着数据科学（Data Science，简称 DS，包括大数据分析与处理、大数据存储、数据抓取等分支）的蓬勃发展，像 Numpy、SciPy（Python科学计算库）、Pandas（基于NumPy的数据处理库）等数据分析库都有了大量的增长，它们都具有较简单的语法格式。Numpy 通常会和Matplotlib等搭配一块使用。

2.2 NumPy有哪些优势

2.2.1 ndarray支持并行化运算（向量化运算）

numpy内置了并行运算功能，当系统有多个核心时，做某种计算时，numpy会自动做并行计算。

2.2.2 效率远高于纯Python代码

Numpy底层使用C语言编写，内部解除了GIL（全局解释器锁），其对数组的操作速度不受Python解释器的限制，所以，其效率远高于纯Python代码。

2.2.3 存储数据地址连续

ndarray在存储数据的时候，数据与数据的地址都是连续的，这样就使得批量操作数组元素时速度更快。

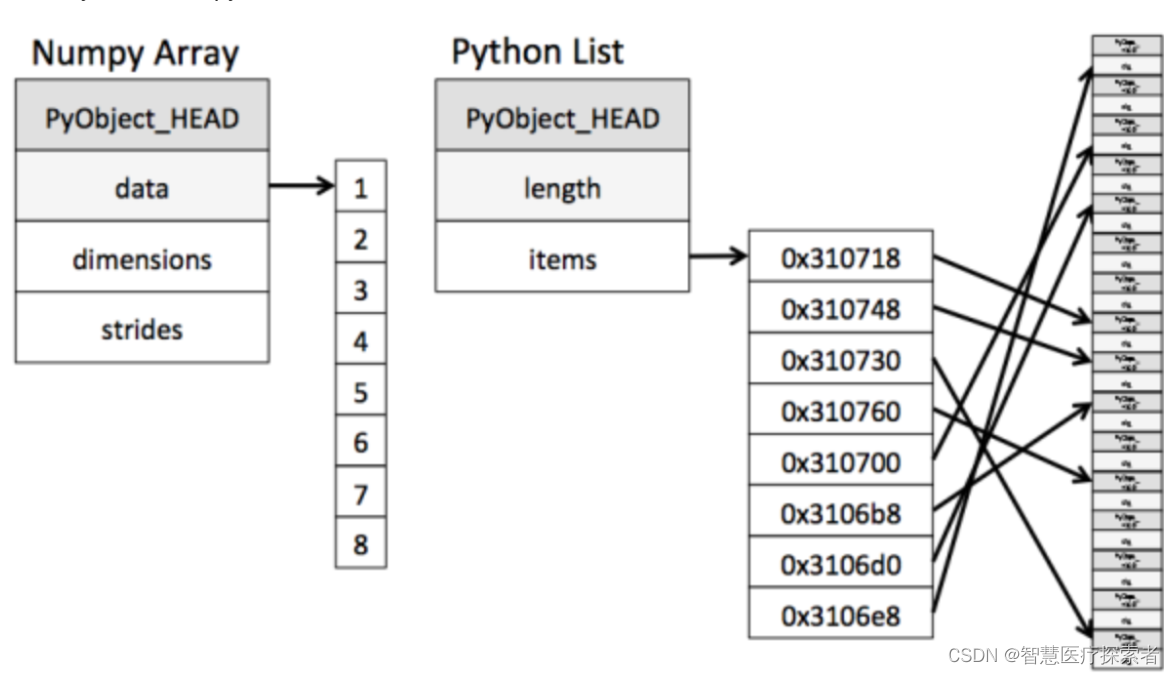
ndarray中的所有元素的类型都是相同的，而Python列表中的元素类型是任意的，所以ndarray在存储元素时内存可以连续，而python原生list就只能通过寻址方式找到下一个元素，这虽然也导致了在通用性能方面Numpy的ndarray不及Python原生list，但在科学计算中，Numpy的ndarray就可以省掉很多循环语句，代码使用方面比Python原生list简单的多。

2.3 如何创建Numpy对象

Numpy 定义了一个 n 维数组对象，简称 ndarray 对象，它是一个一系列相同类型元素组成的数组集合。数组中的每个元素都占有大小相同的内存块，使用索引或切片的方式可以获取数组中的每个元素。ndarray 对象有一个 dtype 属性，该属性用来描述元素的数据类型。ndarray 对象采用了数组的索引机制，将数组中的每个元素映射到内存块上，并且按照一定的布局对内存块进行排列，常用的布局方式有两种，即按行或者按列。

通过 Numpy 的内置函数 array() 可以创建 ndarray 对象，其语法格式如下：

numpy.array(object, dtype = None, copy = True, order = None,ndmin = 0)

2.3.1 使用Numpy创建ndarray数组

import numpy as np

a = np.array([1,2,3])
b = np.array([[1,2,3], [4,5,6]])

print(f'a:{a}')
print(f'type(a):{type(a)}')

print('b:{b}')

运行结果显示：

a:[1 2 3]
type(a):<class 'numpy.ndarray'>
b:{b}

2.3.2 查看数组维数并改变维度

import numpy as np

a = np.array([[1,2], [3,4], [5,6]])

print(a.ndim)
print("old array:", a)

a = a.reshape(2,3)
print("new array:", a.ndim, a)

运行结果显示：

old array: [[1 2]
 [3 4]
 [5 6]]
new array: 2 [[1 2 3]
 [4 5 6]]

2.3.3 通过ndarray的属性也可以操作数组

ndarray的属性

import numpy as np

a = np.array([[1,2], [3,4], [5,6]])
print('a.shape:', a.shape)
print('a:', a)
a.shape = (2, 3)
print('a[2,3]:', a)
print('a[3,2]:', a.reshape(3, 2))

print('a.ndim:', a.ndim)
print('a.itemsize:', a.itemsize)
print('a.flags:', a.flags)

a.shape: (3, 2)
a: [[1 2]
 [3 4]
 [5 6]]
a[2,3]: [[1 2 3]
 [4 5 6]]
a[3,2]: [[1 2]
 [3 4]
 [5 6]]
a.ndim: 2
a.itemsize: 4
a.flags:   C_CONTIGUOUS : True
  F_CONTIGUOUS : False
  OWNDATA : True
  WRITEABLE : True
  ALIGNED : True
  WRITEBACKIFCOPY : False

ndarray的类型

Numpy中的数据类型标识码，Numpy 中每种数据类型都有一个唯一标识的字符码，如下所示：

i - 整数
b - 布尔
u - 无符号整数
f - 浮点
c - 复合浮点数
m - timedelta
M - datetime
O - 对象
S - 字符串
U - unicode 字符串
V - 固定的其他类型的内存块 ( void )

通常，Numpy 与 SciPy 程序包一起使用，SciPy 可以看做对 Numpy 库的扩展，它在 Numpy 的基础上又增加了许多工程计算函数。

2.3.4 创建未初始化的数组

numpy.empty(shape, dtype = float, order = 'C')

numpy.empty() 创建未初始化的数组，可以指定创建数组的形状（shape）和数据类型（dtype）。

参数：

    shape：指定数组的形状；
    dtype：数组元素的数据类型，默认值是值 float；
    order：指数组元素在计算机内存中的储存顺序，默认顺序是“C”（“C”代表以行顺序存储，“F”则表示以列顺序存储）。

import numpy as np
n1 = np.empty([2, 2])
print(n1)

运行结果显示：

[[0.0e+000 5.4e-323]
 [9.9e-324 9.9e-324]]

2.3.4 创建元素均为 0 的数组

numpy.zeros(shape,dtype=float,order="C")

该函数用来创建元素均为 0 的数组，同时还可以指定被数组的形状。

参数：

    shape：指定数组的形状；
    dtype：数组元素的数据类型，默认值是值 float；
    order：指数组元素在计算机内存中的储存顺序，默认顺序是“C”（“C”代表以行顺序存储，“F”则表示以列顺序存储）。

import numpy as np
n1 = np.zeros([2, 2])
print(n1)

运行结果显示：

[[0. 0.]
 [0. 0.]]

2.3.4 创建1填充的指定形状大小与数据类型的新数组

numpy.ones(shape, dtype = None, order = 'C')

返回指定形状大小与数据类型的新数组，并且新数组中每项元素均用 1 填充。

import numpy as np
n1 = np.ones([2, 2])
print(n1)

运行结果显示

[[1. 1.]
 [1. 1.]]

2.3.5 将一个 Python 序列转化为 ndarray 对象

numpy.asarray（sequence，dtype = None ，order = None ）

asarray() 能够将一个 Python 序列转化为 ndarray 对象。

参数：

    sequence：接受一个 Python 序列，可以是列表或者元组；
    dtype：可选参数，数组的数据类型，默认值是值 float；
    order：指数组元素在计算机内存中的储存顺序，默认顺序是“C”（“C”代表以行顺序存储，“F”则表示以列顺序存储）。

import numpy as np


array = [1, 2, 3, 4, 5]
n1 = np.asarray(array)
print(n1)
print(type(n1))

运行结果显示

[1 2 3 4 5]
<class 'numpy.ndarray'>

2.3.6 使用指定的缓冲区创建数组

numpy.frombuffer(buffer, dtype = float, count = -1, offset = 0)

表示使用指定的缓冲区创建数组。

参数：

    buffer：将任意对象转换为流的形式读入缓冲区；
    dtype：返回数组的数据类型，默认是 float32；
    count：要读取的数据数量，默认为 -1 表示读取所有数据；
    offset：读取数据的起始位置，默认为 0。

import numpy as np

data =b'hello world!'
res = np.frombuffer(data,dtype='S3',offset=0)
print(res)

运行结果显示：

[b'hel' b'lo ' b'wor' b'ld!']

2.3.7 迭代对象转换为 ndarray 数组

numpy.fromiter(iterable, dtype, count = -1)

把迭代对象转换为 ndarray 数组，其返回值是一个一维数组。

参数：

    iterable：可迭代对象；
    dtype：数组元素的数据类型，默认值是值 float；
    count：读取的数据数量，默认为 -1，读取所有数据。

import numpy as np

iterable = (x * x*x for x in range(4))
n1 = np.fromiter(iterable, int)

print (n1)

运行结果显示

[ 0  1  8 27]

2.3.8 创建给定数值范围的数组

numpy.arange(start, stop, step, dtype)

参数：

    start： 起始值，默认是 0。
    stop： 终止值，注意生成的数组元素值不包含终止值。
    step： 步长，默认为 1。
    dtype： 可选参数，指定 ndarray 数组的数据类型。

import numpy as np

A = np.arange(5)
print(A)
print(type(A))

A = np.arange(1, 5)
print(A)

A = np.arange(1, 5, 2)
print(A)

A = np.arange(1, 5.2, 0.6)
print(A)

运行结果显示

[0 1 2 3 4]
<class 'numpy.ndarray'>
[1 2 3 4]
[1 3]
[1.  1.6 2.2 2.8 3.4 4.  4.6 5.2]

2.3.9 创建指定的数值区间内的数组

numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

参数：

    start：代表数值区间的起始值；
    stop：代表数值区间的终止值；
    num：表示数值区间内要生成多少个均匀的样本。默认值为 50；
    endpoint：默认为 True，表示数列包含 stop 终止值，反之不包含；
    retstep：默认为 True，表示生成的数组中会显示公差项，反之不显示；
    dtype：代表数组元素值的数据类型。

import numpy as np

n1 = np.linspace(start = 0, stop = 1, num = 11)
n2 = np.linspace(start = 0, stop = 100, num = 11)
n3 = np.linspace(start = 1, stop = 5, num = 4, endpoint = False)
n4 = np.linspace(start = 0, stop = 100, num = 5, dtype = int)
print(n1)
print(n2)
print(n3)
print(n4)

运行结果显示：

[0.  0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ]
[  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]
[1. 2. 3. 4.]
[  0  25  50  75 100]

2.3.10 创建等比数组

numpy.logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None)

参数：

    start： 序列的起始值：base**start。
    stop： 序列的终止值：base**stop。
    num： 数值范围区间内样本数量，默认为 50。
    endpoint： 默认为 True 包含终止值，反之不包含。
    base： 对数函数的 log 底数，默认为10。
    dtype： 可选参数，指定 ndarray 数组的数据类型。

logspace中，开始点和结束点是10的幂

import numpy as np

n1 = np.logspace(0,0,10)
n2 = np.logspace(0,9,10)
n3 = np.logspace(0,9,10,base=2)

print(n1)
print(n2)
print(n3)

运行结果显示：

[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1.e+00 1.e+01 1.e+02 1.e+03 1.e+04 1.e+05 1.e+06 1.e+07 1.e+08 1.e+09]
[  1.   2.   4.   8.  16.  32.  64. 128. 256. 512.]

2.4 Numpy运算

2.4.1 平铺数组元素

numpy.ndarray.flat()

返回一个数组迭代器，可以用 for 循环遍历其中的每一个元素。

import numpy as np

a = np.arange(8).reshape(2, 4)
print ('a:', a)

for e in a.flat:
    print (e, end=" ")

运行结果显示：

a: [[0 1 2 3]
 [4 5 6 7]]
0 1 2 3 4 5 6 7

2.4.2 以一维数组的形式返回一份数组副本

numpy.ndarray.flatten()

以一维数组的形式返回一份数组副本，对副本修改不会影响原始数组。

import numpy as np

a = np.arange(8).reshape(2, 4)
print(a)
print(a.flatten())

运行结果显示：

[[0 1 2 3]
 [4 5 6 7]]
[0 1 2 3 4 5 6 7]

2.4.2 转化成连续的扁平数组

numpy.ravel()

返回一个连续的扁平数组（即展开的一维数组），与 flatten不同，它返回的是数组视图（修改视图会影响原数组）。

import numpy as np

a1, a2 = np.mgrid[1:4:1, 2:3:1]
print("a1:\n", a1, "\n", "a2:\n", a2)

n1 = a1.ravel() 
n2 = a2.ravel()

print("n1:", n1)
print("n2:", n2)
sum = n1 + n2
print(sum)

运行结果显示：

a1:
 [[1]
 [2]
 [3]] 
 a2:
 [[2]
 [2]
 [2]]
n1: [1 2 3]
n2: [2 2 2]
[3 4 5]

2.4.3 Numpy 的位运算

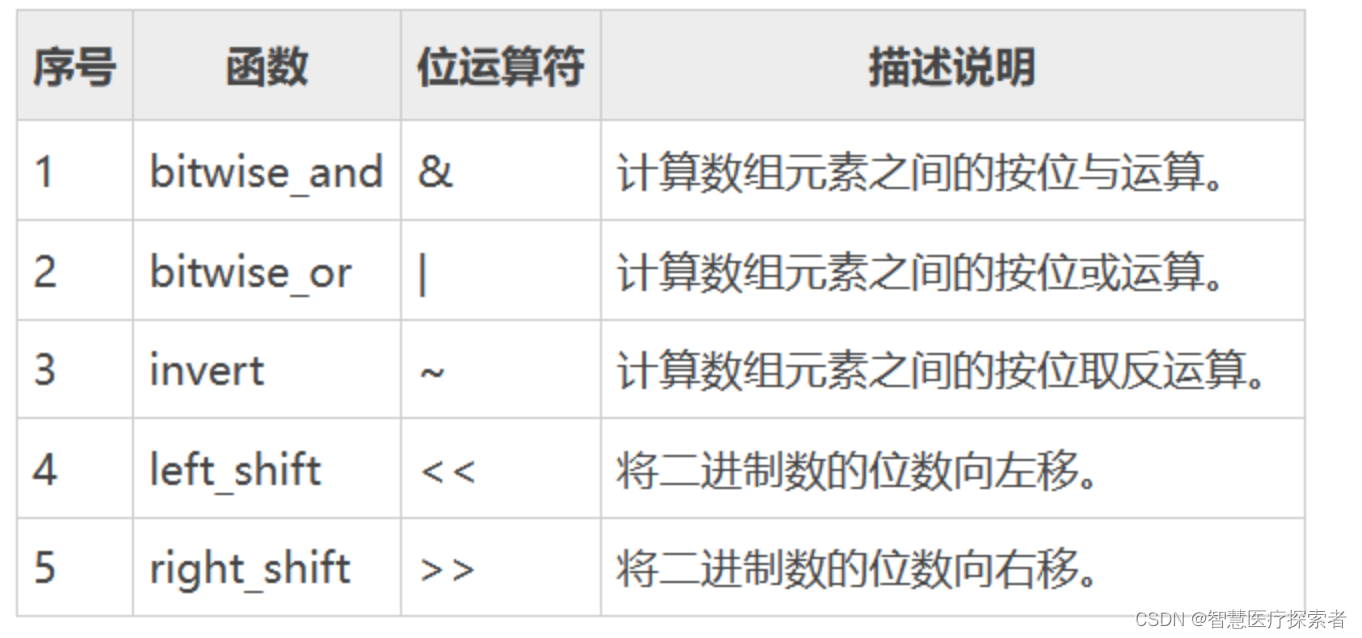
import numpy as np

n1 = np.bitwise_and([11,7], [4,25])
n2 = np.bitwise_and(np.array([2,5,255]), np.array([3,14,16]))
n3 = np.bitwise_and([True, True], [False, True])


n4 = np.bitwise_or([11,7], [4,25])
n5 = np.bitwise_or(np.array([2,5,255]), np.array([3,14,16]))
n6 = np.bitwise_or([True, True], [False, True])

print(n1)
print(n2)
print(n3)
print(n4)
print(n5)
print(n6)

运行结果显示：

[0 1]
[ 2  4 16]
[False  True]
[15 31]
[  3  15 255]
[ True  True]

2.4.4 算术运算

NumPy 数组的“加减乘除”算术运算，分别对应 add()、subtract()、multiple() 以及 divide() 函数。

numpy.reciprocal()函数对数组中的每个元素取倒数，并以数组的形式将它们返回。
numpy.power()将 a 数组中的元素作为底数，把 b 数组中与 a 相对应的元素作幂，最后以数组形式返回两者的计算结果。
numpy.mod()返回两个数组相对应位置上元素相除后的余数

import numpy as np

a = np.random.randint(9, size=(3, 3))
print("a =", a)
b = np.random.randint(9, size=(3, 3))
print("b =", b)
print("a + b =", np.add(a, b))
print("a - b =", np.subtract(a, b))
print("a x b =", np.multiply(a, b))
print("a / b =", np.divide(a, b))

运行结果显示：

a = [[8 0 2]
 [7 8 4]
 [3 5 1]]
b = [[2 3 5]
 [1 8 3]
 [4 1 2]]
a + b = [[10  3  7]
 [ 8 16  7]
 [ 7  6  3]]
a - b = [[ 6 -3 -3]
 [ 6  0  1]
 [-1  4 -1]]
a x b = [[16  0 10]
 [ 7 64 12]
 [12  5  2]]
a / b = [[4.         0.         0.4       ]
 [7.         1.         1.33333333]
 [0.75       5.         0.5       ]]

2.4.5 Numpy矩阵操作

NumPy 提供了一个矩阵库模块numpy.matlib，该模块中的函数返回的是一个 matrix 对象，而非 ndarray 对象。矩阵由 m 行 n 列（m*n）元素排列而成，矩阵中的元素可以是数字、符号或数学公式等。

numpy.matlib.empty() 返回一个空矩阵，它的创建速度非常快。
numpy.matlib.zeros() 创建一个以 0 填充的矩阵。
numpy.matlib.ones() 创建一个以 1 填充的矩阵。
numpy.matlib.eye() 返回一个对角线元素为 1，而其他元素为 0 的矩阵。
numpy.matlib.identity()该函数返回一个给定大小的单位矩阵，矩阵的对角线元素为 1，而其他元素均为 0。
numpy.matlib.rand() 创建一个以随机数填充，并给定维度的矩阵。

import numpy as np
import numpy.matlib

print(np.matlib.empty((3, 4)))
print(np.matlib.zeros((3, 4)))
print(np.matlib.ones((3, 4)))

运行结果显示：

[[0.00000000e+000             nan 1.69759663e-313 0.00000000e+000]
 [0.00000000e+000 0.00000000e+000 0.00000000e+000 0.00000000e+000]
 [0.00000000e+000 0.00000000e+000 0.00000000e+000 0.00000000e+000]]
[[0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]]
[[1. 1. 1. 1.]
 [1. 1. 1. 1.]
 [1. 1. 1. 1.]]

2.4.5 两个矩阵的逐元素乘法

multiple()

函数用于两个矩阵的逐元素乘法。

import numpy as np

a1=np.array([[1,2], [3,4]], ndmin=2)
a2=np.array([[1,2], [3,4]], ndmin=2)

print(np.multiply(a1, a2))

[[ 1  4]
 [ 9 16]]

2.4.6 两个数组的矩阵乘积

matmul()
用于计算两个数组的矩阵乘积。

import numpy as np

a1=np.array([[1,2], [3,4]], ndmin=2)
a2=np.array([[1,2], [3,4]], ndmin=2)

print(np.matmul(a1, a2))

运行结果显示：

[[ 7 10]
 [15 22]]

2.4.7 两个矩阵的点积

dot()
函数用于计算两个矩阵的点积。

import numpy as np

a1=np.array([[1,2], [3,4]], ndmin=2)
a2=np.array([[1,2], [3,4]], ndmin=2)

print(np.dot(a1, a2))

[[ 7 10]
 [15 22]]

2.4.8 两个矩阵内积

numpy.inner()
用于计算数组之间的内积。

import numpy as np
n1=np.inner(np.array([1,2,3,4]),np.array([1,2,3,4]))
a1=np.array(([[1,2],[3,4]]))
a2=np.array(([[11,12],[13,14]]))
n2=np.inner(a1,a2)

print(n1)
print(n2)

运行结果显示：

30
[[35 41]
 [81 95]]

2.4.9 解线性矩阵方程

numpy.linalg.solve()
该函数用于求解线性矩阵方程组，并以矩阵的形式表示线性方程的解。

解方程组x0 + 2 * x1 = 1和3 * x0 + 5 * x1 = 2:

import numpy as np

a = np.array([[1, 2], [3, 5]])
b = np.array([1, 2])
x = np.linalg.solve(a, b)
print(x)

运行结果显示：

[-1.  1.]

2.4.10 计算矩阵的逆矩阵

numpy.linalg.inv()
该函数用于计算矩阵的逆矩阵，逆矩阵与原矩阵相乘得到单位矩阵。

import numpy as np

a = np.array([[[1., 2.], [3., 4.]], [[1, 3], [3, 5]]])
n =np.linalg.inv(a)
print(a)
print(n)

运行结果显示：

[[[1. 2.]
  [3. 4.]]

 [[1. 3.]
  [3. 5.]]]
[[[-2.    1.  ]
  [ 1.5  -0.5 ]]

 [[-1.25  0.75]
  [ 0.75 -0.25]]]
[[[-2.    2.  ]
  [ 4.5  -2.  ]]

 [[-1.25  2.25]
  [ 2.25 -1.25]]]

3 Tensor和Numpy的相互转换

3.1 Tensor转Numpy

import numpy as np
import torch

t = torch.arange(1, 10).reshape(3, 3)
x = t.numpy()
print(f'a={t}')
print(f'b={x}')

运行结果显示：

a=tensor([[1, 2, 3],
          [4, 5, 6],
          [7, 8, 9]])
b=[[1 2 3]
   [4 5 6]
   [7 8 9]]

3.2 Numpy转Tensor

3.2.1 使用torch.tensor

import numpy as np
import torch
a = np.random.normal(0, 1, (2, 3))
b = torch.tensor(a)
print(f'a={a}, b={b}')

运行结果显示：

a=[[ 1.77128009  2.02509013  0.38144148]
   [ 1.14920329 -0.30733646 -1.20198951]]
b=tensor([[ 1.7713,  2.0251,  0.3814],
          [ 1.1492, -0.3073, -1.2020]], dtype=torch.float64)

3.2.2 使用torch.from_numpy

import numpy as np
import torch

a = np.random.normal(0, 1, (4, 5))
b = torch.from_numpy(a)
print(f'a={a}')
print(f'b={b}')

运行结果显示：

a=[[ 1.27357033  0.43722359 -0.74243293 -0.19531152  0.95053336]
   [-0.52235811  0.95262418 -0.11157708  0.65592213  0.04188334]
   [ 0.14932165 -0.40966126  0.09067062  0.3212764  -2.41411188]
   [ 0.63391603  0.29742247 -0.43064322  1.08767221 -0.95699876]]
b=tensor([[ 1.2736,  0.4372, -0.7424, -0.1953,  0.9505],
          [-0.5224,  0.9526, -0.1116,  0.6559,  0.0419],
          [ 0.1493, -0.4097,  0.0907,  0.3213, -2.4141],
          [ 0.6339,  0.2974, -0.4306,  1.0877, -0.9570]], dtype=torch.float64)

4 Tensor转其他

4.1 Tensor转数值

import torch

a = torch.tensor([1])
b = a.item()

print(f'a={a}')
print(f'b={b}')

运行结果显示：

a=tensor([1])
b=1

4.2 Tensor转List

import torch

t1 = torch.arange(10)
t2 = t1.tolist() 

print(f't1={t1}')
print(f't2={t2}')

运行结果显示：

t1=tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
t2=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

4.3 Tensor转List Tensor

import torch

t1 = torch.arange(10)
t3 = list(t1)

print(f't1={t1}')
print(f't3={t3}')

运行结果显示

t1=tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
t3=[tensor(0), tensor(1), tensor(2), tensor(3), tensor(4), tensor(5), tensor(6), tensor(7), tensor(8), tensor(9)]