文章目录
- 1. JZ31 栈的压入、弹出序列
- 辅助栈
- 原地栈 数组模拟
- 2. JZ32 从上往下打印二叉树
- 迭代
- 递归
- 3. JZ33 二叉搜索树的后序遍历序列
- 递归
- 迭代 递增栈
- 4. JZ34 二叉树中和为某一值的路径(二)
- 5. JZ35 复杂链表的复制
- 6. JZ36 二叉搜索树与双向链表
- 递归
- 迭代
- 7. JZ38 字符串的排列
- next_permutation
- DFS+回溯算法
- 8. JZ39 数组中出现次数超过一半的数字
- 哈希表
- 摩尔投票法
- 9. JZ40 最小的K个数
- 堆排序 大顶堆 优先队列
- 堆排序 小顶堆 vector
- 10. JZ42 连续子数组的最大和
- 动态规划
- 动态规划 空间优化
- 补充内容
- next_permutation
- 堆排序
1. JZ31 栈的压入、弹出序列
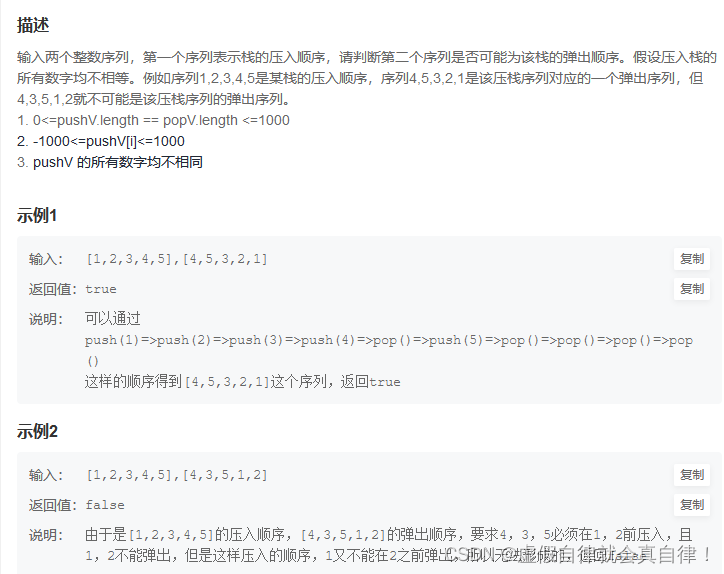
辅助栈
思路一样,刚开始写的时候for循环内的while写成了if,两层循环,时间、空间复杂度:O(n)
#include <iterator>
class Solution {
public:
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
//栈
//有一个栈为空都不能完成出入栈
if(pushV.empty() || popV.empty() || pushV.size() != popV.size()) return false;
stack<int> st;
int cur = 0;
for(int i=0; i<pushV.size(); i++)
{
st.push(pushV[i]);//先存入数据
//判断栈顶元素与出栈序列的值是否相等 while 要保证栈内有元素
while(!st.empty() && st.top() == popV[cur])
{
st.pop();
cur++;
}
}
return st.empty() ? true : false; //return st.size() == 0 ? true : false;
}
};
原地栈 数组模拟
在辅助栈的做法中,push数组前半部分入栈了,就没用了,这部分空间我们就可以用来当成栈。而且数组本身就类似栈,用下标表示栈顶。原理一样,只是这时遍历push数组时,用下标n表示栈空间,n的位置就是栈顶元素。这个做法很巧妙

#include <iterator>
class Solution {
public:
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
//有一个栈为空都不能完成出入栈
if(pushV.empty() || popV.empty() || pushV.size() != popV.size()) return false;
//原地栈 数组模拟
int n = 0;//表示栈空间的大小,初始化为0
int cur = 0;//出栈序列的下标
for(auto num : pushV)
{
pushV[n] = num;//相当于存入数据
while(n >= 0 && pushV[n] == popV[cur])//当栈不为空且栈顶等于当前出栈序列
{
n--;//逻辑出栈 缩小栈空间 让该位置在下一轮被替换成新的元素
cur++;
}
n++;//入栈
}
return n==0;//最后的栈是否为空
}
};
2. JZ32 从上往下打印二叉树
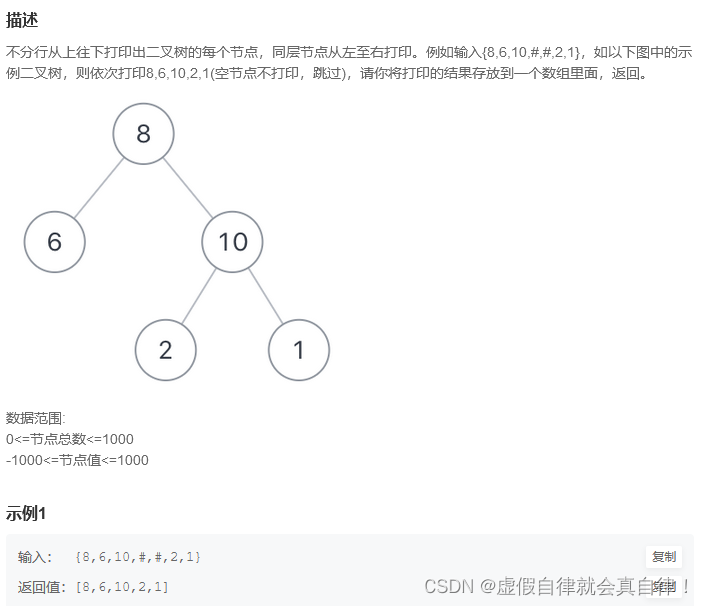
迭代
前序遍历+队列+迭代
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
vector<int> PrintFromTopToBottom(TreeNode* root) {
vector<int> result;
if(root == nullptr) return result;
//队列实现
queue<TreeNode*> que;
que.push(root);
TreeNode* cur = nullptr;
while(!que.empty())
{
cur = que.front();
que.pop();
result.push_back(cur->val);
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
return result;
}
};
递归

/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
#include <vector>
class Solution {
public:
vector<int> PrintFromTopToBottom(TreeNode* root) {
vector<int> result;
if(root == nullptr) return result;
//递归
vector<vector<int>> temp;
traverse(root, temp, 1);
//送入一维数组
for(int i=0; i<temp.size(); i++)
{
for(int j=0; j<temp[i].size(); j++)
result.push_back(temp[i][j]);
}
return result;
}
void traverse(TreeNode* root, vector<vector<int>>& result, int depth)
{
if(root == nullptr) return;
else{
if(result.size() < depth) result.push_back(vector<int>{});
result[depth-1].push_back(root->val);
}
traverse(root->left, result, depth + 1);
traverse(root->right, result, depth + 1);
}
};
3. JZ33 二叉搜索树的后序遍历序列
题目: 从上往下打印出二叉树的每个节点,同层节点从左至右打印。要求:空间复杂度 O(n),时间时间复杂度 O(n^2)
提示:
1.二叉搜索树是指父亲节点大于左子树中的全部节点,但是小于右子树中的全部节点的树。
2.该题我们约定空树不是二叉搜索树
3.后序遍历是指按照 “左子树-右子树-根节点” 的顺序遍历
递归
递归写法就是找到根节点,根节点作为分割点,两边判断大小
class Solution {
public:
bool VerifySquenceOfBST(vector<int> sequence) {
if(sequence.empty()) return false;
if(sequence.size() == 1) return true;
return isBST(sequence, 0, sequence.size()-1);
}
bool isBST(vector<int>& sequence, int left, int right)
{
if(left >= right) return true;//递归结束
int low = left;
//判断左子节点和根节点 并找到右子结点位置 此时为low
while(low <= right && sequence[low] < sequence[right]) ++low;
//判断右子节点和根节点
for(int i=low; i<right; i++)
{
if(sequence[i] <= sequence[right]) return false;
}
//此时左子树起始区间是left low-1;右子树起始区间是low right-1
return isBST(sequence, left, low-1) && isBST(sequence, low, right-1);//下一轮更新 递归
}
};
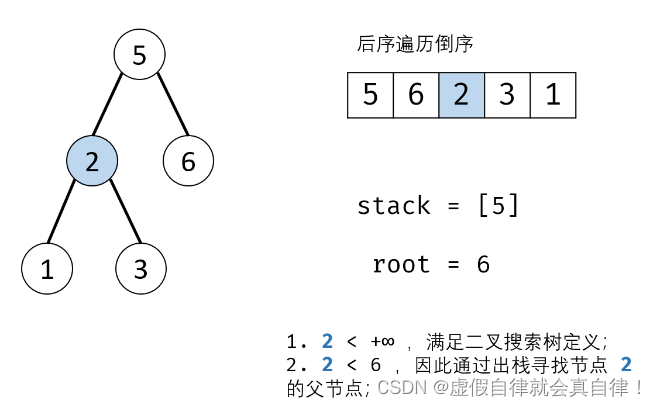
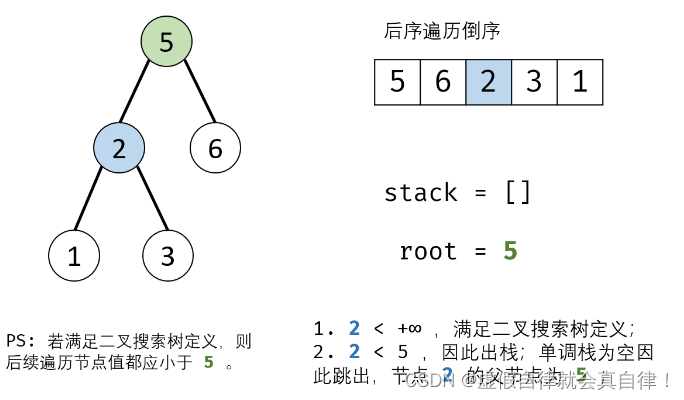
迭代 递增栈
后序遍历的倒序=先序遍历的镜像 根右左
while循环主要是找到当前序列访问值的父结点,如下:
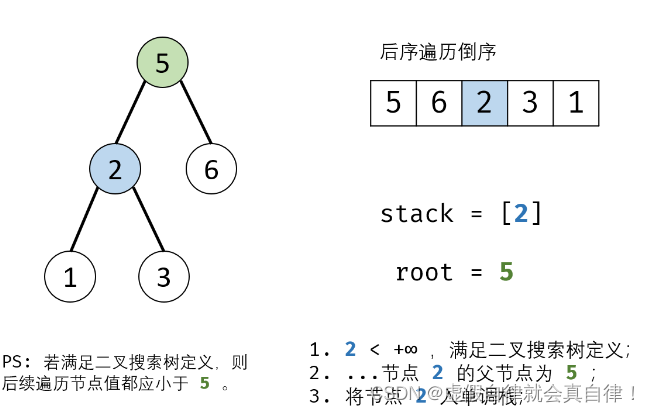
#include <climits>
class Solution {
public:
bool VerifySquenceOfBST(vector<int> sequence) {
if(sequence.empty()) return false;
if(sequence.size() == 1) return true;
//递归
//return isBST(sequence, 0, sequence.size()-1);
//迭代 单调栈
int cur = INT_MAX;
stack<int> st;
// 后序遍历的倒序=先序遍历镜像 根右左
//二叉搜索树:左 < 根 < 右
for(int i=sequence.size()-1; i>=0; i--)
{
if(sequence[i] > cur) return false;
//保证栈非空状态下访问栈顶元素 找到sequence[i]的父节点 用while
while(!st.empty() && sequence[i] < st.top())//sequence[i]为左结点
{
cur = st.top();//这个才是当前sequence[i]的父结点
st.pop();
}
st.push(sequence[i]);
}
return true;
}
//递归
bool isBST(vector<int>& sequence, int left, int right)
{
if(left >= right) return true;//递归结束
int low = left;
//判断左子节点和根节点 并找到右子结点位置 此时为low
while(low <= right && sequence[low] < sequence[right]) ++low;
//判断右子节点和根节点
for(int i=low; i<right; i++)
{
if(sequence[i] <= sequence[right]) return false;
}
//此时左子树起始区间是left low-1;右子树起始区间是low right-1
return isBST(sequence, left, low-1) && isBST(sequence, low, right-1);//下一轮更新 递归
}
};
4. JZ34 二叉树中和为某一值的路径(二)
题目:输入一颗二叉树的根节点和一个整数,按字典序打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
递归+回溯
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
vector<vector<int> > FindPath(TreeNode* root, int target) {
v.clear();
result.clear();
v.push_back(root->val);
isPath(root, target - root->val);//中结点
return result;
}
void isPath(TreeNode* root, int target)
{
//遍历到叶子结点 且值为0
if(root->left == nullptr && root->right == nullptr && target == 0)
{
result.push_back(v);
return;
}
if(root->left)
{
v.push_back(root->left->val);//保存当前节点值
target -= root->left->val;
isPath(root->left, target);//递归
target += root->left->val;//回溯
v.pop_back();
}
if(root->right)
{
v.push_back(root->right->val);
target -= root->right->val;
isPath(root->right, target);
target += root->right->val;
v.pop_back();
}
return;
}
private:
vector<int> v;
vector<vector<int>> result;
};
5. JZ35 复杂链表的复制
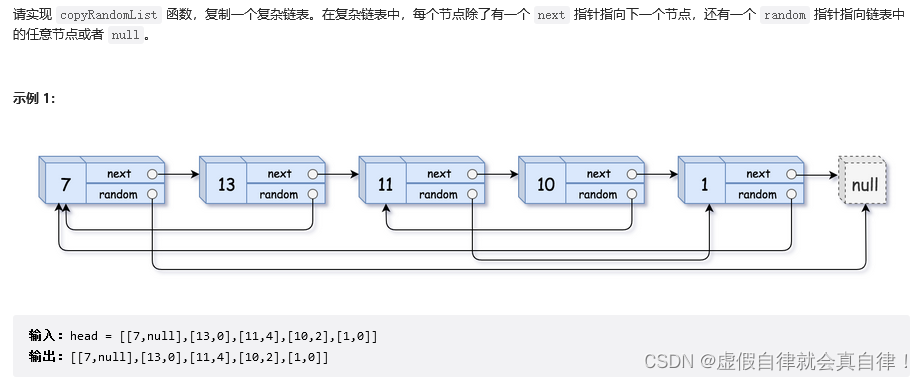 好难呀,又来搬运力扣大佬Krahets的解法了
好难呀,又来搬运力扣大佬Krahets的解法了
1. 链表的定义
// 普通链表的节点定义如下:
class Node {
public:
int val;
Node* next;
Node(int _val) {
val = _val;
next = NULL;
}
};
// 本题链表的节点定义如下:
class Node {
public:
int val;
Node* next;
Node* random;
Node(int _val) {
val = _val;
next = NULL;
random = NULL;
}
};
2. 题目难点
给定链表的头节点 head ,复制普通链表只需遍历链表,每轮建立新节点 + 构建前驱节点 pre 和当前节点 node 的引用指向即可。
本题链表的节点新增了 random 指针,指向链表中的 任意节点 或者 null 。这个 random 指针意味着在复制过程中,除了构建前驱节点和当前节点的引用指向 pre.next ,还要构建前驱节点和其随机节点的引用指向 pre.random 。
本题难点: 在复制链表的过程中构建新链表各节点的 random 引用指向。

3. 思路
class Solution {
public:
Node* copyRandomList(Node* head) {
Node* cur = head;
Node* dum = new Node(0), *pre = dum;
while(cur != nullptr) {
Node* node = new Node(cur->val); // 复制节点 cur
pre->next = node; // 新链表的 前驱节点 -> 当前节点
// pre->random = "???"; // 新链表的 「 前驱节点 -> 当前节点 」 无法确定
cur = cur->next; // 遍历下一节点
pre = node; // 保存当前新节点
}
return dum->next;
}
};
4. 哈希表 迭代写法

/*
struct RandomListNode {
int label;
struct RandomListNode *next, *random;
RandomListNode(int x) :
label(x), next(NULL), random(NULL) {
}
};
*/
class Solution {
public:
RandomListNode* Clone(RandomListNode* pHead) {
//哈希表
if(pHead == nullptr) return nullptr;
unordered_map<RandomListNode*, RandomListNode*> hashmap;//原结点 复制的新结点
RandomListNode* cur = pHead;
//1. 复制各节点,并建立 “原节点 -> 新节点” 的 Map 映射 建立值映射
for(RandomListNode* p = cur; p != nullptr; p = p->next)
{
hashmap[p] = new RandomListNode(p->label);
}
//2. 构建新链表的 next 和 random 指向 建立指向映射
while(cur!=nullptr)
{
//新结点hashmap[cur]的 指向 hashmap[cur]->next 就是 原结点cur的指向 cur->next
hashmap[cur]->next = hashmap[cur->next];
hashmap[cur]->random = hashmap[cur->random];
cur = cur->next;
}
return hashmap[pHead];
}
};
5. 哈希表 递归写法
/*
struct RandomListNode {
int label;
struct RandomListNode *next, *random;
RandomListNode(int x) :
label(x), next(NULL), random(NULL) {
}
};
*/
class Solution {
public:
RandomListNode* Clone(RandomListNode* pHead) {
//2. 哈希表 递归
if(pHead == nullptr) return nullptr;
RandomListNode* newhead = new RandomListNode(pHead->label);//复制头结点
hashmap[newhead] = pHead;//“原节点 -> 新节点” 的 Map 映射 值映射
newhead->next = Clone(pHead->next);//next指向
if(pHead->random != nullptr) newhead->random = Clone(pHead->random);//如果有random指向
return hashmap[newhead];
}
private:
unordered_map<RandomListNode*, RandomListNode*> hashmap;//原结点 复制的新结点
};
6. 拼接 + 拆分 原地解法

/*
struct RandomListNode {
int label;
struct RandomListNode *next, *random;
RandomListNode(int x) :
label(x), next(NULL), random(NULL) {
}
};
*/
class Solution {
public:
RandomListNode* Clone(RandomListNode* pHead) {
if(pHead == nullptr) return nullptr;
//3. 拼接 + 拆分 原地解法
RandomListNode* cur = pHead;
//复制结点及next指向
while(cur != nullptr)
{
RandomListNode* temp = new RandomListNode(cur->label);//复制结点 新结点
temp->next = cur->next;// 新结点 -> 原下一个结点
cur->next = temp;// 原结点 -> 新结点
cur = temp->next;//cur = cur->next->next;//cur更新为 原结点的下一个结点
}
//复制结点的random指向
cur = pHead;
while (cur != nullptr)
{
//新结点cur->next 的random指向 = 原结点cur 的random指向
if(cur->random != nullptr) cur->next->random = cur->random->next;
cur = cur->next->next;//更新cur
}
//分离链表
cur = pHead->next;//新结点表头
RandomListNode* old = pHead, *result = pHead->next;
while(cur->next != nullptr)
{
old->next = old->next->next;//分离
cur->next = cur->next->next;
old = old->next;//更新
cur = cur->next;
}
old->next = nullptr;// 单独处理原链表尾节点
return result;
}
};
6. JZ36 二叉搜索树与双向链表
题目描述:输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
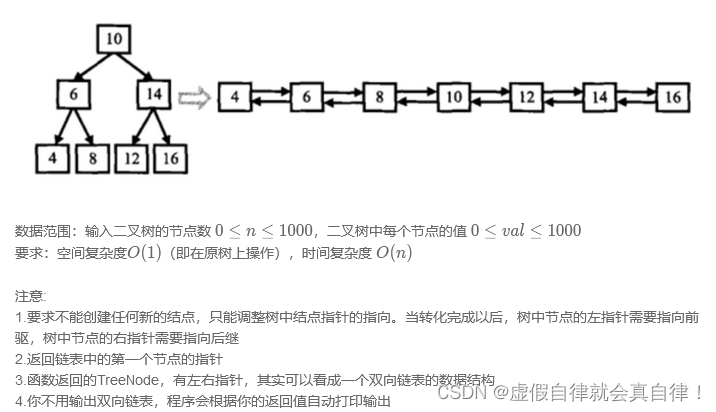
递归
- vector
/*
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
#include <vector>
class Solution {
public:
TreeNode* Convert(TreeNode* pRootOfTree)
{
if (pRootOfTree == nullptr) return pRootOfTree;
//1. vector保存结点,递归实现
treeTovector(pRootOfTree, result);
return doublyList(result);
}
private:
vector<TreeNode*> result;
void treeTovector(TreeNode* root, vector<TreeNode*>& result)
{
if(root == nullptr) return;
treeTovector(root->left, result);
result.push_back(root);
treeTovector(root->right, result);
}
TreeNode* doublyList(vector<TreeNode*>& result) {
for (int i = 0; i < result.size()-1; ++i) {
result[i]->right = result[i + 1];
result[i+1]->left = result[i];
}
return result[0];
}
};
- 仅递归 原地操作
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
#include <vector>
class Solution {
public:
TreeNode* Convert(TreeNode* pRootOfTree)
{
if (pRootOfTree == nullptr) return pRootOfTree;
//4. 递归
if(pRootOfTree == nullptr) return nullptr;//递归结束
Convert(pRootOfTree->left);//首先递归到最左最小值
if(pre == nullptr)//找到最小值,初始化head与pre
{
head = pRootOfTree;
pre = pRootOfTree;
}
else
{
pre->right = pRootOfTree;//建立连接
pRootOfTree->left = pre;//建立连接
pre = pRootOfTree;//结点更新
}
Convert(pRootOfTree->right);//处理右子树
return head;
}
private:
TreeNode* pre = nullptr;//指向当前遍历的前一节点
TreeNode* head = nullptr;//表头
};
迭代
- stack+vector
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
#include <vector>
class Solution {
public:
TreeNode* Convert(TreeNode* pRootOfTree)
{
if (pRootOfTree == nullptr) return pRootOfTree;
//2. stack+vector,迭代实现
while(!st.empty() || pRootOfTree != nullptr)
{
if(pRootOfTree != nullptr)
{
st.push(pRootOfTree);//入栈顺序是中左
pRootOfTree = pRootOfTree->left;
}
else
{
pRootOfTree = st.top();
result.push_back(pRootOfTree);//出栈顺序是左中
st.pop();
pRootOfTree = pRootOfTree->right;//右入栈 出栈
}
}
return doublyList(result);
}
private:
vector<TreeNode*> result;
stack<TreeNode*> st;
TreeNode* doublyList(vector<TreeNode*>& result) {
for (int i = 0; i < result.size()-1; ++i) {
result[i]->right = result[i + 1];
result[i+1]->left = result[i];
}
return result[0];
}
};
- stack
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
#include <vector>
class Solution {
public:
TreeNode* Convert(TreeNode* pRootOfTree)
{
if (pRootOfTree == nullptr) return pRootOfTree;
//3. 栈 迭代
//栈为空说明遍历结束
while(pRootOfTree != nullptr || !st.empty())
{
while(pRootOfTree != nullptr)//找到树的最左叶子 最左值 表头
{
st.push(pRootOfTree);
pRootOfTree = pRootOfTree->left;
}
if(!st.empty())
{
pRootOfTree = st.top();//树的最左叶子 最左值
st.pop();
if(pre == nullptr)//此时第一次出栈 将第一个出栈的结点设置为表头 最左值
{
head = pRootOfTree;//记录下最小的元素
}
else //建立新连接 双向连接
{
pre->right = pRootOfTree;//建立新连接
pRootOfTree->left = pre;
}
//结点更新
pre = pRootOfTree;//pre设置为当前值
pRootOfTree = pRootOfTree->right;//pRootOfTree设置为下一个遍历节点
}
}
return head;
}
private:
TreeNode* pre = nullptr;//指向当前遍历的前一节点
TreeNode* head = nullptr;//表头
stack<TreeNode*> st;
7. JZ38 字符串的排列
题目描述:输入一个字符串,长度不超过9(可能有字符重复),字符只包括大小写字母。
next_permutation
返回全排列,必须要进行排序才可以,使用方法如下所示
#include <algorithm>
class Solution {
public:
vector<string> Permutation(string str) {
//next_permutation
if(str.size() == 0) return vector<string>();
sort(str.begin(), str.end());
do {
result.push_back(str);
}while (next_permutation(str.begin(), str.end()));
return result;
}
vector<string> result;
};
DFS+回溯算法
每一层:从头开始遍历字符串,每次交换一个字符,遍历到末尾结束,每找到一个排列就保存;
每层递归后要回溯;
有可能有重复的,要去重,可以用set,也可以用map标记哪个字符使用过;
最后返回时,vector要排序,set不用
#include <algorithm>
#include <vector>
class Solution {
public:
vector<string> Permutation(string str) {
if(str.size() == 0) return vector<string>();
//dfs
dfs(str, 0, str.size()-1);
sort(result.begin(), result.end());
return result;
}
vector<string> result;
void dfs(string& s, int start, int end)
{
if(start == end)
{
result.push_back(s);
return;
}
unordered_map<int, int> visited;
for(int i=start; i<=end; ++i)
{
if(visited[s[i]] == 1) continue;//该元素使用 不能再用
swap(s[i], s[start]);
dfs(s, start+1, end);//递归
swap(s[i], s[start]);//回溯
visited[s[i]] = 1;//标记s[i]使用过
}
}
};
8. JZ39 数组中出现次数超过一半的数字

哈希表
时间复杂度 O(n),空间复杂度O(n)
class Solution {
public:
int jumpFloor(int number) {
//动态规划
if(number == 1) return 1;
if(number == 2) return 2;
vector<int> dp(3);
dp[0] = 1;
dp[1] = 2;
for(int i=2; i<number; i++)
{
dp[i % 2] = dp[(i-1) % 2] + dp[(i-2) % 2];
}
return dp[(number-1) % 2];
}
};
摩尔投票法
摩尔投票法,成立前提就是有出现超过一半的元素,所以最后我们需要判断找到的元素是否出现超过一半了。时间复杂度 O(n),空间复杂度O(1)
做法:
- 维护一个候选众数candidate 和它的投票数count。初始时candidate 可以为任意值,count为0;
- 遍历数组,先看投票数,再看当前值 x 与候选众数是否相等:
- 如果投票数 count 为 0,表示没有候选人,选取当前数x 为候选人,count设置为1(也可以统计投票数,即count++)
- 如果投票数 count > 0,看当前值 x 与候选众数是否相等:
- 如果 x 与 candidate 相等,那么 count 加 1;
- 如果 x 与 candidate 不等,那么 count 减少 1。
- 遍历完后,candidate 即为整个数组的众数,再统计其投票数即可
class Solution {
public:
int MoreThanHalfNum_Solution(vector<int>& numbers) {
//摩尔投票法的变种
int cnt = 0, candidate = 0;
for(const int n : numbers)
{
if(cnt == 0)//没有候选人
{
candidate = n;
cnt = 1;//count++;
}
else {
candidate == n ? cnt++ : cnt--;
}
}
//统计众数频率
cnt = std::count(numbers.begin(), numbers.end(), candidate);
/*
cnt = 0;
for(const int k : numbers)
{
if(k == candidate) cnt++;
}
*/
return cnt > numbers.size() / 2 ? candidate : 0;
}
};
9. JZ40 最小的K个数
题目描述:输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4。要求:空间复杂度 O(n) ,时间复杂度 O(nlogk)
堆排序 大顶堆 优先队列
 建立一个容量为k的大根堆的优先队列。遍历一遍元素,如果队列大小<k,就直接入队,否则,让当前元素与队顶元素相比,如果队顶元素大,则出队,将当前元素入队。
建立一个容量为k的大根堆的优先队列。遍历一遍元素,如果队列大小<k,就直接入队,否则,让当前元素与队顶元素相比,如果队顶元素大,则出队,将当前元素入队。
时间复杂度:O(nlongk), 插入容量为k的大根堆时间复杂度为O(longk), 一共遍历n个元素。空间复杂度:O(k)
- 写法1
#include <queue>
class Solution {
public:
vector<int> result;
vector<int> GetLeastNumbers_Solution(vector<int>& input, int k) {
if(k == 0 || input.size() == 0) return result;
//堆排序 写法1
priority_queue<int> pq;
//构建一个k个大小的堆
for(int i=0; i<k; i++)
pq.push(input[i]);
for(int i=k; i<input.size(); i++)
{
//较小元素入堆
if(pq.top() > input[i])
{
pq.pop();
pq.push(input[i]);
}
}
//堆中元素取出入vector
for(int i=0; i<k; i++)
{
result.push_back(pq.top());
pq.pop();
}
sort(result.begin(), result.end());//最后返回结果要排序 可以在创建优先队列时加入greater<int>关键字
return result;
}
};
- 写法2
#include <queue>
class Solution {
public:
vector<int> result;
vector<int> GetLeastNumbers_Solution(vector<int>& input, int k) {
if(k == 0 || input.size() == 0) return result;
//堆排序 写法2
priority_queue<int, vector<int>, greater<int>> pq;
//所有元素按照升序入队列
for(auto i : input)
pq.push(i);
//取出前k个元素
while(k--)
{
result.push_back(pq.top());
pq.pop();
}
return result;
}
};
堆排序 小顶堆 vector
#include <queue>
#include <vector>
class Solution {
public:
vector<int> result;
vector<int> GetLeastNumbers_Solution(vector<int>& input, int k) {
if(k == 0 || input.size() == 0) return result;
//堆排序 写法3
myTopk(input, input.size(), k);
return result;
}
void buildHeap(vector<int>& array, int len)
{
int lastNodeindex = array.size()-1;//结点总数
//最后一个非叶子就是第lastNodeindex /2 个
//从一棵树的最后一个非叶子节点开始建立堆
int root = (lastNodeindex-1) >> 1;//等价于(lastNodeindex - 1)/2
for(int i=root; i>=0; --i)
heapify(array, len, i);
}
//对一颗完全二叉树的指定非叶子节点及其叶子结点进行堆的建立
void heapify(vector<int>& array, int len, int i)
{
//如果i>=len,证明数组中的元素都已经建立成小根堆了,递归终止
if(i >= len) return;
int left = 2 * i + 1; //左孩子节点的下标
int right = 2 * i + 2; //右孩子节点的下标
int min = i; //默认数值最小的节点为该非叶子节点的值
//判断左孩子节点是否在索引范围内及左孩子结点值是否小于根节点,小于的话就将较大值的下标记录在min中
if(left < len && array[left] < array[min]) min = left;
if(right < len && array[right] < array[min]) min = right;
if(min != i)
{
swap(array[i], array[min]);//如果最小值的下标改变,则需要交换两个下标所对应的值
heapify(array, len, min); //对剩下的不是完全二叉树的元素继续进行堆的建立
}
}
void myTopk(vector<int>& array, int len, int k)
{
buildHeap(array, len);
for(int i=len-1; i>=0 && k; --i)
{
swap(array[i], array[0]);
result.push_back(array[i]);
--k;
heapify(array, i, 0);
}
}
};
10. JZ42 连续子数组的最大和

动态规划
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int>& array) {
//动态规划
vector<int> dp(array.size(), 0);
dp[0] = array[0];
int result = dp[0];
for(int i=1; i<array.size(); i++)
{
dp[i] = max(dp[i-1]+array[i], array[i]);
result = max(result, dp[i]);
}
return result;
}
};
动态规划 空间优化
- 写法1
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int>& array) {
int maxSum = array[0], result = maxnum;
for(int i=1; i<array.size(); i++)
{
if(maxSum + array[i] > array[i]) maxSum += array[i];
else maxSum = array[i];
result = max(result, maxSum);
}
return result;
}
};
- 写法2
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int>& array) {
int maxSum = array[0], result = maxSum;
//写法2
for(int i=1; i<array.size(); i++)
{
array[i] = max(0, array[i-1]) + array[i];
result = max(array[i], result);
}
return result;
}
};
补充内容
next_permutation
使用前必须先排序,返回全排列
#include <stdio.h>
#include <algorithm>
using namespace std;
int main(){
int n;
while(scanf("%d",&n)&&n){
int a[1000];
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
}
sort(a,a+n);
do{
for(int i=0;i<n;i++)
printf("%d ",a[i]);
printf("\n");
}while(next_permutation(a,a+n));
}
return 0;
}
堆排序
- 堆排序是利用堆性质进行的一种选择排序,堆是一棵顺序存储的完全二叉树,分为大顶堆和小顶堆。
- 每个节点的值都不大于其左右孩子节点的值的堆叫做小根堆(下左图)
- 每个节点的值都不小于其左右孩子节点的值的堆叫做大根堆(下右图)
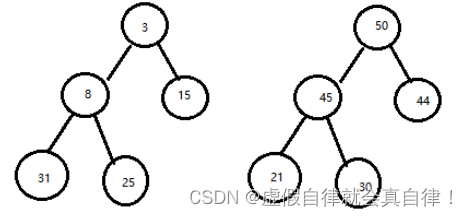
- 设当前元素array[i] 在数组array 下标是 i, 那么该元素:
- 左孩子结点下标是 2 * i + 1,对应结点值是 array[2*i+1]
- 右孩子结点下标是 2 * i + 2,对应结点值是 array[2*i+2]
- 父结点是:array[(i-1)/2];
- 小根堆:array[i] <= array[2*i+1] 且 array[i] <= array[2i+2]
- 大根堆:array[i] >= array[2*i+1] 且 array[i] >= array[2i+2]
-
大 / 小堆排序步骤如下:
(1)根据初始数组去构造初始堆,构建一个完全二叉树,保证所有的父结点都比它的孩子结点数值大 / 小。
(2)每次交换第一个和最后一个元素,输出最后一个元素,即最大值 / 最小值,然后把剩下元素重新调整为大根堆 / 小根堆。
(3)当输出完最后一个元素后,这个数组已经是按照从小到大 / 从小到大 的顺序排列了。 -
如何将整体数组构建成一个初始堆?
任选一颗完全二叉树,只需将根节点和左右孩子节点相互进行大小比较后交换数值,将较大值 / 较小值与根节点交换,如下
- 大顶堆
//对一颗完全二叉树的指定非叶子节点及其叶子结点进行堆的建立
void heapify(vector<int>& array, int len, int i)
{
//如果i>=len,证明数组中的元素都已经建立成大根堆了,递归终止
if(i >= len) return;
int left = 2 * i + 1; //左孩子节点的下标
int right = 2 * i + 2; //右孩子节点的下标
int max = i; //默认数值最大的节点为该非叶子节点的值
//判断左孩子节点是否在索引范围内及左孩子结点值是否大于根节点,大于的话就将较大值的下标记录在max中
if(left < len && array[left] > array[max]) max = left;
if(right < len && array[right] > array[max]) max = right;
if(max != i)
{
swap(array[i], array[max]);//如果最大值的下标改变,则需要交换两个下标所对应的值
heapify(array, len, max); //对剩下的不是完全二叉树的元素继续进行堆的建立
}
}
- 小顶堆
//对一颗完全二叉树的指定非叶子节点及其叶子结点进行堆的建立
void heapify(vector<int>& array, int len, int i)
{
//如果i>=len,证明数组中的元素都已经建立成小根堆了,递归终止
if(i >= len) return;
int left = 2 * i + 1; //左孩子节点的下标
int right = 2 * i + 2; //右孩子节点的下标
int min = i; //默认数值最小的节点为该非叶子节点的值
//判断左孩子节点是否在索引范围内及左孩子结点值是否小于根节点,小于的话就将较大值的下标记录在min中
if(left < len && array[left] < array[min]) min = left;
if(right < len && array[right] < array[min]) min = right;
if(min != i)
{
swap(array[i], array[min]);//如果最小值的下标改变,则需要交换两个下标所对应的值
heapify(array, len, min); //对剩下的不是完全二叉树的元素继续进行堆的建立
}
}
- 对于一棵完全二叉树应该从哪个结点开始建立堆?
一般从最后一个非叶子结点开始建立堆,假设二叉树结点总数为 n,那么最后一个非叶子结点是第 n/2 个,即根节点int root = (last_node - 1) / 2;
void buildHeap(vector<int>& array, int len)
{
int lastNodeindex = array.size()-1;//结点总数
//最后一个非叶子就是第lastNodeindex /2 个
//从一棵树的最后一个非叶子节点开始建立堆
int root = (lastNodeindex-1) >> 1;//等价于(lastNodeindex - 1)/2
for(int i=root; i>=0; --i)
heapify(array, len, i);
}
- 堆排序
堆排序就是重复将第一个最大的元素与最后一个叶子结点进行交换,然后输出交换后的最后一个叶子结点,再将剩下的元素进行调整,即调整成大根堆 / 小根堆,如此循环,直到所有元素都排好序。
void myTopk(vector<int>& array, int len, int k)
{
buildHeap(array, len);
for(int i=len-1; i>=0 && k; --i)
{
swap(array[i], array[0]);
result.push_back(array[i]);
--k;
heapify(array, i, 0);
}
}