目录
- 01.BST的介绍
- 02.BST 要实现的对外方法
- 03.摘要
- 04.查找节点
- 4.1四个引用,都有妙用
- 4.2递归版
- 4.3非递归版
- 05.插入节点
- 5.1利用search的返回值
- 5.2更新高度的注意事项
- 5.3插入算法的完整代码
- 06.删除节点
- 6.1框架
- 6.2单分支,直接替代
- 6.3双分支,化繁为简
- 6.4代码
- 07.code BST
- 树的后续
预告:本文是后续实现各种各样平衡二叉搜索树的铺垫。
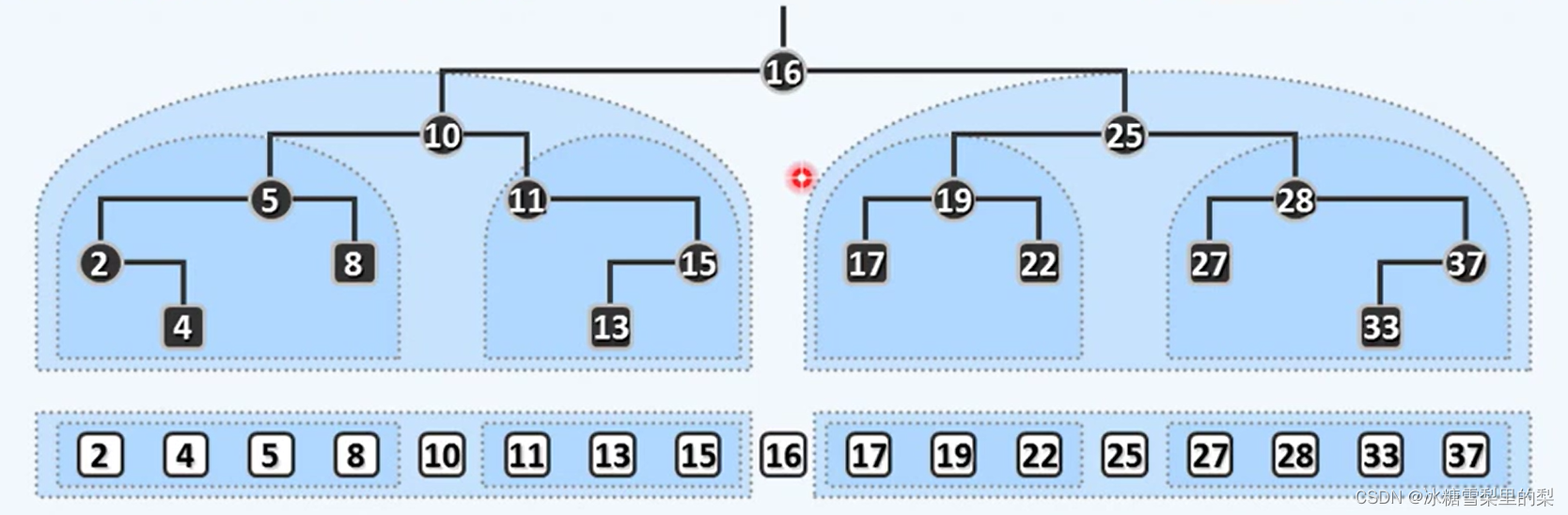
01.BST的介绍
- BST 寻关键码访问 (call by key)
相比于——
Vector call by rank
List call by position
Hash table call by value - 有序性
- 单调性
扩:从不可重复到可重复的扩充(下图)


02.BST 要实现的对外方法
| 方法 | 功能 | 参数 | 返回值 |
|---|---|---|---|
| search | 查找 | T const & val | BinNode * & 待插入位置/目标节点指针的引用 |
| insert | 插入 | BinNode * 新节点指针 | |
| remove | 移除 | bool 树上是否存在值为val的节点 |
03.摘要
- 虚函数,方便派生类进行重写。
- 全局静态模板函数,适用于AVL,Splay,RedBlack等各种BST
- 这里的remove一看就是对外的,因为参数终于不是指针了,而是值。需要我们先找位置。
- return searchIn(BinTree::root, hot = NULL, val); 注意 =NULL
04.查找节点
4.1四个引用,都有妙用
看到searchIn的声明,居然全都是引用类型。
static BinNode<T> * & searchIn(BinNode<T> * & rt, BinNode<T> * & hot_node, T const & val)
列举这四个引用各自的功能——
返回值引用:插入节点时,这个引用相当于插入位置,后续我们将新节点的指针赋给到这个返回值,父节点的左右孩子之一就会连上新节点。
BinNode<T> * & rt:如果这个不是引用,返回值返回的就是一个仅在函数内部的局部变量(即形参),后续改写这个引用值时,会发生错误。
BinNode<T> * & hot_node:在递归中随深度不断更新这个记忆热点,也是为了方便插入算法,等到最后退出时hot存的是插入位置的父节点。
T const & val:传递引用变量可以提速,为了不误改,前面加上const做约束。
4.2递归版
virtual BinNode<T> * & search(T const & val)
{
return searchIn(BinTree<T>::root, hot = NULL, val); //注意,这个=NULL,如果不写,插入根节点并向上更新高度时就会报错
}
static BinNode<T> * & searchIn(BinNode<T> * & rt, BinNode<T> * & hot_node, T const & val)
{
if (!rt || rt->data == val) return rt; // 返回的是引用
hot_node = rt; //在递归中随深度不断更新
if (val < rt->data) return searchIn(rt->left, hot_node, val);
else return searchIn(rt->right, hot_node, val);
}

4.3非递归版
尾递归转迭代,略。
05.插入节点
5.1利用search的返回值
有了查找节点算法中“记忆热点”hot的设计,经过search()的运行,就可以得到插入位置的父节点。或许应该记得BinTree里写过的几个函数:insertAsLeft(),insertAsRight(),我们只需要将val与hot->data做比较即可。在这里,我们换一种写法——不浪费search的返回值。你知道,查找一旦失败,返回值就是NULL的引用,利用它,就无需在insert()中判断究竟应该插入到hot的左边还是右边。
先找到插入位置,X的类型必须是引用,后续我们将新节点的指针赋给到X,hot的左右孩子之一就会连上新节点。
BinNode<T> * & X = search(val);
下面这一句话将 “父->子” “子->父” 相互关系都连接好了。
X = new BinNode(val, hot);

5.2更新高度的注意事项
更新高度由于之前做的优化,检测到某处更新后与更新前高度一致则不会再上行更新,所以高度更新要给父节点更新,即updateHighAbove(hot),如果给了X更新,那就不会继续下去。
5.3插入算法的完整代码
virtual BinNode<T> * insert(T const & val)
{
BinNode<T> * & X = search(val); //为了找到插入位置
if (!X)
{
X = new BinNode(val, hot); //这一句话将两个关系连接
// 不要忘记
BinTree<T>::size++;
updateHighAbove(hot);
}
return X;
}
insert()的返回值是X,但返回类型是BinNode<T> *,并不是引用,这在语法中是允许的。所返回的东西仅仅在数值上与X相同,但与X完全脱离了关系。
06.删除节点
6.1框架
virtual bool remove(T const & val)
{
BinNode<T> * & X = search(val);
if (!X) //树里没有val
{
return false;
}
else
{
removeAt(X, hot);
BinTree<T>::size--;
updateHighAbove(hot);
return true;
}
}
6.2单分支,直接替代

6.3双分支,化繁为简
还是想,哪一个节点替代被删节点的位置。那一定是直接后继。求中序遍历下的直接后继。
// struct BinNode中,功能:求中序遍历下的直接后继
BinNode<T> * succ()
{
BinNode<T> * succ_node;
if (right)
{
succ_node = right;
while (succ_node->left)
succ_node = succ_node->left;
}
else
{
succ_node = this;
while (succ_node != succ_node->parent->left)
succ_node = succ_node->parent;
succ_node = succ_node->parent;
}
return succ_node;
}

6.4代码
static BinNode<T> * removeAt(BinNode<T> * X, BinNode<T> * & hot_node)
{
// hot_node指向要被删除的父亲
BinNode<T> * del_node; // 实际要被删除的节点
BinNode<T> * succ_node; // 实际要被删除的节点的接替者
if (!X->left)
{
del_node = X;
succ_node = X->right;
}
else if (!X->right)
{
del_node = X;
succ_node = X->left;
}
else // 双分支情况
{
// 找到中序的直接后继
del_node = X->succ();
succ_node = del_node->right;
swap(del_node->data, X->data);
BinNode<T>::fromParentTo(del_node) = succ_node;
}
hot_node = del_node->parent;
if (succ_node) succ_node->parent = hot_node;
delete del_node;
return succ_node;
}
07.code BST
# pragma once
# include "BinTree.h"
template <typename T>
void swap(T & a, T & b)
{
T t;
t = a;
a = b;
b = t;
}
template <typename T>
class BST : public BinTree<T> {
public:
//***********************************************************查找*********************************************************
virtual BinNode<T> * & search(T const & val)
{
return searchIn(BinTree<T>::root, hot = NULL, val);
}
static BinNode<T> * & searchIn(BinNode<T> * & rt, BinNode<T> * & hot_node, T const & val)
{
if (!rt || rt->data == val) return rt; // 返回的是引用
hot_node = rt; //在递归中随深度不断更新
if (val < rt->data) return searchIn(rt->left, hot_node, val);
else return searchIn(rt->right, hot_node, val);
}
//***********************************************************插入*********************************************************
virtual BinNode<T> * insert(T const & val)
{
BinNode<T> * & X = search(val); //为了找到插入位置
if (!X)
{
X = new BinNode<T>(val, hot); //这一句话将两个关系连接
// 不要忘记
BinTree<T>::size++;
BinTree<T>::updateHighAbove(hot);
}
return X;
}
//***********************************************************删除*********************************************************
virtual bool remove(T const & val)
{
BinNode<T> * & X = search(val);
if (!X) //树里没有val
{
return false;
}
else
{
removeAt(X, hot);
BinTree<T>::size--;
BinTree<T>::updateHighAbove(hot);
return true;
}
}
static BinNode<T> * removeAt(BinNode<T> * X, BinNode<T> * & hot_node)
{
// hot_node指向要被删除的父亲
BinNode<T> * del_node; // 实际要被删除的节点
BinNode<T> * succ_node; // 实际要被删除的节点的接替者
if (!X->left)
{
del_node = X;
succ_node = X->right;
}
else if (!X->right)
{
del_node = X;
succ_node = X->left;
}
else // 双分支情况
{
// 找到中序的直接后继
del_node = X->succ();
succ_node = del_node->right;
swap(del_node->data, X->data);
BinNode<T>::fromParentTo(del_node) = succ_node;
}
hot_node = del_node->parent;
if (succ_node) succ_node->parent = hot_node;
delete del_node;
return succ_node;
}
//******************************************************统一重平衡算法****************************************************
// 在AVL中有极大用处
BinNode<T> * connect34(BinNode<T> *, BinNode<T> *, BinNode<T> *, BinNode<T> *, BinNode<T> *, BinNode<T> *, BinNode<T> *);
BinNode<T> * rotateAt(BinNode<T> * x);
protected:
BinNode<T> * hot; // 命中节点的父亲
};
谢谢观看~
树的后续
C++数据结构之平衡二叉搜索树(一)——AVL的实现(zig-zag/左右双旋/3+4重构)