本篇文章为 LeetCode 模拟模块的刷题笔记,仅供参考。
目录
- 一. 字符串
- Leetcode43.字符串相乘
- Leetcode592.分数加减运算
- Leetcode68.文本左右对齐
- 二. 矩阵
- Leetcode54.螺旋矩阵
- Leetcode885.螺旋矩阵 III
- Leetcode498.对角线遍历
- Leetcode874.模拟行走机器人
- 三. 数组
- Leetcode495.提莫攻击
- Leetcode735.行星碰撞
- 四. 栈
- Leetcode946.验证栈序列
- Leetcode1441.用栈操作构建数组
一. 字符串
字符串模拟题中最常见的就是加减乘除等基本运算,一种是使用字符串模拟大整数的基本运算,另一种是切片字符串表达式计算结果。字符串的模拟题还有文本对齐等情况;
Leetcode43.字符串相乘
Leetcode43.字符串相乘
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
注意:不能使用任何内置的 BigInteger 库或直接将输入转换为整数。
示例 1:
输入: num1 = “2”, num2 = “3”
输出: “6”
示例 2:
输入: num1 = “123”, num2 = “456”
输出: “56088”
提示:
1 <= num1.length, num2.length <= 200
num1 和 num2 只能由数字组成。
num1 和 num2 都不包含任何前导零,除了数字0本身。
模拟乘法的移位累加过程即可,加减乘除只限对一位使用,否则会溢出:
class Solution {
public:
string strplusstr(string s1,string s2){
if(s1.size()<s2.size()){
string tmp=s2;
s2=s1;
s1=tmp;
}
vector<char> v;
int n1=s1.size(); // n1>=n2
int n2=s2.size();
int s=0,c=0; // 和&进位
for(int i=0;i<n1;i++){
if(i>=n2){
s=c+(s1[n1-1-i]-'0');
c=s/10;
s=s%10;
v.push_back('0'+s);
}else{
s=c+(s1[n1-1-i]-'0')+(s2[n2-1-i]-'0');
c=s/10;
s=s%10;
v.push_back('0'+s);
}
}
if(c>0) v.push_back('0'+c); // 最高位进位
while(v.back()==0 && v.size()>1) v.pop_back(); // 去除前导零
string ans="";
for(int i=v.size()-1;i>=0;i--){
ans.push_back(v[i]);
}
return ans;
}
string multiply(string num1, string num2) {
string ans="0";
for(int i=num2.size()-1;i>=0;i--){
string tmp="0";
for(int j=num1.size()-1;j>=0;j--){
string s0(num1.size()-j-1,'0');
tmp=strplusstr(tmp,to_string((num1[j]-'0')*(num2[i]-'0'))+s0);
}
string s0(num2.size()-i-1,'0');
ans=strplusstr(ans,tmp+s0);
}
int i=0;
while(ans[i]=='0' && i<ans.size()-1) i++; // 去除前导零
return ans.substr(i);
}
};

Leetcode592.分数加减运算
Leetcode592.分数加减运算
给定一个表示分数加减运算的字符串 expression ,你需要返回一个字符串形式的计算结果。
这个结果应该是不可约分的分数,即最简分数。 如果最终结果是一个整数,例如 2,你需要将它转换成分数形式,其分母为 1。所以在上述例子中, 2 应该被转换为 2/1。
示例 1:
输入: expression = “-1/2+1/2”
输出: “0/1”
示例 2:
输入: expression = “-1/2+1/2+1/3”
输出: “1/3”
示例 3:
输入: expression = “1/3-1/2”
输出: “-1/6”
提示:
输入和输出字符串只包含 ‘0’ 到 ‘9’ 的数字,以及 ‘/’, ‘+’ 和 ‘-’。
输入和输出分数格式均为 ±分子/分母。如果输入的第一个分数或者输出的分数是正数,则 ‘+’ 会被省略掉。
输入只包含合法的最简分数,每个分数的分子与分母的范围是 [1,10]。 如果分母是1,意味着这个分数实际上是一个整数。
输入的分数个数范围是 [1,10]。
最终结果的分子与分母保证是 32 位整数范围内的有效整数。
在字符串中按➕和➖分割分数,然后将当前分数拆分后加到运算结果上即可。由于运算符号出现在被加 / 减数之前,因此维护变量 op 记录运算符号。分数相加时,通过 __gcd() 进行约分:
class Solution {
public:
void calfraction(int &n1,int &n2,string tmp,bool op){ // 分子、分母、当前分数、计算符号
int tmp1,tmp2;
for(int i=0;i<tmp.size();i++){
if(tmp[i]=='/'){
tmp1=stoi(tmp.substr(0,i));
tmp2=stoi(tmp.substr(i+1));
break;
}
}
if(op) n1=n1*tmp2-n2*tmp1;
else n1=n1*tmp2+n2*tmp1;
n2*=tmp2;
int gcd=abs(__gcd(n1,n2));
n1/=gcd;
n2/=gcd;
return;
}
string fractionAddition(string expression) {
int start=0,len=0;
int n1=0,n2=1;
bool op=0; // +为0,-为1
for(int i=0;i<expression.size();i++){
if(expression[i]=='+'||expression[i]=='-'){
string tmp=expression.substr(start,len);
if(tmp.size()==0){
len++;
continue;
}
len=0;
start=i+1;
calfraction(n1,n2,tmp,op);
op=expression[i]=='+'?0:1;
}else{
len++;
}
}
string tmp=expression.substr(start);
calfraction(n1,n2,tmp,op);
return to_string(n1)+"/"+to_string(n2);
}
};

Leetcode68.文本左右对齐
Leetcode68.文本左右对齐
给定一个单词数组 words 和一个长度 maxWidth ,重新排版单词,使其成为每行恰好有 maxWidth 个字符,且左右两端对齐的文本。
你应该使用 “贪心算法” 来放置给定的单词;也就是说,尽可能多地往每行中放置单词。必要时可用空格 ’ ’ 填充,使得每行恰好有 maxWidth 个字符。
要求尽可能均匀分配单词间的空格数量。如果某一行单词间的空格不能均匀分配,则左侧放置的空格数要多于右侧的空格数。
文本的最后一行应为左对齐,且单词之间不插入额外的空格。
注意:
单词是指由非空格字符组成的字符序列。
每个单词的长度大于 0,小于等于 maxWidth。
输入单词数组 words 至少包含一个单词。
示例 1:
输入: words = [“This”, “is”, “an”, “example”, “of”, “text”, “justification.”], maxWidth = 16
输出:
[
“This is an”,
“example of text”,
"justification. "
]
示例 2:
输入:words = [“What”,“must”,“be”,“acknowledgment”,“shall”,“be”], maxWidth = 16
输出:
[
“What must be”,
"acknowledgment ",
"shall be "
]
解释: 注意最后一行的格式应为 "shall be " 而不是 “shall be”,
因为最后一行应为左对齐,而不是左右两端对齐。
第二行同样为左对齐,这是因为这行只包含一个单词。
示例 3:
输入:words = [“Science”,“is”,“what”,“we”,“understand”,“well”,“enough”,“to”,“explain”,“to”,“a”,“computer.”,“Art”,“is”,“everything”,“else”,“we”,“do”],maxWidth = 20
输出:
[
“Science is what we”,
“understand well”,
“enough to explain to”,
“a computer. Art is”,
“everything else we”,
"do "
]
提示:
1 <= words.length <= 300
1 <= words[i].length <= 20
words[i] 由小写英文字母和符号组成
1 <= maxWidth <= 100
words[i].length <= maxWidth
题干表述不清,需要注意,每个单词间至少需要保持一个空格。先根据单词长度计算每行能够放置的单词数量和相应的单词长度,然后对每行的字符串进行拼接。最后一行左对齐单独处理,前 n-1 行均分空格。为了处理多余空格,设计 getspacenum 函数,通过比较当前单词位置与多余空格数量,即可得到当前位置需要拼接的空格数量:
class Solution {
public:
string fillempty(int n){
string s="";
for(int i=0;i<n;i++){
s+=" ";
}
return s;
}
int getspacenum(int curlen, int maxlen,int curnum,int cnt){
assert(curnum>1);
int d=(maxlen-curlen)/(curnum-1);
int r=(maxlen-curlen)%(curnum-1);
if(cnt>=r) return d;
else return d+1; // 前r个位置多一个空格
}
vector<string> fullJustify(vector<string>& words, int maxWidth) {
vector<int> vnum; // 每行单词数量
vector<int> vlen; // 每行单词总长度
int num=1;
int len=words[0].size();
for(int i=1;i<words.size();i++){
if((len+1+words[i].size())<=maxWidth){
len+=(1+words[i].size()); // +1因为单词间至少一个空格
}else{
vnum.push_back(num);
vlen.push_back(len);
len=words[i].size();
num=0;
}
num++;
}
if(num!=0){ // 最后一行还没存入数组
vnum.push_back(num);
vlen.push_back(len);
}
int n=vnum.size();
// for(int i=0;i<n;i++){
// cout<<vnum[i]<<" "<<vlen[i]<<endl;
// }
vector<string> ans(n);
int cnt=0;
for(int i=0;i<n;i++){
if(i==n-1){ // 最后一行左对齐
string s=words[cnt++];
for(int j=1;j<vnum[i];j++){
s+=" "+words[cnt++];
}
s+=fillempty(maxWidth-vlen[i]);
ans[i]=s;
}
else{ // 前n-1行均分空格
if(vnum[i]==1){ // 只有一个单词的行需要单独处理空格
ans[i]=words[cnt++]+fillempty(maxWidth-vlen[i]);
}
else{
string s=words[cnt++];
for(int j=1;j<vnum[i];j++){
s+=fillempty(getspacenum(vlen[i],maxWidth,vnum[i],j-1)+1)+words[cnt++];
}
ans[i]=s;
}
}
}
return ans;
}
};

二. 矩阵
Leetcode54.螺旋矩阵
Leetcode54.螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100
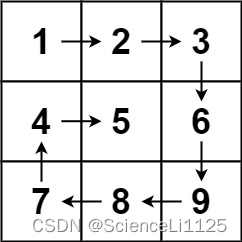
画出螺旋路径图如下:

四个顶点是改变搜索方向的转折点,因此只需要 判断是否到达四个转折点 即可:
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
int i=0,j=0; // 当前位置
int cnt=0; // 已搜索数量
int direct=0; // 搜索方向(0:左右;1:上下;2:右左;3:下上)
int m=matrix.size();
int n=matrix[0].size();
int curm=m; // 当前长/宽
int curn=n;
vector<int> ans(m*n);
while(cnt<m*n){
ans[cnt]=matrix[i][j];
if(direct==0){ // 左->右
if(i==(m-curm)/2 && j==(n+curn)/2-1){ //右上
direct=1; // 换方向
i++;
}else{
j++;
}
}else if(direct==1){ // 上->下
if(i==(m+curm)/2-1 && j==(n+curn)/2-1){ //右下
direct=2; // 换方向
j--;
}else{
i++;
}
}else if(direct==2){ // 右->左
if(i==(m+curm)/2-1 && j==(n-curn)/2){ //左下
direct=3; // 换方向
i--;
}else{
j--;
}
}else if(direct==3){ // 下->上
if(i==(m-curm)/2+1 && j==(n-curn)/2){ //左上
direct=0; // 换方向
j++;
curm-=2; // 调整当前长/宽
curn-=2;
}else{
i--;
}
}
cnt++;
}
return ans;
}
};

上述写法可以简化,即使用 dx, dy 作为 x 和 y 的方向增量,可以省去 direct 标记。
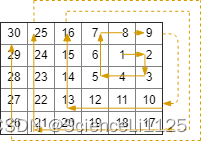
Leetcode885.螺旋矩阵 III
Leetcode885.螺旋矩阵 III
在 rows x cols 的网格上,你从单元格 (rStart, cStart) 面朝东面开始。网格的西北角位于第一行第一列,网格的东南角位于最后一行最后一列。
你需要以顺时针按螺旋状行走,访问此网格中的每个位置。每当移动到网格的边界之外时,需要继续在网格之外行走(但稍后可能会返回到网格边界)。
最终,我们到过网格的所有 rows x cols 个空间。
按照访问顺序返回表示网格位置的坐标列表。
示例 1:
输入:rows = 1, cols = 4, rStart = 0, cStart = 0
输出:[[0,0],[0,1],[0,2],[0,3]]
示例 2:
输入:rows = 5, cols = 6, rStart = 1, cStart = 4
输出:[[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]
提示:
1 <= rows, cols <= 100
0 <= rStart < rows
0 <= cStart < cols
螺旋路径其实有两种考虑方向,一种是考虑 改变方向的转折点,另一种是考虑 螺旋半径。Leetcode54.螺旋矩阵 中的做法是考虑转折点,本题给出考虑螺旋半径的做法。
不要被题目的描述唬住了,本质就是一个从内向外的螺旋遍历。遍历时判断坐标是否在 rows × cols 的范围内,若在范围内则压入数组 ans 即可。从内向外螺旋遍历时,维护一个不断增大的螺旋半径 R,当前方向走到 R 步时需要调整方向,每调整两次方向 R 就增大 1。while 循环遍历即可,直到数组 ans 中有 rows × cols 个元素:
class Solution {
public:
void direction(int &dx,int &dy){
if(dx==-1 && dy==0){ // 上
dx=0;
dy=1;
}else if(dx==0 && dy==1){ // 右
dx=1;
dy=0;
}else if(dx==1 && dy==0){ // 下
dx=0;
dy=-1;
}else if(dx==0 && dy==-1){ // 左
dx=-1;
dy=0;
}
}
vector<vector<int>> spiralMatrixIII(int rows, int cols, int rStart, int cStart) {
vector<vector<int>> ans;
int rCur=rStart,cCur=cStart;
int dx=0,dy=1;
int R=1; // 螺旋半径
int curR=0; // 当前走过的螺旋半径
bool flag=0;
while(ans.size()<rows*cols){
if(rCur>=0 && rCur<rows && cCur>=0 && cCur<cols){
ans.push_back({rCur,cCur});
}
if(curR==R){
direction(dx,dy);
R+=flag;
curR=0;
flag=flag?0:1;
}
rCur+=dx;
cCur+=dy;
curR++;
}
return ans;
}
};

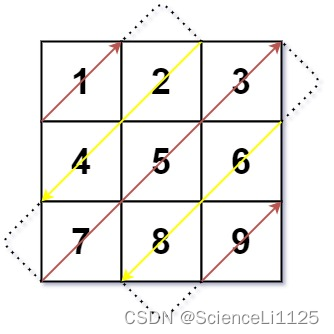
Leetcode498.对角线遍历
Leetcode498.对角线遍历
给你一个大小为 m x n 的矩阵 mat ,请以对角线遍历的顺序,用一个数组返回这个矩阵中的所有元素。
示例 1:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,4,7,5,3,6,8,9]
示例 2:
输入:mat = [[1,2],[3,4]]
输出:[1,2,3,4]
提示:
m == mat.length
n == mat[i].length
1 <= m, n <= 104
1 <= m * n <= 104
-105 <= mat[i][j] <= 105
副对角线的特点是每条线上 i + j 为定值,记为 k,因此可以以此遍历,总共需要遍历 m+n-1 条对角线。下面讨论对角线的起始位置:
- 若 k 为奇,则从上边或右边出发遍历;
- 若 k <= n-1,则从上边出发遍历;
- 若 k > n-1,则从右边出发遍历;
- 若 k 为偶,则从左边或下边出发遍历;
- 若 k <= m-1,则从左边出发遍历;
- 若 k > m-1,则从下边出发遍历;
class Solution {
public:
vector<int> findDiagonalOrder(vector<vector<int>>& mat) {
int m=mat.size();
int n=mat[0].size();
vector<int> ans;
for(int k=0;k<m+n-1;k++){
int x,y,dx,dy;
if(k%2==0){
if(k<=m-1){ // 左
x=k;
y=0;
}else{ // 下
x=m-1;
y=k-m+1;
}
dx=-1;
dy=1;
}else{
if(k<=n-1){ // 上
x=0;
y=k;
}else{ // 右
x=k-n+1;
y=n-1;
}
dx=1;
dy=-1;
}
while(x>=0&&x<m&&y>=0&&y<n){
ans.push_back(mat[x][y]);
x+=dx;
y+=dy;
}
}
return ans;
}
};

Leetcode874.模拟行走机器人
Leetcode874.模拟行走机器人
机器人在一个无限大小的 XY 网格平面上行走,从点 (0, 0) 处开始出发,面向北方。该机器人可以接收以下三种类型的命令 commands :
-2 :向左转 90 度
-1 :向右转 90 度
1 <= x <= 9 :向前移动 x 个单位长度
在网格上有一些格子被视为障碍物 obstacles 。第 i 个障碍物位于网格点 obstacles[i] = (xi, yi) 。
机器人无法走到障碍物上,它将会停留在障碍物的前一个网格方块上,但仍然可以继续尝试进行该路线的其余部分。
返回从原点到机器人所有经过的路径点(坐标为整数)的最大欧式距离的平方。(即,如果距离为 5 ,则返回 25 )
注意:
北表示 +Y 方向。
东表示 +X 方向。
南表示 -Y 方向。
西表示 -X 方向。
示例 1:
输入:commands = [4,-1,3], obstacles = []
输出:25
解释:
机器人开始位于 (0, 0):
- 向北移动 4 个单位,到达 (0, 4)
- 右转
- 向东移动 3 个单位,到达 (3, 4)
距离原点最远的是 (3, 4) ,距离为 32 + 42 = 25
示例 2:
输入:commands = [4,-1,4,-2,4], obstacles = [[2,4]]
输出:65
解释:机器人开始位于 (0, 0):
- 向北移动 4 个单位,到达 (0, 4)
- 右转
- 向东移动 1 个单位,然后被位于 (2, 4) 的障碍物阻挡,机器人停在 (1, 4)
- 左转
- 向北走 4 个单位,到达 (1, 8)
距离原点最远的是 (1, 8) ,距离为 12 + 82 = 65
提示:
1 <= commands.length <= 104
commands[i] is one of the values in the list [-2,-1,1,2,3,4,5,6,7,8,9].
0 <= obstacles.length <= 104
-3 * 104 <= xi, yi <= 3 * 104
答案保证小于 231
需要注意的是,本题的 x 和 y 使用的不是 矩阵的下标,而是 坐标系的坐标,x 加减表示左右移动,y 加减表示上下移动。
有几个测试样例比较逆天,obstacles 中包含了出发点 [0, 0],因此函数 isblocked 中判断 obstacles[i][0] 或 obstacles[i][1] 范围时 x 或 y 的那一边不能挂等号。
class Solution {
public:
void direction(int command,int &dx,int &dy){
if(command==-1){ // 右转
if(dx==0 && dy==1){ // 北
dx=1;
dy=0;
}else if(dx==1 && dy==0){ // 东
dx=0;
dy=-1;
}else if(dx==0 && dy==-1){ // 南
dx=-1;
dy=0;
}else if(dx==-1 && dy==0){ // 西
dx=0;
dy=1;
}
}else if(command==-2){ // 左转
if(dx==0 && dy==1){ // 北
dx=-1;
dy=0;
}else if(dx==-1 && dy==0){ // 西
dx=0;
dy=-1;
}else if(dx==0 && dy==-1){ // 南
dx=1;
dy=0;
}else if(dx==1 && dy==0){ // 东
dx=0;
dy=1;
}
}
}
void isblocked(int &x,int &y,int tx,int ty,vector<vector<int>>& obstacles){
if(x==tx && y<ty){ // 南->北
int tmp=ty;
for(int i=0;i<obstacles.size();i++){
if(obstacles[i][0]==x && obstacles[i][1]>y && obstacles[i][1]<=ty){
tmp=min(tmp,obstacles[i][1]-1);
}
}
y=tmp;
}else if(x==tx && y>ty){ // 北->南
int tmp=ty;
for(int i=0;i<obstacles.size();i++){
if(obstacles[i][0]==x && obstacles[i][1]>=ty && obstacles[i][1]<y){
tmp=max(tmp,obstacles[i][1]+1);
}
}
y=tmp;
}else if(y==ty && x<tx){ // 西->东
int tmp=tx;
for(int i=0;i<obstacles.size();i++){
if(obstacles[i][1]==y && obstacles[i][0]>x && obstacles[i][0]<=tx){
tmp=min(tmp,obstacles[i][0]-1);
}
}
x=tmp;
}else if(y==ty && x>tx){ // 东->西
int tmp=tx;
for(int i=0;i<obstacles.size();i++){
if(obstacles[i][1]==y && obstacles[i][0]>=tx && obstacles[i][0]<x){
tmp=max(tmp,obstacles[i][0]+1);
}
}
x=tmp;
}
}
int robotSim(vector<int>& commands, vector<vector<int>>& obstacles) {
int dx=0,dy=1; // 方向
int x=0,y=0; // 位置
int ans=0;
for(int i=0;i<commands.size();i++){
if(commands[i]==-1 || commands[i]==-2){
direction(commands[i],dx,dy);
}else{
int tx=x+commands[i]*dx;
int ty=y+commands[i]*dy;
isblocked(x,y,tx,ty,obstacles);
ans=max(ans,x*x+y*y);
}
}
return ans;
}
};
上述代码耗时较长,第一次提交时还超出了时间限制:

三. 数组
数组模拟常用的切入点是观察相邻数据的关系。
Leetcode495.提莫攻击
Leetcode495.提莫攻击
在《英雄联盟》的世界中,有一个叫 “提莫” 的英雄。他的攻击可以让敌方英雄艾希(编者注:寒冰射手)进入中毒状态。
当提莫攻击艾希,艾希的中毒状态正好持续 duration 秒。
正式地讲,提莫在 t 发起攻击意味着艾希在时间区间 [t, t + duration - 1](含 t 和 t + duration - 1)处于中毒状态。如果提莫在中毒影响结束 前 再次攻击,中毒状态计时器将会 重置 ,在新的攻击之后,中毒影响将会在 duration 秒后结束。
给你一个 非递减 的整数数组 timeSeries ,其中 timeSeries[i] 表示提莫在 timeSeries[i] 秒时对艾希发起攻击,以及一个表示中毒持续时间的整数 duration 。
返回艾希处于中毒状态的 总 秒数。
示例 1:
输入:timeSeries = [1,4], duration = 2
输出:4
解释:提莫攻击对艾希的影响如下:
- 第 1 秒,提莫攻击艾希并使其立即中毒。中毒状态会维持 2 秒,即第 1 秒和第 2 秒。
- 第 4 秒,提莫再次攻击艾希,艾希中毒状态又持续 2 秒,即第 4 秒和第 5 秒。
艾希在第 1、2、4、5 秒处于中毒状态,所以总中毒秒数是 4 。
示例 2:
输入:timeSeries = [1,2], duration = 2
输出:3
解释:提莫攻击对艾希的影响如下:
- 第 1 秒,提莫攻击艾希并使其立即中毒。中毒状态会维持 2 秒,即第 1 秒和第 2 秒。
- 第 2 秒,提莫再次攻击艾希,并重置中毒计时器,艾希中毒状态需要持续 2 秒,即第 2 秒和第 3 秒。
艾希在第 1、2、3 秒处于中毒状态,所以总中毒秒数是 3 。
提示:
1 <= timeSeries.length <= 104
0 <= timeSeries[i], duration <= 107
timeSeries 按 非递减 顺序排列
虽然中毒状态是连续的,但中毒状态的开始和结束时刻是离散的,因此可以连续问题离散化。只需要看 timeSeries[i] 和 timeSeries[i+1] 之间的差值以及 duration 的持续时间大小即可:
class Solution {
public:
int findPoisonedDuration(vector<int>& timeSeries, int duration) {
int cnt=0;
for(int i=0;i<timeSeries.size()-1;i++){
cnt+=min(timeSeries[i+1]-timeSeries[i],duration);
}
return cnt+duration;
}
};

Leetcode735.行星碰撞
Leetcode735.行星碰撞
给定一个整数数组 asteroids,表示在同一行的行星。
对于数组中的每一个元素,其绝对值表示行星的大小,正负表示行星的移动方向(正表示向右移动,负表示向左移动)。每一颗行星以相同的速度移动。
找出碰撞后剩下的所有行星。碰撞规则:两个行星相互碰撞,较小的行星会爆炸。如果两颗行星大小相同,则两颗行星都会爆炸。两颗移动方向相同的行星,永远不会发生碰撞。
示例 1:
输入:asteroids = [5,10,-5]
输出:[5,10]
解释:10 和 -5 碰撞后只剩下 10 。 5 和 10 永远不会发生碰撞。
示例 2:
输入:asteroids = [8,-8]
输出:[]
解释:8 和 -8 碰撞后,两者都发生爆炸。
示例 3:
输入:asteroids = [10,2,-5]
输出:[10]
解释:2 和 -5 发生碰撞后剩下 -5 。10 和 -5 发生碰撞后剩下 10 。
提示:
2 <= asteroids.length <= 104
-1000 <= asteroids[i] <= 1000
asteroids[i] != 0
若相邻两个行星左边的向右,右边的向左则会发生碰撞。从左向右遍历数组,若出现碰撞,则从该元素开始向前更新碰撞后的行星状态:
class Solution {
public:
void bomb(int planet,vector<int>& ans){
// ans.back()<0
if(ans.size()==0 || ans.back()<0){
ans.push_back(planet);
return;
}
// ans.back()>0
else if((ans.back()+planet)==0){
ans.pop_back();
return;
}
else if((ans.back()+planet)>0){
return;
}
else{
ans.pop_back();
bomb(planet,ans);
return;
}
}
vector<int> asteroidCollision(vector<int>& asteroids) {
vector<int> ans(1,asteroids[0]);
for(int i=1;i<asteroids.size();i++){
if(ans.size()>0 && ans.back()>0 && asteroids[i]<0){
bomb(asteroids[i],ans);
}else{
ans.push_back(asteroids[i]);
}
}
return ans;
}
};

四. 栈
栈相关的模拟题一般都需要用指针进行记录。
Leetcode946.验证栈序列
Leetcode946.验证栈序列
给定 pushed 和 popped 两个序列,每个序列中的 值都不重复,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 true;否则,返回 false 。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。
提示:
1 <= pushed.length <= 1000
0 <= pushed[i] <= 1000
pushed 的所有元素 互不相同
popped.length == pushed.length
popped 是 pushed 的一个排列
将 pushed 数组中的元素依次压栈,如果遇到 popped 数组的当前元素与栈顶元素相同则弹出,然后 popped 数组后移一位,如果与栈顶元素仍相同则继续弹出直至不同。重复执行上述操作直到 pushed 数组为空。当 pushed 数组为空时,遍历 popped 数组中的剩余元素,若与栈中元素出栈顺序一致则返回 true,否则为 false:
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
stack<int> stk;
int ptr1=0,ptr2=0;
int n=pushed.size();
while(ptr1<n){
stk.push(pushed[ptr1]);
while(!stk.empty() && stk.top()==popped[ptr2]){
stk.pop();
ptr2++;
}
ptr1++;
}
while(!stk.empty()){
if(popped[ptr2]==stk.top()){
stk.pop();
ptr2++;
}else{
return false;
}
}
return true;
}
};

Leetcode1441.用栈操作构建数组
Leetcode1441.用栈操作构建数组
给你一个数组 target 和一个整数 n。每次迭代,需要从 list = { 1 , 2 , 3 …, n } 中依次读取一个数字。
请使用下述操作来构建目标数组 target :
“Push”:从 list 中读取一个新元素, 并将其推入数组中。
“Pop”:删除数组中的最后一个元素。
如果目标数组构建完成,就停止读取更多元素。
题目数据保证目标数组严格递增,并且只包含 1 到 n 之间的数字。
请返回构建目标数组所用的操作序列。如果存在多个可行方案,返回任一即可。
示例 1:
输入:target = [1,3], n = 3
输出:[“Push”,“Push”,“Pop”,“Push”]
解释:
读取 1 并自动推入数组 -> [1]
读取 2 并自动推入数组,然后删除它 -> [1]
读取 3 并自动推入数组 -> [1,3]
示例 2:
输入:target = [1,2,3], n = 3
输出:[“Push”,“Push”,“Push”]
示例 3:
输入:target = [1,2], n = 4
输出:[“Push”,“Push”]
解释:只需要读取前 2 个数字就可以停止。
提示:
1 <= target.length <= 100
1 <= n <= 100
1 <= target[i] <= n
target 严格递增
使用指针 ptr 记录当前操作过的数据,遍历 target 数组,如果 target[i] 大于 ptr,则说明该数据压入栈后又被弹出:
class Solution {
public:
vector<string> buildArray(vector<int>& target, int n) {
vector<string> ans;
int ptr=1;
for(int i=0;i<target.size();i++){
while(target[i]>ptr){
ans.push_back("Push");
ans.push_back("Pop");
ptr++;
}
ans.push_back("Push");
ptr++;
}
return ans;
}
};






![[CKA]考试之一个 Pod 封装多个容器](https://img-blog.csdnimg.cn/18d98d5ac52c4afc9b2f243bc3641b7a.png)