代码随想录刷题记录 day42 打家劫舍 1 2 3
参考:代码随想录
198. 打家劫舍

思想
1.dp[i]表示偷取[0,i]房间内获取的最高的金额
2.递推公式
-
偷取第i号房间时的价值
dp[i]=dp[i-2]+nums[i];
-
不偷取第i号房间时的价值
dp[i]=dp[i-1]
所以递推公式
dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i])
3.初始化
dp[0]=nums[0];
dp[1]=max(nums[0],nums[1]) ;
4.遍历顺序
从小到大
5.打印dp数组
nums=[1,2,3,1]
dp=[0,1,2,4,4]
代码
class Solution {
public int rob(int[] nums) {
//dp[i] 表示偷 [0,i]区间的房间能偷到的最高的金额
//考虑以下两种情况,
//1.偷第i间房 dp[i]=dp[i-2]+nums[i]
//2.不偷第i间房 dp[i]=dp[i-1] 考虑i-1房
if(nums.length==1) return nums[0];
int [] dp=new int[nums.length];
dp[0]=nums[0];
dp[1]=Math.max(nums[0],nums[1]);
if(nums.length==2) return dp[1];
for(int i=2;i<nums.length;i++){
dp[i]=Math.max(dp[i-2]+nums[i],dp[i-1]);
//System.out.println(dp[i]);
}
return dp[nums.length-1];
}
}
213. 打家劫舍 II

思想
考虑
偷首不偷尾
偷尾不偷首
首尾都不偷
偷首不偷尾和偷尾不偷首包括了首尾都不偷的情况
- 将偷首不偷尾所包含的数组区间传入上一题打家劫舍的逻辑得到res1
- 将偷尾不偷首所包含的数组区间传入上一题打家劫舍的逻辑得到res2
- 较大的就是所求的答案
代码
class Solution {
public int rob(int[] nums) {
//考虑首元素 考虑尾元素
if(nums.length==0) return 0;
if(nums.length==1) return nums[0];
int res1=robRange(nums,0,nums.length-2);//闭区间
int res2=robRange(nums,1,nums.length-1);
return Math.max(res1,res2);
}
public int robRange(int[] nums ,int start,int end){
if(end==start) return nums[start];//首元素=尾元素 直接返回
int [] dp=new int[nums.length];
dp[start]=nums[start];
dp[start+1]=Math.max(nums[start],nums[start+1]);
for(int i=start+2;i<=end;i++){
dp[i]=Math.max(dp[i-2]+nums[i],dp[i-1]);
}
return dp[end];
}
}
337. 打家劫舍 III
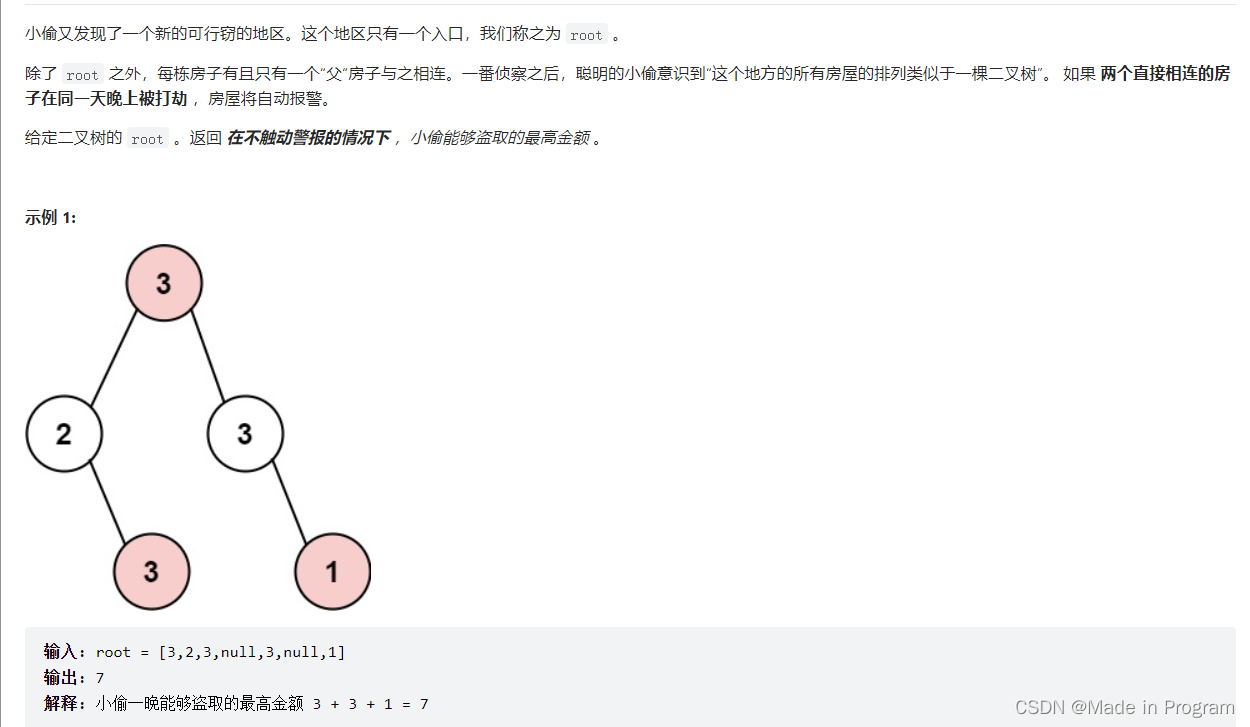
思想
-
dp[0]表示不偷取当前节点获得的价值,dp[1]表示偷取当前节点获得的价值
-
递推公式
-
不偷取当前节点
int val1=Math.max(left[0],left[1])+Math.max(right[0],right[1]);
-
偷取当前节点
int val2=node.val+left[0]+right[0];
-
-
终止条件和初始化
int[] dp=new int[2];
if(node.val==null) return dp;
-
遍历顺序
后序遍历
通过递归左节点,得到左节点偷与不偷的金钱。
通过递归右节点,得到右节点偷与不偷的金钱。
代码
class Solution {
public int rob(TreeNode root) {
int[] res=robRecursion(root);
return Math.max(res[0],res[1]);
}
public int[] robRecursion(TreeNode node){
int[] dp=new int[2];
if(node==null) return dp;
//dp[0] 表示不偷当前节点 dp[1] 表示偷当前节点
int[] left=robRecursion(node.left);
int[] right=robRecursion(node.right);
dp[0]=Math.max(left[0],left[1])+Math.max(right[0],right[1]);
dp[1]=node.val+left[0]+right[0];
return dp;
}
}