Java的方法怎么用？递归是什么？一篇文章带你醍醐灌顶

news2024/9/30 13:27:04

1.方法定义

2.实参形参

3.方法重载

4.递归

1.方法定义

// 方法定义
修饰符 返回值类型 方法名称([参数类型 形参 ...]){
方法体代码;
[return 返回值];
}
    public static 返回值 方法名(形式参数列表){
        
    }

实现一个函数，检测一个年份是否为闰年

    public class Method{
        // 方法定义
        public static boolean isLeapYear(int year){
            if((0 == year % 4 && 0 != year % 100) || 0 == year % 400){
                return true;
            }else{
                return false;
            }
        }
    }

注意：

1.返回的值数据类型要匹配，void可以不反悔

2.方法名字：小写

3.方法无参数，（）里面可以不写，有参数一定要指定参数类型

4.方法一定要写在类里面

5.方法不能嵌套定义

6.没有方法声明，因为Java是全局的

    public static int sum(int a, int b){//形参
        //System.out.println(a+b);
        return a+b;
    }
    public static void main(String[] args) {
        int x = 10;
        int y = 20;
        int ret = sum(x,y)//x和y是实参
        System.out.println(ret);
    }

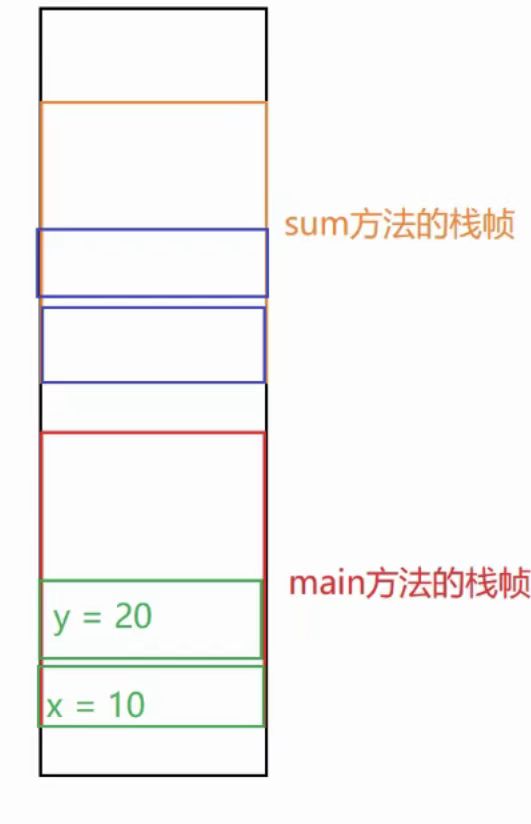
方法调用需要开辟内存，方法调用结束，这块内存就销毁

2.实参形参

Java 中方法的形参就相当于 sum 函数中的自变量 n ，用来接收 sum 函数在调用时传递的值的 。形参的名字可以随意取，对方法都没有任何影响，形参只是方法在定义时需要借助的一个变量，用来保存方法在调用时传递过来的值 。

    public static void main(String[] args) {
        int a = 10;
        int b = 20;
        System.out.println("交换前: a = " + a + " b = " + b);
        swap(a, b);
        System.out.println("交换后: a = " + a + " b = " + b);
    }
    public static void swap(int x, int y) {
        int tmp = x;
        x = y;
        y = tmp;
    }

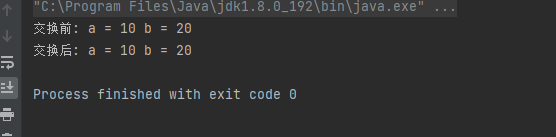
我们发现交换前和交换后a和b的值都没发生改变，这是因为实参 a 和 b 是 main 方法中的两个变量，其空间在 main 方法的栈 ( 一块特殊的内存空间 ) 中，而形参 x 和 y 是 swap 方法中的两个变量， x 和 y 的空间在 swap 方法运行时的栈中，因此：实参 a 和 b 与形参 x 和 y 是两个没有任何关联性的变量，

在 swap 方法调用时，只是将实参 a 和 b 中的值拷贝了一份传递给了形参 x 和 y ，因此对形参 x 和 y 操作不会对实参 a 和 b产生任何影响。

对于基础类型来说，形参相当于实参的拷贝，也就是传值调用

我们可以用数组来解决这个问题

    public static void main(String[] args) {
        int[] arr = {10, 20};
        swap(arr);
        System.out.println("arr[0] = " + arr[0] + " arr[1] = " + arr[1]);
    }
    public static void swap(int[] arr) {
        int tmp = arr[0];
        arr[0] = arr[1];
        arr[1] = tmp;
    }
}
// 运行结果
//arr[0] = 20 arr[1] = 10

3.方法重载

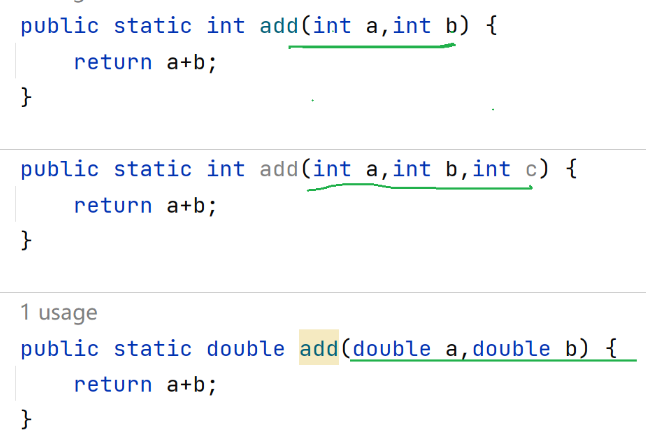
方法重载满足条件：

1.方法名必须相同

2.参数列表不同（个数，类型，顺序）

3.返回值不影响重载（不作为重载的判断条件）

那么编译器怎么分别这些方法的呢？

这就要提到方法签名了

方法签名即：经过编译器编译修改过之后方法最终的名字。具体方式： 方法全路径名 + 参数列表 + 返回值类型，构成 方法完整的名字

4.递归

执行过程

递归练习

按顺序打印一个数字的每一位

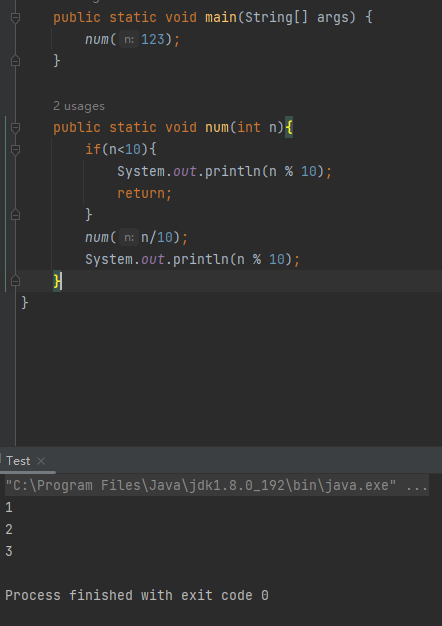
求斐波那契数列的第 N 项

    public static int fib(int n) {
        if (n == 1 || n == 2) {
            return 1;
        }
        return fib(n - 1) + fib(n - 2);
    }

当我们计算fib(4)时，我们需要计算fib(3)，计算fib(3)我们还要计算fib(2).....

如果数据量太大的话，会进行太多无用的重复计算

    public static int count = 0; 
    public static void main(String[] args) {
        System.out.println(fib(40));
        System.out.println(count);
    }
    public static int fib(int n) {
        if (n == 1 || n == 2) {
            return 1;
        }
        if (n == 3) {
            count++;
        }
        return fib(n - 1) + fib(n - 2);
    }
}
// 执行结果
//102334155 
//39088169 // fib(3) 重复执行了 3 千万次.

我们修改一下代码（用循环）

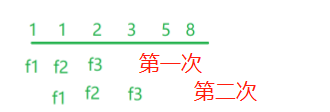
每次计算完f3就把三个数往后面推

    public static int fib2(int n){
        if(n == 1 || n == 2){
            return 1;
        }
        int f1 = 1;
        int f2 = 1;
        int f3 = 1;
        for (int i = 3; i <= n ; i++) {
            f3 = f1 + f2;
            f1 = f2;
            f2 = f3;
        }
        return f3;
    }