文章目录

链表基础
题型
- 一、单链表翻转、反转、旋转
- - 1.反转链表
  - 2.反转链表II——反转部分链表
  - 3.旋转链表
  - 4.K个一组翻转链表
  - 5.反转偶数长度组的节点
- 二、删除单链表中的结点
- - 1.删除链表的结点
  - 2.删除未排序链表中的重复节点
  - 3.删除已排序链表中的重复元素I——重复元素只剩下一个
  - 4.删除已排序链表中的重复元素II——重复元素全部删除
  - 5.删除链表的倒数第n个结点
  - 6.从链表中移除结点
  - 7.删除链表的中间结点
  - 8.从链表中删除总和值为零的连续节点
  - 9.删除链表中的结点
- 三、链表排序
- - 1.单链表排序
  - 2.合并k个升序单链表
  - 3.重排单链表
  - 4.排序的循环链表
  - 5.对单链表进行插入排序
- 四、回文链表
- - 1.判断回文链表
- 五、环形链表
- - 1.判断环形链表：判断链表中是否存在环，如图：链表尾部结点连接到了链表中间结点。
  - 2.环形链表II：返回链表开始入环的第一个节点。如果链表无环，则返回 null。
- 六、获取链表结点
- - 1.返回倒数第k个节点
  - 5.交换链表节点
- 七、链表相交
- 八、链表合并
- 九、链表的计算
- - 1.两数相加II
  - 3.链表最大孪生和
  - 4.二进制链表转整数
- 十、分割链表
- - 1.分割链表
  - 2.分隔链表
- 链表与二叉树
- - 1.BiNode
  - 2.特定深度结点链表
  - 3.二叉树中的链表
  - 4.填充每个结点的下一个右侧节点指针
  - 5.二叉树展开为链表
  - 6.有序链表转化平衡二叉搜索树
- 通过链表解题
- - 1.使数组按非递减顺序排列——链表+单调栈
- 链表的复制
- - 1.复杂链表的复制
- 双向链表
- - 1.扁平化多级双向链表
  - 2.二叉搜索树与双向循环链表
- 链表设计题
- - 1.设计哈希集合
  - 2.LRU缓存
  - 3.LFU缓存
  - 4.设计浏览器缓存
  - 5.设计循环队列
  - 6.设计循环双端队列
  - 7.设计前中后队列
  - 8.设计链表
  - 9.设计推特
- 其它
- - 1.链表组件
  - [2.找出临界点之间的最小和最大距离]

链表基础

链表的类型有三种：单链表、双链表、循环链表。

1.单链表：
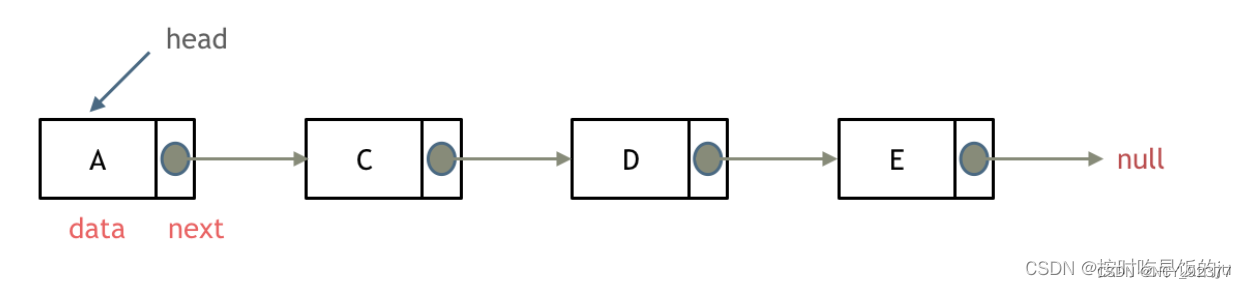
在这里插入图片描述

2.双链表：
在这里插入图片描述
3. 循环链表：

链表定义结构：

单链表

struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

循环链表

class Node {
public:
    int val;
    Node* next;

    Node() {}

    Node(int _val) {
        val = _val;
        next = NULL;
    }

    Node(int _val, Node* _next) {
        val = _val;
        next = _next;
    }
};

题型

一、单链表翻转、反转、旋转

1.反转链表

递归法：

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
		if (head == nullptr || head->next == nullptr) {
            return head;
        }
        ListNode* newHead = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return newHead;
    }
};

2.反转链表II——反转部分链表

牵针引线法：

class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        ListNode* dummyHead = new ListNode(-1);
        dummyHead->next = head;
        // pre指针指向旋转部分前的最后一个结点
        ListNode* pre = dummyHead;
        for (int i = 1; i < left; ++i) {
            pre = pre->next;
        }
        // curr指向已旋转部分完毕的最后一个结点
        ListNode* curr = pre->next;
        // next指向待插入的结点（也是curr的下一个结点）
        ListNode* next = curr->next;
        // 插入right-left次即可完成翻转
        for (int i = 0; i < right - left; ++i) {
            // cout << pre->val << " " << curr->val << " " << next->val << endl;
            curr->next = next->next;
            next->next = pre->next;
            pre->next = next;
            next = curr->next;
            
        }
        return dummyHead->next;
    }
};

需要存储三个变量：

pre指向待反转链表的前一个结点1（永远不变）
curr指向待反转链表的第一个结点2，也是已反转部分的最后一个结点（永远不变）
（例如需要反转ABCD，curr指向A结点，操作2次后已反转成CBAD，curr还是指向A结点，代表的是已反转部分的最后一个结点）
next指向待插入到已反转部分前面的结点（指向curr的下一个结点，由于curr的下一个节点会变化，所以每一次操作都需要更新）

第一次牵针引线（将结点3插入到pre结点之后）：

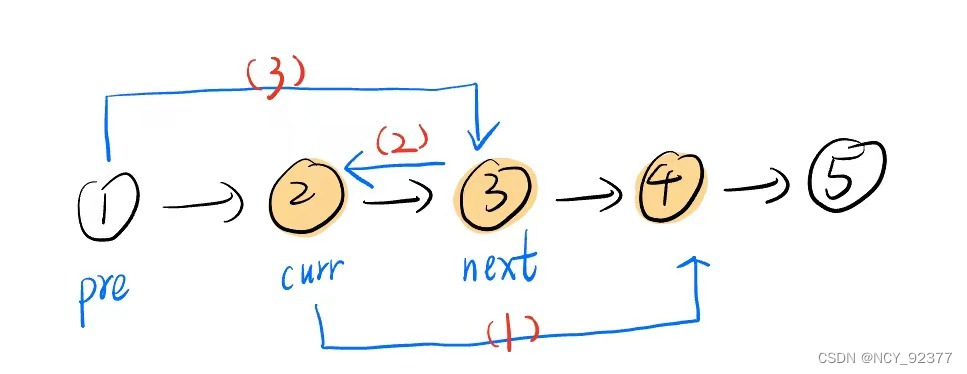
操作步骤(1)(2)(3)顺序不能改变：

(1) 将curr的下一个结点指向next的下一个结点curr->next = next->next;
(2) 将next的下一个结点指向pre的下一个结点（注意不是curr结点）next->next = pre->next;
(3) 将pre的下一个结点指向next结点 pre->next = next;

步骤(1)依赖于next的下一个结点，所以步骤(2)必须在步骤(1)之后；步骤(2)依赖于pre的下一个结点，所以步骤(3)必须(2)之后；

第二次牵针引线（将结点4插入到pre结点之后）：

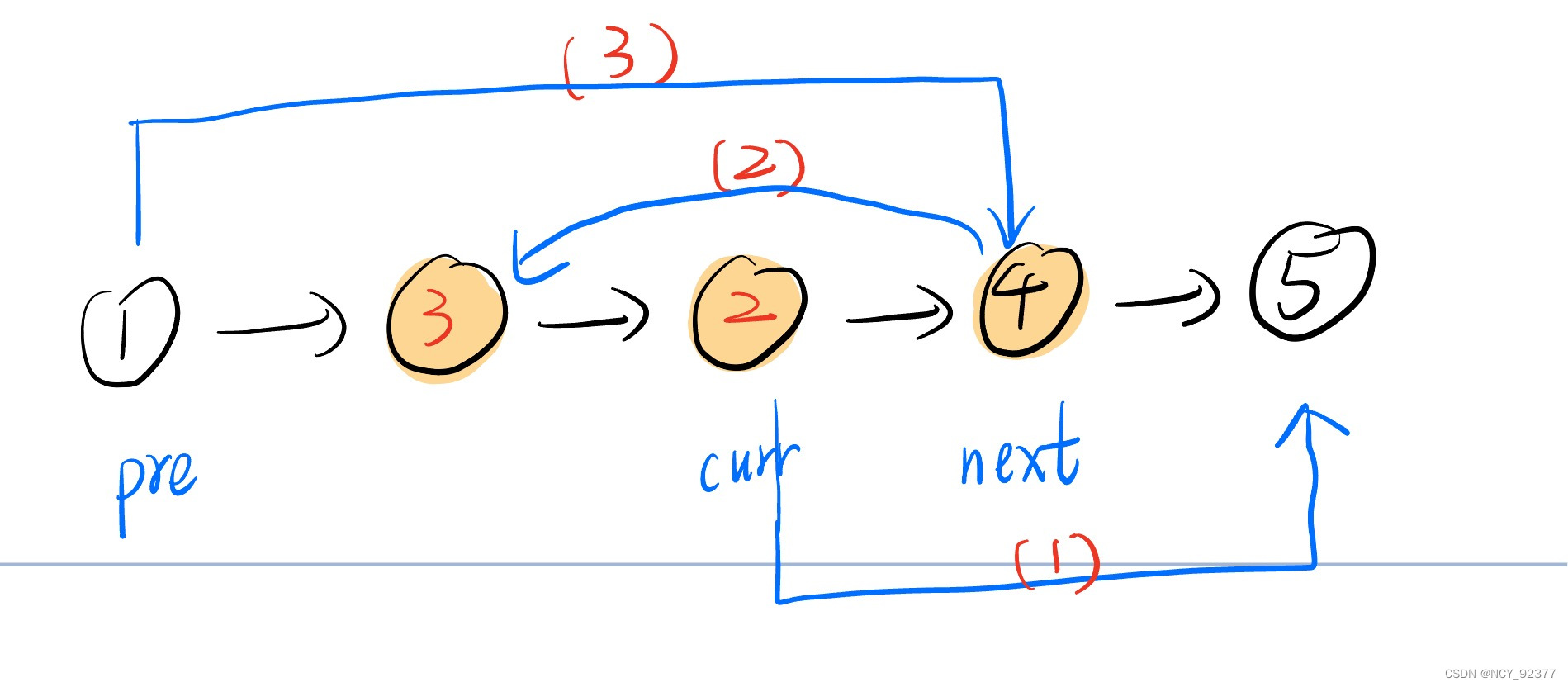
第二次插入完成后链表反转完成：1->4->3->2->5

总共需要right-left次“牵针引线”操作即可完成反转。

3.旋转链表

class Solution {
public:
    // n为链表长度，当k大于n时，k=k%n+1
    // 向右移动k位后，结点排列为前k个数为n-k+1到n；后n-k个数为1到n-k
    ListNode* rotateRight(ListNode* head, int k) {
        if (k == 0 || head == nullptr) { // *注意特殊情况
            return head;
        }        // 先遍历一遍获得链表长度
        ListNode* p = head;
        int n = 1;
        while (p->next != nullptr) {
            ++n;
            p = p->next;
        }
        k = k % n;
        // 构造循环链表
        p->next = head;
        // 将链表从n-k到n-k+1中间断开
        p = head;
        for (int i = 1; i < n - k; ++i, p = p->next) {} // p走到n-k结点 *注意p++和p=p->next不能替换
        ListNode* tmp = p;
        p = p->next;
        tmp->next = nullptr;
        return p;
    }
};

4.K个一组翻转链表

仍然是牵针引线，翻转k个结点，每组进行k-1次插入操作即可。翻转前，先判断是否至少还有k个节点剩余。

class Solution {
public:
    // 判断还有没有k个结点待反翻转
    bool canReverse(ListNode* p, int k) {
        int num = 0;
        while (p) {
            p = p->next;
            ++num;
            if (num >= k) {
                return true;
            }
        }
        return false;
    }

    ListNode* reverseKGroup(ListNode* head, int k) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }

        ListNode* dummyHead = new ListNode(-1, head);
        ListNode* pre = dummyHead;
        ListNode* curr = head;
        ListNode* next = curr->next;
        ListNode* p = pre;
        
        while (canReverse(p->next, k)) {
            int num = k - 1;
            while (num--) { // 插入k-1次即完成一组翻转
                curr->next = next->next;
                next->next = pre->next;
                pre->next = next;
                next = curr->next;
            }
            pre = curr;
            p = pre;
            if (next != nullptr) {
                curr = curr->next;
                next = next->next;
            } else {
                break;
            }
        }

        return dummyHead->next;
    }
};

5.反转偶数长度组的节点

class Solution {
public:
    ListNode* reverseEvenLengthGroups(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        ListNode* pre = head;
        ListNode* next;
        ListNode* p = head->next;
        int groupNum = 2;
        int curNum = 1;
        while (p && p->next) {
            while (p->next && curNum < groupNum) {
                p = p->next;
                ++curNum;
            }
            if (curNum % 2 == 0) {
                next = p->next;
                p->next = nullptr;
                ListNode* node = pre->next;
                pre->next = reverseList(pre->next);
                node->next = next;
                pre = node;
                p = pre->next;
            } else {
                pre = p;
                if (p) {
                    p = p->next;
                }
            }
            groupNum += 1;
            curNum = 1;
        }
        return head;
    }

    ListNode* reverseList(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        ListNode* newHead = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return newHead;
    }
};

二、删除单链表中的结点

1.删除链表的结点

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* deleteNode(ListNode* head, int val) {
        ListNode* dummyHead = new ListNode(-1);
        dummyHead->next = head;
        ListNode* p = dummyHead;
        while (p->next != nullptr) {
            if (p->next->val == val) {
                p->next = p->next->next;
                break;
            }
            p = p->next;
        }
        ListNode* res = dummyHead->next;
        delete dummyHead;
        return res;
    }
};

2.删除未排序链表中的重复节点

若要求空间复杂度O(n)，则可以使用哈希表存储每个元素是否出现。时间复杂度可达O(n)。

class Solution {
public:
    ListNode* removeDuplicateNodes(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        unordered_map<int, int> cnt;
        ListNode* p = head;
        cnt[head->val] = 1;
        while (p->next != nullptr) {
            if (cnt[p->next->val] > 0) { // 已经出现过的结点删除
                p->next = p->next->next;
            } else {
                cnt[p->next->val] = 1;
                p = p->next;
            }
        }
        return head;
    }
};

若要求空间复杂度O(1)，则只能以时间换空间，通过两重循环遍历实现，时间复杂度O(n^2）。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* removeDuplicateNodes(ListNode* head) {
        ListNode* p = head;
        while (p != nullptr) {
            ListNode* q = p;
            while (q->next != nullptr) {
                if (q->next->val == p->val) { // *注意写法：需要通过q->next的值与p的值比较，如果是比较q与p，则无法删除q节点（不知道前驱结点
                    q->next = q->next->next; // 删除q->next这个重复结点
                } else {
                    q = q->next;
                }
            }
            p = p->next;
        }
        return head;
    }
};

3.删除已排序链表中的重复元素I——重复元素只剩下一个

class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        ListNode* p = head->next; // 快指针
        ListNode* q = head; // 慢指针
        ListNode* res = q;
        while (p != nullptr) {
            if (p->val != q->val) {
                q->next = p;
                q = q->next;
            }
            p = p->next;
        }
        q->next = nullptr;
        return res;
    }
};

4.删除已排序链表中的重复元素II——重复元素全部删除

class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        ListNode* dummyHead = new ListNode(-101, head);
        ListNode* p = dummyHead;
        ListNode* q;
        while (p != nullptr && p->next != nullptr) {
            q = p->next->next;
            if (q && q->val == p->next->val) {
                // 找到下一个值不等于p->next值的节点q
                while (q && q->val == p->next->val) {
                    q = q->next;
                }
                p->next = q;
            } else {
                p = p->next;
            }
        }
        return dummyHead->next;
    }
};

5.删除链表的倒数第n个结点

方法一：先遍历一遍计算链表长度，再遍历第2遍删除倒数第n个结点

class Solution {
public:
    // 获取链表长度
    int getLength(ListNode* head) {
        int len = 0;
        while (head != nullptr) {
            ++len;
            head = head->next;
        }
        return len;
    }
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyHead = new ListNode(-1);
        dummyHead->next = head;
        int len = getLength(head);
        ListNode* p = dummyHead;
        // p走到倒数第n个结点的前驱结点
        for (int i = 1; i < len - n + 1; ++i) {
            p = p->next;
        }
        // 删除倒数第n个结点
        p->next = p->next->next;
        // 删除dummy节点，防止内存泄露
        ListNode* ans = dummyHead->next;
        delete dummyHead;
        return ans;
    }
}

方法二：使用快慢双指针，在快指针先走n+1步后慢指针再出发，当快指针到达链表尾部时，慢指针此时位于倒数第n个结点的前驱结点。

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        // 使用dummy头结点，防止头结点被删
        ListNode* dummyHead = new ListNode(-1, head);
        ListNode* fast = dummyHead;
        ListNode* slow = dummyHead;
        // 快指针先走n + 1个结点
        for (int i = 0; i <= n; ++i) {
            fast = fast->next;
        }
        // 快指针领先n + 1个结点后，快慢指针一起走，快指针走到nullptr时，慢指针正好指向倒数第n个结点的前驱结点
        while (fast != nullptr) {
            fast = fast->next;
            slow = slow->next;
        }
        // 删除倒数第n个结点
        slow->next = slow->next->next;
        // 删除dummy节点，防止内存泄露
        ListNode* ans = dummyHead->next;
        delete dummyHead;
        return ans;
    }
};

6.从链表中移除结点

对于列表中的每个节点 node ，如果其右侧存在一个具有严格更大值的节点，则移除 node。
提示：删除后应该是个单调非递增序列，每个结点的值都大于等于下一个结点的值。

方法一：递归操作

class Solution {
public:
    ListNode* removeNodes(ListNode* head) {
        if (head->next == nullptr) {
            return head;
        }
        ListNode* tmp = removeNodes(head->next); // tmp链表已是单调非递增序列
        // 比较head和tmp的值，head需要大于等于tmp才符合要求，否则将head删除
        if (head->val < tmp->val) { 
            return tmp; // 删除head
        }
        head->next = tmp; // head符合要求，加入到链表
        return head;
    }
};

方法二：反转思想。
容易推断最后一个结点一定是保留的，因为它后面不存在比它大的结点了，那么可以考虑将链表进行反转，从反转后的第一个结点开始，保留可以构成单调非递减序列的结点（后一个结点要大于等于前一个结点）。最后再将得到的链表反转一次就是结果了。
为什么需要逆序操作呢？因为可以确定最后一个结点一定保留，所以逆序只需要时间复杂度O(n)和空间复杂度O(1)；正序若不借助额外空间，则需要两重循环遍历才能完成。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        ListNode* newHead = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return newHead;
    }

    ListNode* removeNodes(ListNode* head) {
        head = reverseList(head);
        ListNode* p = head;
        int preVal = head->val;
        while (p->next != nullptr) {
            // cout << preVal << " " << p->next->val << endl;
            if (p->next->val < preVal) {
                p->next = p->next->next; // 删除p->next结点
            } else {
                preVal = p->next->val;
                p = p->next;
            }
        }
        return reverseList(head);
    }
};

7.删除链表的中间结点

删除第 ⌊n / 2⌋ 个节点（链表长度为n，下标从 0 开始）
⌊x⌋ 表示小于或等于 x 的最大整数。例如n=7，则删除下标为⌊7 / 2⌋ = 3的结点，也就是第4个结点。
当链表有奇数个结点时，删除中间的：

当链表有偶数个结点时，删除中间靠右的：

考虑使用快慢指针。从哑巴结点同时出发，快指针每次走两个结点，慢指针每次走一个结点，当快指针的下个结点或者下下个结点为nullptr时，慢指针刚好走到中间结点的前驱结点位置。

class Solution {
public:
    ListNode* deleteMiddle(ListNode* head) {
        ListNode* dummyHead = new ListNode(-1, head);
        if (head->next == nullptr) {
            return nullptr;
        }
        ListNode* fast = dummyHead;
        ListNode* slow = dummyHead;
        ListNode* pre = dummyHead;
        while (fast->next != nullptr && fast->next->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
        }
        slow->next = slow->next->next;
        ListNode* res = dummyHead->next;
        delete dummyHead;
        return res;
    }
};

8.从链表中删除总和值为零的连续节点

前缀和思想：记前缀和s[n]为前n个结点的值之和。假设0<i<j，则s[j] = s[i] + 连续区间(i,j]中结点的总和。若s[i]=s[j]，则说明连续区间(i,j]中结点的总和为0。
首先遍历一遍链表，记录每个前缀和最后出现的位置；第二遍遍历，如果发现当前结点i的前缀和记录的位置是j，则说明现了相同的前缀和，且这两个位置i和j之间的结点的值的总和是0，将这(i,j]的结点全部删除即可。
注意：除了两个结点的前缀和相等外，还有一种情况可以说明存在连续节点总和是0，那就是某个节点的前缀和为0的情况，例如s[i]=0，即前i个结点总和为0。可以考虑在头结点前设置一个哑巴头结点，将其值设置为0，那么其前缀和也是0，这样就能删除前i个结点了。

class Solution {
public:
    ListNode* removeZeroSumSublists(ListNode* head) {
        ListNode* dummyHead = new ListNode(0, head);
        // 第一遍遍历获取前缀和最后出现的结点位置
        unordered_map<int, ListNode*> last;
        ListNode* p = dummyHead;
        int sum = 0;
        while (p != nullptr) {
            sum += p->val;
            last[sum] = p;
            p = p->next;
        }
        // 第二遍遍历删除相同前缀和之间的结点
        p = dummyHead;
        sum = 0;
        while (p != nullptr) {
            sum += p->val;
            if (last[sum] != p) {
                // 删除(i,j]中的结点
                p->next = last[sum]->next;
            }
            p = p->next;
        }
        return dummyHead->next;
    }
};

9.删除链表中的结点

给定的是待删除的结点

由于是单链表，无法访问该节点的前驱结点，因此只能将当前结点置为后置结点的值，然后删除后置结点。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    void deleteNode(ListNode* node) {
        node->val = node->next->val;
        node->next = node->next->next;
    }
};

三、链表排序

1.单链表排序

常用的链表排序方法有堆排序、归并排序
- 堆排序：时间复杂度o(nlogn)、空间复杂度o(n)
- 归并排序：
  - 自顶向下排序：时间复杂度o(nlogn)、空间复杂度o(logn)
  - 自底向上排序：时间复杂度o(nlogn)、空间复杂度o(1)
  - 采用自底向上归并，可以把递归调用改为迭代，不使用额外空间。
方法一：堆排序

class Solution {
public:
    static bool cmp(ListNode* a, ListNode* b) {
        return a->val > b->val;
    }

    ListNode* sortList(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        priority_queue<ListNode*, vector<ListNode*>, decltype(&cmp)> heap(cmp); // 构造最小堆
        while (head != nullptr) {
            heap.push(head);
            head = head->next;
        }
        ListNode* dummyHead = new ListNode(-1);
        ListNode* p = dummyHead;
        while (!heap.empty()) {
            p->next = heap.top();
            heap.pop();
            p = p->next;
        }
        p->next = nullptr;
        return dummyHead->next;
    }
};

方法二：自顶向下的归并排序（递归实现）
- 步骤1：将链表从中间拆分成两个链表（使用快慢指针找中间结点）
- 步骤2：将两个链表分别进行排序（调用递归sortList）
- 步骤3：合并两个有序链表（merge）

class Solution {
public:
    ListNode* sortList(ListNode* head) {
        if (head == nullptr || head->next == nullptr) { // 空节点或单个节点不需要排序
            return head;
        }
        // 从中间将链表拆分成两部分分别进行排序，然后将两链表进行合并
        ListNode* mid = getMidNode(head);
        return merge(sortList(head), sortList(mid));
    }

    // 获取中间结点
    ListNode* getMidNode(ListNode* head) {
        ListNode* fast = head->next; // 相当于都从哑巴节点出发，快指针先走两步到head->next，慢指针走一步到head
        ListNode* slow = head;
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
        }
        ListNode* mid = slow->next;
        slow->next = nullptr; // 需要将前一段链表末尾置空
        return mid;
    }

    // 合并两个有序链表head1和head2为一个有序链表
    ListNode* merge(ListNode* head1, ListNode* head2) {
        // cout << head1->val << " " << head2->val << endl;
        ListNode* dummyHead = new ListNode(-1);
        ListNode* p = dummyHead;
        ListNode* p1 = head1;
        ListNode* p2 = head2;
        while (p1 && p2) {
            if (p1->val < p2->val) {
                p->next = p1;
                p1 = p1->next;
            } else {
                p->next = p2;
                p2 = p2->next;
            }
            p = p->next;
        }
        p->next = p1 ? p1 : p2;
        return dummyHead->next;
    }
};

方法三：自底向上的归并排序（迭代实现）

2.合并k个升序单链表

给定一个链表数组，每个链表都已经按升序排列。将所有链表合并成一个排序链表。

方法一：朴素的方法——先将链表1和链表2合并，然后合并后的链表和链表3合并，以此类推。

class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if (lists.empty()) {
            return nullptr;
        }
        ListNode* res = lists[0];
        for (int i = 1; i < lists.size(); ++i) {
            res = merge2Lists(lists[i], res);
        }
        return res;
    }

    ListNode* merge2Lists(ListNode* head1, ListNode* head2) {
        ListNode* dummyHead = new ListNode(-1);
        ListNode* p = dummyHead;
        while (head1 && head2) {
            if (head1->val < head2->val) {
                p->next = head1;
                head1 = head1->next;
            } else {
                p->next = head2;
                head2 = head2->next;
            }
            p = p->next;
        }
        p->next = head1 ? head1 : head2;
        return dummyHead->next;
    }
};

方法二：最小堆。将链表放入最小堆（优先队列），自动实现排序。

class Solution {
public:
    static bool cmp (ListNode* a, ListNode* b) {
        return a->val > b->val;
    }

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        priority_queue<ListNode*, vector<ListNode*>, decltype(&cmp)> heap(cmp);
        for (ListNode* p : lists) {
            while (p) {
                heap.push(p);
                p = p->next;
            }
        }
        ListNode* dummyHead = new ListNode(0);
        ListNode* p = dummyHead;
        while (!heap.empty()) {
            p->next = heap.top();
            cout << heap.top()->val << endl;
            heap.pop();
            p = p->next;
        }
        p->next = nullptr; // *最后一定要置空
        return dummyHead->next;
    }
};

方法三：归并排序

3.重排单链表

给定一个单链表 L 的头节点 head ，单链表 L 表示为：
```
L0 → L1 → … → Ln - 1 → Ln
```
请将其重新排列后变为：
```
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
```

将链表从中间分成两条链表，然后后半链表反转，再将两条链表进行合并。

class Solution {
public:
    void reorderList(ListNode* head) {
        if (!head || !head->next) {
            return;
        }
        ListNode* second = reverseList(splitFromMid(head));
        merge(head, second);
    }

    ListNode* splitFromMid(ListNode* head) {
        ListNode* fast = head->next;
        ListNode* slow = head;
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
        }
        ListNode* mid = slow->next;
        slow->next = nullptr;
        return mid;
    }

    ListNode* reverseList(ListNode* head) {
        if (!head || !head->next) {
            return head;
        }
        ListNode* newHead = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return newHead;
    }

    void merge(ListNode* head1, ListNode* head2) {
        ListNode* tmp;
        while (head1 && head2) {
            tmp = head2;
            head2 = head2->next;
            tmp->next = head1->next;
            head1->next = tmp;
            head1 = tmp->next;
        }
    }
};

4.排序的循环链表

给定循环单调非递减列表中的一个点，写一个函数向这个列表中插入一个新元素 insertVal ，使这个列表仍然是循环升序的

class Solution {
public:
    Node* insert(Node* head, int insertVal) {
        if (head == nullptr) {
            Node* node = new Node(insertVal);
            node->next = node;
            return node;
        }
        Node* p = head;
        bool begin = true;
        bool insert = false;
        while (p != head || begin) {
            if ((p->next->val < p->val && p->next->val > insertVal) || // 插入一个最小值
                (p->next->val < p->val && p->val < insertVal) ||       // 插入一个最大值
                (p->val <= insertVal && p->next->val >= insertVal)) {  // 插入一个中间值
                Node* node = new Node(insertVal);
                node->next = p->next;
                p->next = node;
                insert = true;
                break;
            }
            p = p->next;
            begin = false;
        }
        // 整个循环链表的值都相同
        if (!insert) {
            Node* node = new Node(insertVal);
            node->next = p->next;
            p->next = node;
        }
        return head;
    }
};

5.对单链表进行插入排序

插入排序算法的步骤:
1. 插入排序是迭代的，每次只移动一个元素，直到所有元素可以形成一个有序的输出列表。
2. 每次迭代中，插入排序只从输入数据中移除一个待排序的元素，找到它在序列中适当的位置，并将其插入。
3. 重复直到所有输入数据插入完为止。

class Solution {
public:
    ListNode* insertionSortList(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        
        ListNode* pre = new ListNode(5001, head); // 头结点前新增一个最大结点，保证该节点每次都在已排序链表的末尾
        ListNode* dummyHead = new ListNode(0, pre);
        ListNode* p = dummyHead;
        ListNode* curr = head;  // 待排序节点
        ListNode* next = curr->next;
        while (curr != nullptr) {
            next = curr->next;
            // p指向已排序链表中第一个值大于curr结点的前驱结点
            while (p != curr && p->next->val <= curr->val) {
                p = p->next;
            }
            // 将curr插入到p节点后
            curr->next = p->next;
            pre->next = next;
            p->next = curr;
            // 节点更新
            curr = next;           
            p = dummyHead;
        }
        deleteNode(dummyHead->next, pre);
        return dummyHead->next;
    }

    void deleteNode(ListNode* head, ListNode* node) {
        ListNode* p = head;
        while (p->next != node) {
            p = p->next;
        }
        p->next = p->next->next;
        delete node;
    }
};

四、回文链表

如果一个链表是回文，那么链表节点序列从前往后看和从后往前看是相同的。
在这里插入图片描述

1.判断回文链表

回文链表一定是对称的，所以从中间结点分割链表，然后将后面的链表反转，再比较两条链表是否一致。

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return true;
        }
        if (head->next->next == nullptr) {
            return head->val == head->next->val;
        }
        ListNode* second = reverseList(splitFromMid(head));
        while (head && second) {
            if (head->val != second->val) {
                return false;
            }
            head = head->next;
            second = second->next;
        }
        return true;
    }

    ListNode* splitFromMid(ListNode* head) {
        ListNode* fast = head->next; // fast和slow别写放反
        ListNode* slow = head;
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
        }
        ListNode* mid = slow->next;
        slow->next = nullptr;
        return mid;
    }

    ListNode* reverseList(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        ListNode* newHead = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return newHead;
    }
};

五、环形链表

1.判断环形链表：判断链表中是否存在环，如图：链表尾部结点连接到了链表中间结点。

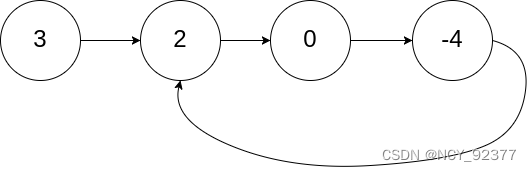
使用快慢指针判断链表中是否存在环。快指针每次走两步，慢指针每次走一步。当快慢指针都再环中移动时，由于快指针速度快，所以快指针一定能追上慢指针，也就是快慢指针相遇则说明存在环。
当两个指针都进入环后，每轮移动使得慢指针到快指针的距离增加一，同时快指针到慢指针的距离也减少一，只要一直移动下去，快指针总会追上慢指针。
如果链表存在环，则链表末尾不存在nullptr.

class Solution {
public:
    bool hasCycle(ListNode *head) {
        if (head == nullptr || head->next == nullptr) {
            return false;
        }
        ListNode* fast = head->next;
        ListNode* slow = head;
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) {
                return true;
            }
        }
        return false;
    }
};

2.环形链表II：返回链表开始入环的第一个节点。如果链表无环，则返回 null。

仍然使用快慢指针，快指针每次走两步，慢指针每次走一步。
如图：假设头结点到入环点的距离为a步，慢指针在环内走了b步后两指针相遇（假设在快指针在环内走了n圈），相遇点继续走到入环点距离为c步。
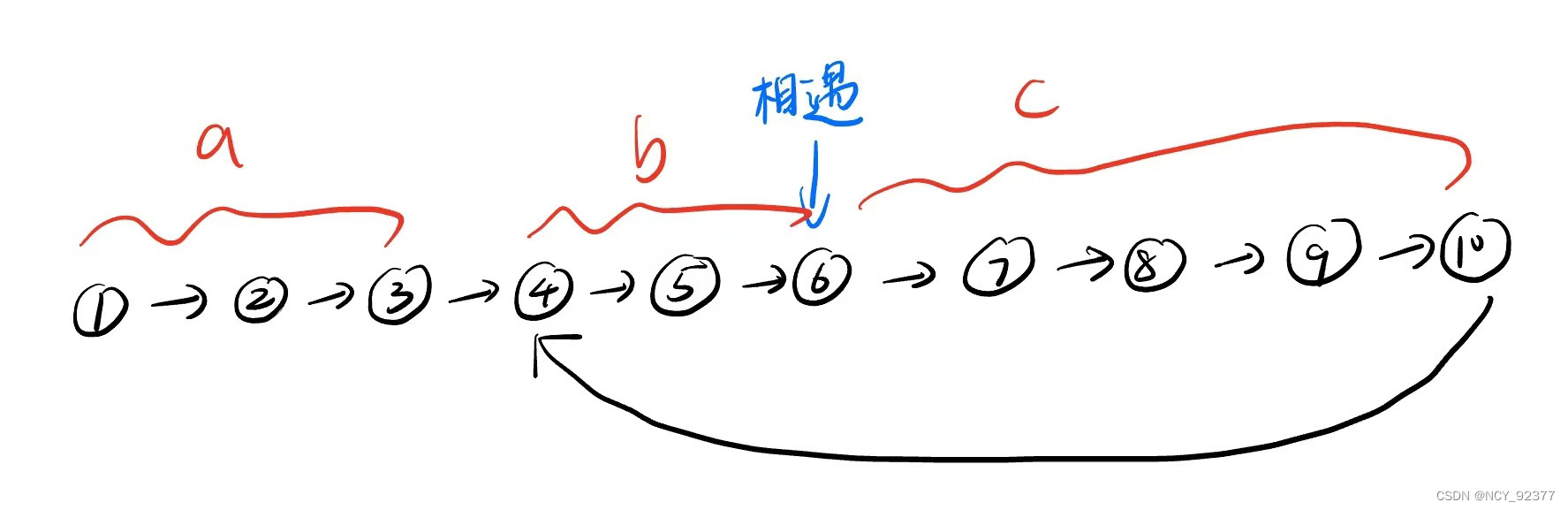
可知快慢指针相遇时，慢指针走了a+b步，快指针走了a+b+n(b+c)步，由于快指针速度是慢指针的两倍，所以快指针走的步数一定是慢指针的两倍，解方程a+b=a+n(b+c)+b可得a=n(b+c)-b=(n-1)(b+c)+c。
这个方程说明当一个指针从头结点出发，同时慢指针从相遇点出发，他们第一次相遇一定会在入环点。
注意fast和slow都从head结点出发，这里统计的是步数，如果两者从dummyHead出发（即fast先走到head->next，slow走到head），那么结论就不正确了。

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (head == nullptr || head->next == nullptr) {
            return nullptr;
        }
        ListNode* fast = head; // *注意不是head->next
        ListNode* slow = head;
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) {
                cout << fast->val << endl;
                ListNode* p = head;
                while (p != slow) {
                    p = p->next;
                    slow = slow->next;
                }
                return p;
            }
        }
        return nullptr;
    }
};

六、获取链表结点

1.返回倒数第k个节点

快慢指针

class Solution {
public:
    int kthToLast(ListNode* head, int k) {        
        ListNode* fast = head;
        int num = k;
        while (num--) {
            fast = fast->next;
        }
        ListNode* slow = head;
        while (fast) {
            fast = fast->next;
            slow = slow->next;
        }
        return slow->val;
    }
};

返回链表中倒数第k个结点

同上，这里返回结点。

class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {        
        ListNode* fast = head;
        int num = k;
        while (num--) {
            fast = fast->next;
        }
        ListNode* slow = head;
        while (fast) {
            fast = fast->next;
            slow = slow->next;
        }
        return slow;
    }
};

链表的中间节点：给你单链表的头结点 head ，请你找出并返回链表的中间结点。如果有两个中间结点，则返回第二个中间结点。

class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
        }
        return slow;
    }
};

链表随机结点

class Solution {
public:
    Solution(ListNode* head) {
        while (head) {
            arr.push_back(head->val);
            head = head->next;
        }
    }
    
    int getRandom() {
        return arr[rand() % arr.size()];
    }

private:
    vector<int> arr;
};

5.交换链表节点

交换链表正数第 k 个节点和倒数第 k 个节点的值后，返回链表的头节点（链表从 1 开始索引）。

交换结点的值即可，无需交换结点。

class Solution {
public:
    ListNode* swapNodes(ListNode* head, int k) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        ListNode* kNode = head;
        for (int i = 1; i < k; ++i) {
            kNode = kNode->next;
        }
        ListNode* lastKNode = findLastKNode(head, k);
        int tmp = kNode->val;
        kNode->val = lastKNode->val;
        lastKNode->val = tmp;
        return head;
    }

    ListNode* findLastKNode(ListNode* head, int k) {
        ListNode* fast = head;
        for (int i = 1; i <= k; ++i) {
            fast = fast->next;
        }
        ListNode* slow = head;
        while (fast) {
            fast = fast->next;
            slow = slow->next;
        }
        return slow;
    }
};

七、链表相交

两个链表的第一个重合节点：如图c1为第一个重合节点，若没有重合节点返回nullptr。

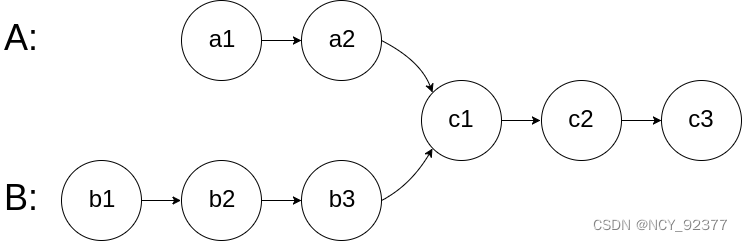
在这里插入图片描述

方法一：哈希表。判断两个链表是否相交，可以使用哈希集合存储链表节点。首先遍历链表1，并将链表1中的每个节点加入哈希集合中。然后遍历链表2对于遍历到的每个节点，判断该节点是否在哈希集合中。

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        unordered_set<ListNode*> nodeSet;
        while (headA) {
            nodeSet.insert(headA);
            headA = headA->next;
        }
        while (headB) {
            if (nodeSet.find(headB) != nodeSet.end()) {
                return headB;
            }
            headB = headB->next;
        }
        return nullptr;
    }
};

方法二：双指针。两个指针分别从两个链表头结点出发，当指针走到链表结尾时下一步就到另一条链表的头结点开始遍历。假设链表1在相交前长a，链表2在相交前长b，相交部分长度为c。两个指针在走完自身链表后又分别走了对方链表不相交的部分，即两个指针都在走了a+b+c的距离时刚好相交点相遇。如果两个链表不相交，则它们会同时指向nullptr。

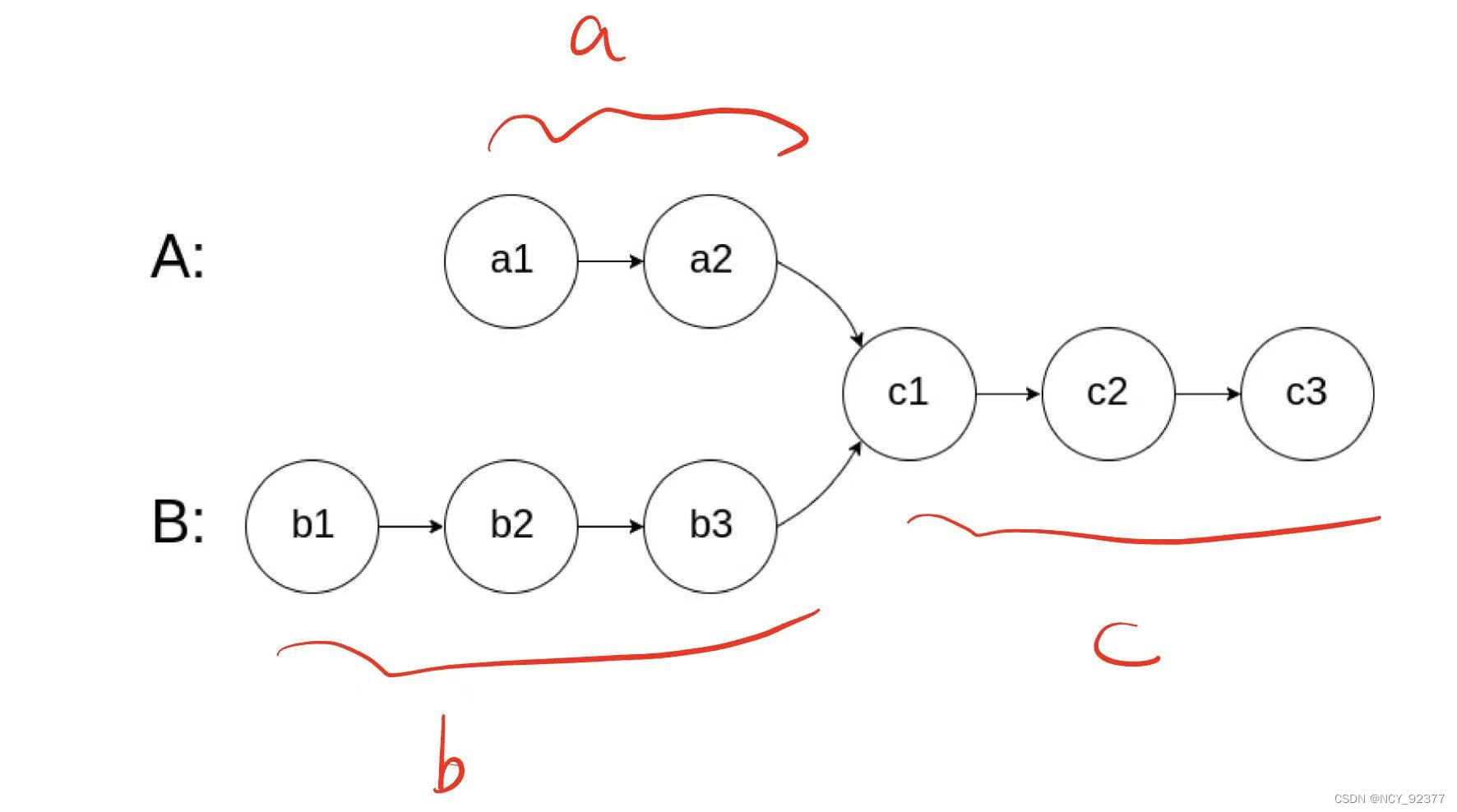
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* pA = headA;
        ListNode* pB = headB;
        while (pA != pB) {
            pA = pA ? pA->next : headB;
            pB = pB ? pB->next : headA;
        }
        return pA;
    }
};

八、链表合并

合并零之间的结点

class Solution {
public:
    ListNode* mergeNodes(ListNode* head) {
        ListNode* dummyHead = new ListNode(-1);
        ListNode* p = dummyHead;
        int tmp = 0;
        head = head->next;
        while (head != nullptr) {
            if (head->val != 0) {
                tmp += head->val;
            } else {
                ListNode* node = new ListNode(tmp);
                p->next = node;
                p = p->next;
                tmp = 0;
            }
            head = head->next;
        }
        return dummyHead->next;
    }
};

合并两个链表

class Solution {
public:
    ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {
        ListNode* dummyHead = new ListNode(-1, list1);
        // 找到a前驱节点
        ListNode* pre = dummyHead;
        for (int i = 0; i < a; ++i) {
            pre = pre->next;
        }
        //找到b后继结点
        ListNode* next = pre->next;
        for (int i = a; i <= b; ++i) {
            next = next->next;
        }
        // 合并
        pre->next = list2;
        while (list2->next) {
            list2 = list2->next;
        }
        list2->next = next;
        return dummyHead->next;
    }
};

九、链表的计算

1.两数相加II

给你两个非空链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        l1 = reverseList(l1);
        l2 = reverseList(l2);
        ListNode* res = new ListNode(0);
        ListNode* p = res;
        int c = 0;
        while (l1 && l2) {
            ListNode* node = new ListNode((c + l1->val + l2->val) % 10);
            c = (c + l1->val + l2->val) / 10;
            p->next = node;
            p = p->next;
            l1 = l1->next;
            l2 = l2->next;               
        }
        p->next = l1 ? l1 : l2;
        while (l1) {
            int v = l1->val;
            l1->val = (v + c) % 10;
            c = (v + c) / 10;
            l1 = l1->next;
            p = p->next;
        }
        while (l2) {
            int v = l2->val;
            l2->val = (v + c) % 10;
            c = (v + c) / 10;
            l2 = l2->next;
            p = p->next;
        }
        if (c != 0) {
            ListNode* node = new ListNode(c);
            p->next = node;
            node->next = nullptr;
        }
        return reverseList(res->next);
    }

    ListNode* reverseList(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        ListNode* newHead = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return newHead;
    }
};

3.链表最大孪生和

链表拆分+链表反转

class Solution {
public:
    int pairSum(ListNode* head) {
        ListNode* mid = reverseList(split(head));
        int maxSum = 0;
        while (head && mid) {
            maxSum = max(maxSum, head->val + mid->val);
            head = head->next;
            mid = mid->next;
        }
        return maxSum;
    }

    ListNode* split(ListNode* head) {
        ListNode* fast = head->next;
        ListNode* slow = head;
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
        }
        ListNode* mid = slow->next;
        slow->next = nullptr;
        return mid;
    }

    ListNode* reverseList(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
             return head;
        }
        ListNode* newHead = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return newHead;
    }
};

4.二进制链表转整数

二进制转换方式：
虽然每一位乘以2的次方数与位数有关，但是不必知道总位数（链表长度），只需要每次将当前结点当做是最低位数（即当前节点值乘以2的0次方），然后在读到下一个节点值的时候，将已经读到的结果乘以2即可（是一样的结果）。

class Solution {
public:
    int getDecimalValue(ListNode* head) {
        int res = 0;
        int num = 0;
        while (head) {
            res = res * 2 + head->val;
            head = head->next;
        }
        return res;
    }
};

十、分割链表

1.分割链表

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有小于 x 的节点都出现在大于或等于 x 的节点之前。

class Solution {
public:
    ListNode* partition(ListNode* head, int x) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        ListNode* dummyHead = new ListNode(-1, head);
        ListNode* pre = dummyHead;
        ListNode* curr = dummyHead;
        while (curr && curr->next) {
            if (curr->next->val < x && pre != curr) {
                // 将curr->next插入到pre后面
                ListNode* next = curr->next->next;
                curr->next->next = pre->next;
                pre->next = curr->next;
                curr->next = next;
                // 更新节点
                pre = pre->next;
            } else {
                curr = curr->next;
            }
        }
        return dummyHead->next;
    }
};

2.分隔链表

给你一个头结点为 head 的单链表和一个整数 k ，请你设计一个算法将链表分隔为 k 个连续的部分。每部分的长度应该尽可能的相等：任意两部分的长度差距不能超过 1 。这可能会导致有些部分为 null 。这 k 个部分应该按照在链表中出现的顺序排列，并且排在前面的部分的长度应该大于或等于排在后面的长度。
返回一个由上述 k 部分组成的数组。

穿针引线

class Solution {
public:
    ListNode* oddEvenList(ListNode* head) {
        ListNode* pre = head;
        ListNode* curr = head;
        ListNode* next;
        int num = 2;
        while (curr && curr->next) {
            if (num % 2 == 1) {
                // curr->next结点放到pre节点后
                next = curr->next->next;
                curr->next->next = pre->next;
                pre->next = curr->next;
                curr->next = next;
                // 更新节点
                curr = next;
                pre = pre->next;
                // curr移动到next，移动了两个结点
                num += 2; 
            } else {
                curr = curr->next;
                num += 1;
            }
        }
        return head;
    }
};

链表与二叉树

1.BiNode

二叉树数据结构TreeNode可用来表示单向链表（其中left置空，right为下一个链表节点）。实现一个方法，把二叉搜索树转换为单向链表，要求依然符合二叉搜索树的性质，转换操作应是原址的，也就是在原始的二叉搜索树上直接修改。
返回转换后的单向链表的头节点。

可以通过中序遍历获得从小到大顺序的二叉搜索树结点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* convertBiNode(TreeNode* root) {
        inOrder(root);
        return head->right;
    }

    void inOrder(TreeNode* root) {
        if (root == nullptr) {
            return;
        }
        inOrder(root->left);
        pre->right = root;
        root->left = nullptr;
        pre = root;
        inOrder(root->right);
    }

private:
    TreeNode* head = new TreeNode(-1);
    TreeNode* pre = head;
};

2.特定深度结点链表

给定一棵二叉树，设计一个算法，创建含有某一深度上所有节点的链表（比如，若一棵树的深度为 D，则会创建出 D 个链表）。返回一个包含所有深度的链表的数组。

利用队列进行层序遍历。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    vector<ListNode*> listOfDepth(TreeNode* tree) {
        if (tree == nullptr) {
            return {};
        }
        vector<ListNode*> res;
        res.push_back(new ListNode(tree->val));
        queue<TreeNode*> q;
        q.push(tree);
        while (!q.empty()) {
            ListNode* dummyHead = new ListNode(-1);
            ListNode* p = dummyHead;
            int len = q.size();
            while (len--) {
                auto top = q.front();
                q.pop();
                if (top->left) {
                    p->next = new ListNode(top->left->val);
                    p = p->next;
                    q.push(top->left);
                }
                if (top->right) {
                    p->next = new ListNode(top->right->val);
                    p = p->next;
                    q.push(top->right);
                }
            }
            p->next = nullptr;
            if (dummyHead->next) {
                res.push_back(dummyHead->next);
            }
        }
        return res;
    }
};

3.二叉树中的链表

两个递归。一个枚举起点，一个用于判断从该起点出发能否匹配链表。

Solution {
public:
    bool isSubPath(ListNode* head, TreeNode* root) {
        if (root == nullptr) {
            return false;
        }
        return dfs(head, root) || isSubPath(head, root->left) || isSubPath(head, root->right); // 枚举起点
    }

    bool dfs(ListNode* head, TreeNode* root) {
        if (head == nullptr) {
            return true;
        }
        if (root == nullptr) {
            return false;
        }
        if (head->val != root->val) {
            return false;
        }
        return dfs(head->next, root->left) || dfs(head->next, root->right);
    }
};

4.填充每个结点的下一个右侧节点指针

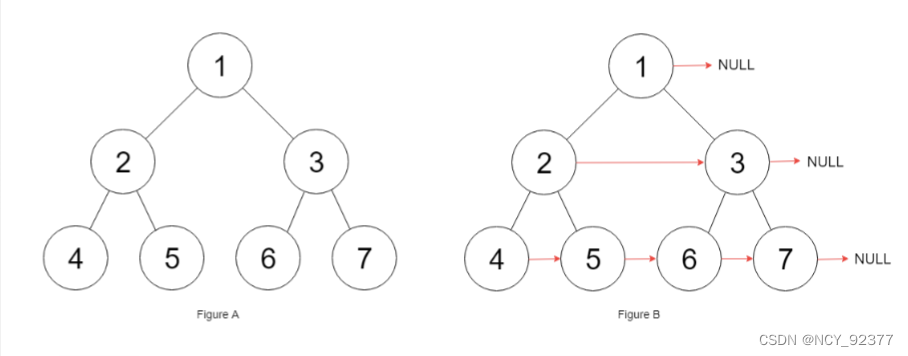
中序遍历

class Solution {
public:
    Node* connect(Node* root) {
        if (root == nullptr) {
            return root;
        }
        queue<Node*> q;
        q.push(root);
        Node* dummyHead = new Node(-1);
        Node* p = dummyHead;
        while (!q.empty()) {
            p = dummyHead;
            int len = q.size();
            while (len--) {
                Node* top = q.front();
                q.pop();
                if (top->left) {
                    p->next = top->left;
                    p = p->next;
                    q.push(top->left);
                }
                if (top->right) {
                    p->next = top->right;
                    p = p->next;
                    q.push(top->right);
                }
            }
        }
        delete dummyHead;
        return root;
    }
};

5.二叉树展开为链表

用先序遍历。由于将二叉树展开为链表之后会破坏二叉树的结构，因此在前序遍历过程中记录顺序，遍历完成后再更新左右结点指针的信息。

class Solution {
public:
    void flatten(TreeNode* root) {
        if (root == nullptr) {
            return;
        }
        vector<TreeNode*> orderList;
        preOrder(root, orderList);
        for (int i = 1; i < orderList.size(); ++i) {
            root->right = orderList[i];
            root->left = nullptr;
            root = root->right;
        }
    }

    // 先序遍历：根->左->右    
    void preOrder(TreeNode* root, vector<TreeNode*>& orderList) {
        if (root == nullptr) {
            return;
        }
        orderList.push_back(root);
        preOrder(root->left, orderList);
        preOrder(root->right, orderList);
    }
};

6.有序链表转化平衡二叉搜索树

通过链表解题

1.使数组按非递减顺序排列——链表+单调栈

链表的复制

1.复杂链表的复制

因为复杂链表包含一个随机指针，在创建当前节点时，该随机指针指向的节点不一定创建好了。所以可以构造新旧链表结点之间的映射mp，mp[newNode]=oldNode，mp[oldNode]=newNode，第一次遍历旧链表构造新节点（包括val和next指针）以及映射；第二次遍历新链表，通过mp[mp[newNode]->random]获取到该结点的随机指针应该指向的另一个新节点。

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/
class Solution {
public:
    Node* copyRandomList(Node* head) {
        // 构建新旧链表节点之间的哈希映射
        unordered_map<Node*, Node*> mp;
        Node* newList = new Node(-1);
        Node* p = head;
        Node* q = newList;
        while (p) {
            // 建立新链表
            Node* node = new Node(p->val);
            q->next = node;
            q = q->next;
            // 构建映射
            mp[p] = node;
            mp[node] = p;
            p = p->next;
        }
        q->next = nullptr;
        q = newList->next;
        while (q) {
            q->random = mp[mp[q]->random];
            q = q->next;
        }
        return newList->next;
    }
};

双向链表

1.扁平化多级双向链表

递归处理

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* prev;
    Node* next;
    Node* child;
};
*/

class Solution {
public:
    Node* flatten(Node* head) {
        if (head == nullptr) {
            return head;
        }
        dfs(head);
        return head;
    }

    Node* dfs(Node* head) {
        if (head->child == nullptr && head->next == nullptr) {
            return head;
        }
        if (head->child) {
            Node* next = head->next;
            head->next = head->child;
            head->child->prev = head;
            Node* tail = dfs(head->child);
            head->child = nullptr;
            tail->next = next;
            if (next) {
                next->prev = tail;
            }
        }
        return dfs(head->next);
    }
};

2.二叉搜索树与双向循环链表

中序遍历

class Solution {
public:
    Node* treeToDoublyList(Node* root) {
        if (root == nullptr) {
            return root;
        }
        inOrder(root);
        pre->right = dummyHead->right;
        dummyHead->right->left = pre;
        return dummyHead->right;
    }

    // 中序遍历：左->根->右
    void inOrder(Node* root) {
        if (root == nullptr) {
            return;
        }
        inOrder(root->left);
        pre->right = root;
        root->left = pre;
        pre = root;
        inOrder(root->right);
    }

private:
    Node* dummyHead = new Node(-1);
    Node* pre = dummyHead;
};

链表设计题

1.设计哈希集合

2.LRU缓存

题意： 实现LRU：Least Recent Used，即最近最少使用算法。

get函数：如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1
push函数：如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该逐出最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

解题思路：

由于get和put操作设计查找和插入，两者都需要满足O(1)的时间复杂度，因此可以通过哈希表+双向链表实现。

哈希表——存储key和链表结点的映射。实现由key到value的快速查找，复杂度o(1)。
双向链表——存储每个结点的最近访问顺序，结点保存key和value信息，结点的顺序就是最近有访问的排在前面，最后的结点是最近最久未访问的结点。实现快速插入删除结点。

算法思想

每次get时，判断key值在哈希表中是否存在
- 若不存在，返回-1；
- 若存在，首先将该结点移动至链表前面，然后通过哈希访问该节点的值。
每次put时，判断key值在哈希表中是否存在
- 若存在，将该节点移动之链表前面，并通过哈希访问该节点更新value的值。
- 若不存在，则新建一个key结点，并插入到队列前面，同时建立哈希映射关系。如果插入该节点后，结点数超过容量，则需要将链表的最后一个节点移除，同时删除其哈希映射关系。

具体实现

定义双向链表：节点要包含key，value，prev指针和next指针。
（不能只有value，还必须包含key，因为删除最后一个节点的哈希映射关系时需要用到key）
定义双向链表头指针head——方便插入操作；尾指针tail——方便删除操作。

// 双向链表
struct DListNode {
    int key;
    int val;
    DListNode* prev;
    DListNode* next;
    DListNode() : key(0), val(0), prev(nullptr), next(nullptr) {}
    DListNode(int key_, int val_) : key(key_), val(val_), prev(nullptr), next(nullptr) {}
};

class LRUCache {
public:
    LRUCache(int capacity) {
        this->capacity = capacity;
        head->next = tail;
        tail->prev = head;
    }
    
    int get(int key) {
        if (mp.count(key) == 0) {
            return -1;
        }
        // 将访问的该节点移动到头部
        removeToHead(mp[key]);
        return mp[key]->val;
    }
    
    void put(int key, int value) {
        if (!mp.count(key)) {
            // 新建节点插入到链表头部
            DListNode* node = insertToHead(key, value);
            mp[key] = node;          
            ++size;
            if (size > capacity) {
                // 移除最近最久未使用的结点
                node = removeLastNode();
                mp.erase(node->key);
                --size;
            }
        } else {
            mp[key]->val = value;
            removeToHead(mp[key]); // 因为访问了该结点，所以移动到链表头部
        }
    }

protected:
    // 插入节点到链表头部
    DListNode* insertToHead(int key, int val) {
        DListNode* node = new DListNode(key, val);
        node->next = head->next;
        head->next = node;
        node->prev = head;
        node->next->prev = node;
        return node;
    }

    // 逐出最近最久未使用的节点（即链表的最后一个节点）
    DListNode* removeLastNode() {
        DListNode* node = tail->prev;
        node->prev->next = tail;
        tail->prev = node->prev;
        return node;
    }

    // 将某结点移动到链表头部
    void removeToHead(DListNode* node) {
        // 将node前后结点进行连接
        node->prev->next = node->next;
        node->next->prev = node->prev;
        // 将node插入head之后
        node->next = head->next;
        head->next = node;
        node->prev = head;
        node->next->prev = node;
    }

private:
    int capacity {0};
    int size {0};
    unordered_map<int, DListNode*> mp;
    DListNode* head = new DListNode(); // 双向链表头结点
    DListNode* tail = new DListNode(); // 双向链表尾节点
};

另外，打印输出也会占用时间诶，看来不能瞎搞QaQ

3.LFU缓存

最不经常使用（LFU）算法和最近最久未使用（LRU）算法，都是内存管理的页面置换算法，它们的区别是：

LRU，即：最近最少使用淘汰算法（Least Recently Used）。LRU是淘汰最长时间没有被使用的页面。
LRU关键是看数据最后一次被使用到发生替换的时间长短，时间越长，数据就会被置换；
LFU，即：最不经常使用淘汰算法（Least Frequently Used）。LFU是淘汰一段时间内，使用次数最少的页面。
LFU关键是看一定时间段内页面被使用的频率（次数），使用频率越低，数据就会被置换。

解题思路：

为了确定最不常使用的键，可以为缓存中的每个键维护一个使用计数器cnt 。使用计数最小的键是最久未使用的键。当一个键首次插入到缓存中时，它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作，使用计数器的值将会递增。

4.设计浏览器缓存

双向链表实现。curr指针指向当前访问的页面，每次visit在链表后面增加接地那，back时链表通过prev指针遍历，forward时链表通过next指针遍历。

struct DListNode {
    string url;
    DListNode* prev;
    DListNode* next;
    DListNode() : url(""), prev(nullptr), next(nullptr) {}
    DListNode(string url_) : url(url_), prev(nullptr), next(nullptr) {}
};

class BrowserHistory {
public:
    BrowserHistory(string homepage) {
        head->url = homepage;
    }
    
    void visit(string url) {
        DListNode* node = new DListNode(url);
        curr->next = node;
        node->prev = curr;
        curr = node;
    }
    
    string back(int steps) {
        while (curr->prev && steps--) {
            curr = curr->prev;
        }
        return curr->url;
    }
    
    string forward(int steps) {
        while (curr->next && steps--) {
            curr = curr->next;
        }
        return curr->url;
    }

private:
    DListNode* head = new DListNode();
    DListNode* curr = head;
};

5.设计循环队列

链表实现。定义头指针head和尾指针tail，这里两者是链表真正的头结点和尾节点，初始head和tail都置空。
队列需满足先入先出条件，所以从尾部插入结点，从头部删除结点。
使用size和capacity判断是否为空和是否满队列

class MyCircularQueue {
public:
    MyCircularQueue(int k) {
        capacity = k;
        head = tail = nullptr;
    }
    
    bool enQueue(int value) {
        if (isFull()) {
            return false;
        }
        ListNode* node = new ListNode(value);
        if (head) {
            // 从尾部插入
            tail->next = node;
            tail = node;
        } else {
            head = tail = node;
        }
        ++size;
        return true;
    }
    
    bool deQueue() {
        if (isEmpty()) {
            return false;
        }
        // 从头部删除
        ListNode* node = head;
        head = head->next;
        delete node;
        --size;
        return true;
    }
    
    int Front() {
        return isEmpty() ? -1 : head->val;
    }
    
    int Rear() {
        return isEmpty() ? -1 : tail->val;
    }
    
    bool isEmpty() {
        return size == 0;
    }
    
    bool isFull() {
        return size == capacity;
    }

private:
    int size {0};
    int capacity {0};
    ListNode* head;
    ListNode* tail;
};

6.设计循环双端队列

双向链表实现

struct DListNode {
    int val;
    DListNode* prev;
    DListNode* next;
    DListNode() : val(0), prev(nullptr), next(nullptr) {}
    DListNode(int val_) : val(val_), prev(nullptr), next(nullptr) {}
};

class MyCircularDeque {
public:
    MyCircularDeque(int k) {
        capacity = k;
        head->next = tail;
        tail->prev = head;
    }
    
    bool insertFront(int value) {
        if (size >= capacity) {
            return false;
        }
        // head前面添加node节点，head的值置为value，head前移一位
        DListNode* node = new DListNode();
        node->next = head;
        head->prev = node;
        head->val = value;
        head = head->prev;
        ++size;
        return true;
    }
    
    bool insertLast(int value) {
        if (size >= capacity) {
            return false;
        }
        // tail后添加node节点，tail的值置为value，tail后移一位
        DListNode* node = new DListNode();
        tail->next = node;
        node->prev = tail;
        tail->val = value;
        tail = tail->next;
        ++size;
        return true;
    }
    
    bool deleteFront() {
        if (size <= 0) {
            return false;
        }
        DListNode* node = head->next;
        head->next = node->next;
        node->next->prev = head;
        delete node;
        --size;
        return true;
    }
    
    bool deleteLast() {
        if (size <= 0) {
            return false;
        }
        DListNode* node = tail->prev;
        node->prev->next = tail;
        tail->prev = node->prev;
        delete node;
        --size;
        return true;
    }
    
    int getFront() {
        return size <= 0 ? -1 : head->next->val;
    }
    
    int getRear() {
        return size <= 0 ? -1 : tail->prev->val;
    }
    
    bool isEmpty() {
        return size == 0;
    }
    
    bool isFull() {
        return size == capacity;
    }

private:
    DListNode* head = new DListNode();
    DListNode* tail = new DListNode();
    int capacity {0};
    int size {0};
};

7.设计前中后队列

双向链表实现

struct DListNode {
    int val;
    DListNode* prev;
    DListNode* next;
    DListNode() : val(0), prev(nullptr), next(nullptr) {}
    DListNode(int val_) : val(val_), prev(nullptr), next(nullptr) {}
};

class FrontMiddleBackQueue {
public:
    FrontMiddleBackQueue() {
        head->next = tail;
        tail->prev = head;
    }
    
    void pushFront(int val) {
        DListNode* node = new DListNode();
        node->next = head;
        head->prev = node;
        head->val = val;
        head = head->prev;
        ++size;
    }

    void pushMiddle(int val) {
        DListNode* mid = getMidNode();
        DListNode* node = new DListNode(val);
        if (size % 2 == 1) { // 期数个结点在mid前插入
            mid->prev->next = node;
            node->prev = mid->prev;
            node->next = mid;
            mid->prev = node;
        } else { // 偶数个结点在mid后插入
            node->next = mid->next;
            mid->next->prev = node;
            mid->next = node;
            node->prev = mid;
        }
        ++size;
    }
    
    void pushBack(int val) {
        DListNode* node = new DListNode();
        tail->next = node;
        node->prev = tail;
        tail->val = val;
        tail = tail->next;
        ++size;
    }
    
    int popFront() {
        if (size <= 0) {
            return -1;
        }
        int res = head->next->val;
        DListNode* node = head->next;
        head->next = node->next;
        node->next->prev = head;
        delete node;
        --size;
        return res;
    }

    int popMiddle() {
        if (size <= 0) {
            return -1;
        }
        DListNode* mid = getMidNode();
        mid->prev->next = mid->next;
        mid->next->prev = mid->prev;
        int res = mid->val;
        delete mid;
        --size;
        return res;
    }
    
    int popBack() {
        if (size <= 0) {
            return -1;
        }
        int res = tail->prev->val;
        DListNode* node = tail->prev;
        node->prev->next = tail;
        tail->prev = node->prev;
        delete node;
        --size;
        return res;
    }

protected:
    // 1 2 (3) 4 5
    // 1 2 (3) 4 5 6
    DListNode* getMidNode() {
        DListNode* p = head;
        for (int i = 1; i <= size / 2; ++i) {
            p = p->next;
        }
        if (size % 2 == 1) {
            p = p->next;
        }
        return p;
    }

private:
    int size {0};
    DListNode* head = new DListNode();
    DListNode* tail = new DListNode();
};

8.设计链表

使用head和tail指针作为虚拟头结点和尾节点，方便两端插入操作

class MyLinkedList {
public:
    MyLinkedList() {
        size = 0;
        head = new ListNode();
        tail = new ListNode();
        head->next = tail;
    }
    
    int get(int index) {
        if (index < 0 || index >= size) {
            return -1;
        }
        ListNode* p = head;
        for (int i = 0; i <= index; ++i) {
            p = p->next;
        }
        return p->val;
    }
    
    void addAtHead(int val) {
        ListNode* node = new ListNode(val);
        node->next = head->next;
        head->next = node;
        ++size;
    }
    
    void addAtTail(int val) {
        tail->next = new ListNode();
        tail->val = val;
        tail = tail->next;
        ++size;
    }
    
    void addAtIndex(int index, int val) {
        if (index > size) {
            return;
        }
        // 找到index前一个节点
        ListNode* pre = head;
        for (int i = 0; i < index; ++i) {
            pre = pre->next;
        }
        // 插入新节点
        ListNode* node = new ListNode(val);
        node->next = pre->next;
        pre->next = node;
        ++size;
    }
    
    void deleteAtIndex(int index) {
        if (index < 0 || index >= size) {
            return;
        }
        ListNode* pre = head;
        for (int i = 0; i < index; ++i) {
            pre = pre->next;
        }
        ListNode* node = pre->next;
        pre->next = node->next;
        delete node;
        --size;
    }

private:
    int size;
    ListNode* head;
    ListNode* tail;
};

9.设计推特

哈希表+链表+优先队列

class Twitter {
public:
    Twitter() {
        curTime = 0;
        maxTweet = 10;
    }
    
    // 根据给定的 tweetId 和 userId 创建一条新推文
    void postTweet(int userId, int tweetId) {
        checkUser(userId);
        TweetNode* t = new TweetNode(tweetId, curTime++);
        t->next = userMap[userId]->tweets->next;
        userMap[userId]->tweets->next = t;
    }
    
    // 检索当前用户新闻推送中最近10条推文的ID，按时间由近到远 (必须是自己和关注人的)
    vector<int> getNewsFeed(int userId) {
        checkUser(userId);
        // 将userId自己以及所有关注的人的推特合并——使用优先队列（最小堆）
        priority_queue<TweetNode*, vector<TweetNode*>, decltype(&cmp)> heap(cmp);
        // 自己的博文放入堆中
        TweetNode* t = userMap[userId]->tweets->next;
        while (t) {
            heap.push(t);
            t = t->next;
        }
        // 关注的人的博文放入堆中
        for (auto id : userMap[userId]->followIds) {
            t = userMap[id]->tweets->next;
            while (t) {
                heap.push(t);
                t = t->next;
            }
        }
        // 取堆中前maxTweet条博文
        vector<int> res;
        int len = min(static_cast<int>(heap.size()), maxTweet);
        for (unsigned int i = 0; i < len; ++i) {
            res.push_back(heap.top()->tweetId);
            heap.pop();
        }
        return res;
    }
    
    // userId1 的用户开始关注ID为 userId2 的用户
    void follow(int userId1, int userId2) {
        checkUser(userId1);
        checkUser(userId2);
        userMap[userId1]->followIds.insert(userId2);
    }
    
    // userId1 的用户取消关注ID为 userId2 的用户
    void unfollow(int userId1, int userId2) {
        checkUser(userId1);
        checkUser(userId2);
        userMap[userId1]->followIds.erase(userId2);
    }

protected:
    struct TweetNode {
        int tweetId;
        int time;    // 发推时间
        TweetNode* next;
        TweetNode() : tweetId(-1), time(-1), next(nullptr) {}
        TweetNode(int t1, int t2) : tweetId(t1), time(t2), next(nullptr) {}
    };

    struct User {
        int userId;
        unordered_set<int> followIds; // 该用户关注的人
        TweetNode* tweets;            // 该用户发的推特
        User() : userId(-1) {
            tweets = new TweetNode();
        }

        User(int userId_) : userId(userId_) {
            tweets = new TweetNode();
        }
    };

    // 新推文排在前面
    static bool cmp(TweetNode* a, TweetNode*b) {
        return a->time < b->time;
    }

    // 当用户不存在时创建用户
    void checkUser(int userId) {
        if (userMap[userId] == nullptr) {
            userMap[userId] = new User(userId);
        }
    }

private:
    int curTime;  // 记录当前时间，值越大，推文越新
    int maxTweet; // 最多推送的推特个数
    unordered_map<int, User*> userMap; // 存储用户Id->用户信息
};

其它

1.链表组件

哈希表存储数组提高查找效率。

class Solution {
public:
    int numComponents(ListNode* head, vector<int>& nums) {
        unordered_set<int> st(nums.begin(), nums.end());
        int exits = 0;
        int res = 0;
        while (head) {
            if (st.count(head->val)) {
                exits = 1;
            } else {
                res += exits;
                exits = 0;
            }
            head = head->next;
        }
        return exits ? res + 1 : res;
    }
};

[2.找出临界点之间的最小和最大距离]

class Solution {
public:
    vector<int> nodesBetweenCriticalPoints(ListNode* head) {
        if (!head || !head->next || !head->next->next) {
            return {-1, -1};
        }

        int minn = INT_MAX;
        int maxn = 0;
        int lastPos = -1;
        int pos = 2;
        int cnt = 0;
        while (head->next->next) {
            ListNode* curr = head->next;
            ListNode* next = curr->next;
            if ((curr->val > head->val && curr->val > next->val) || (curr->val < head->val && curr->val < next->val)) {
                minn = min(minn, lastPos == -1 ? INT_MAX : pos - lastPos);
                maxn += lastPos == -1 ? 0 : (pos - lastPos);
                lastPos = pos;
                ++cnt;
            } 
            head = head->next;
            ++pos;
        }
        if (cnt < 2) {
            return {-1, -1};
        }
        return {minn, maxn};
    }
};