《动手学深度学习》-67自注意力

news2024/10/1 1:30:40

沐神版《动手学深度学习》学习笔记，记录学习过程，详细的内容请大家购买书籍查阅。
b站视频链接
开源教程链接

自注意力

在深度学习中，经常使用卷积神经网络（CNN）或循环神经网络（RNN）对序列进行编码。有了注意力机制之后，我们将词元序列输入注意力汇聚中，以便同一组次元同时充当查询、键和值。由于查询、键和值来自于同一组输入，因此被称为自注意力(self-attention)。

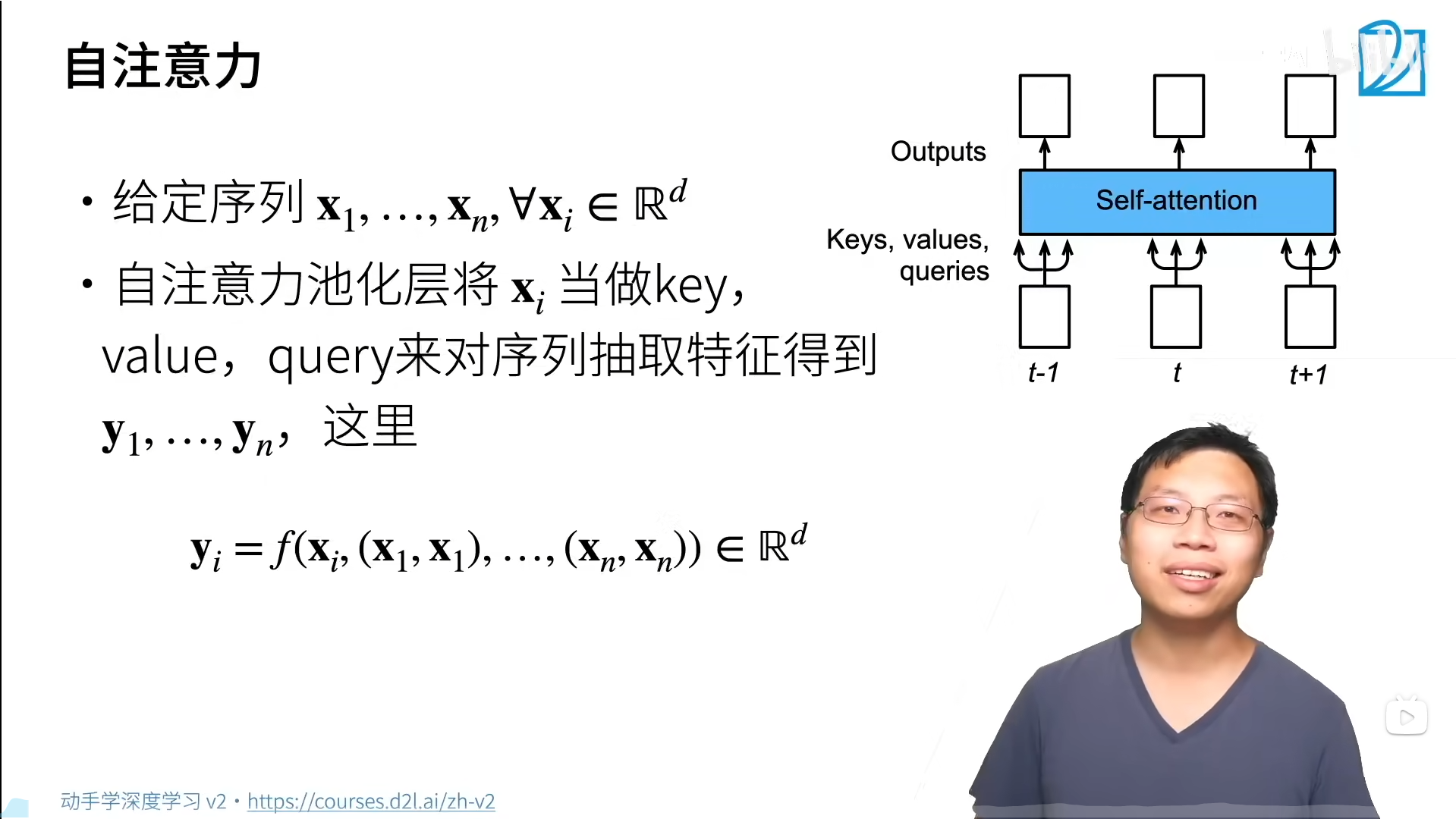
在这里插入图片描述

给定一个由词元组成的输入序列 $x 1, ..., x n$ ，该序列的自注意力输出为一个长度相同的序列 $y 1, ..., y n$ 。

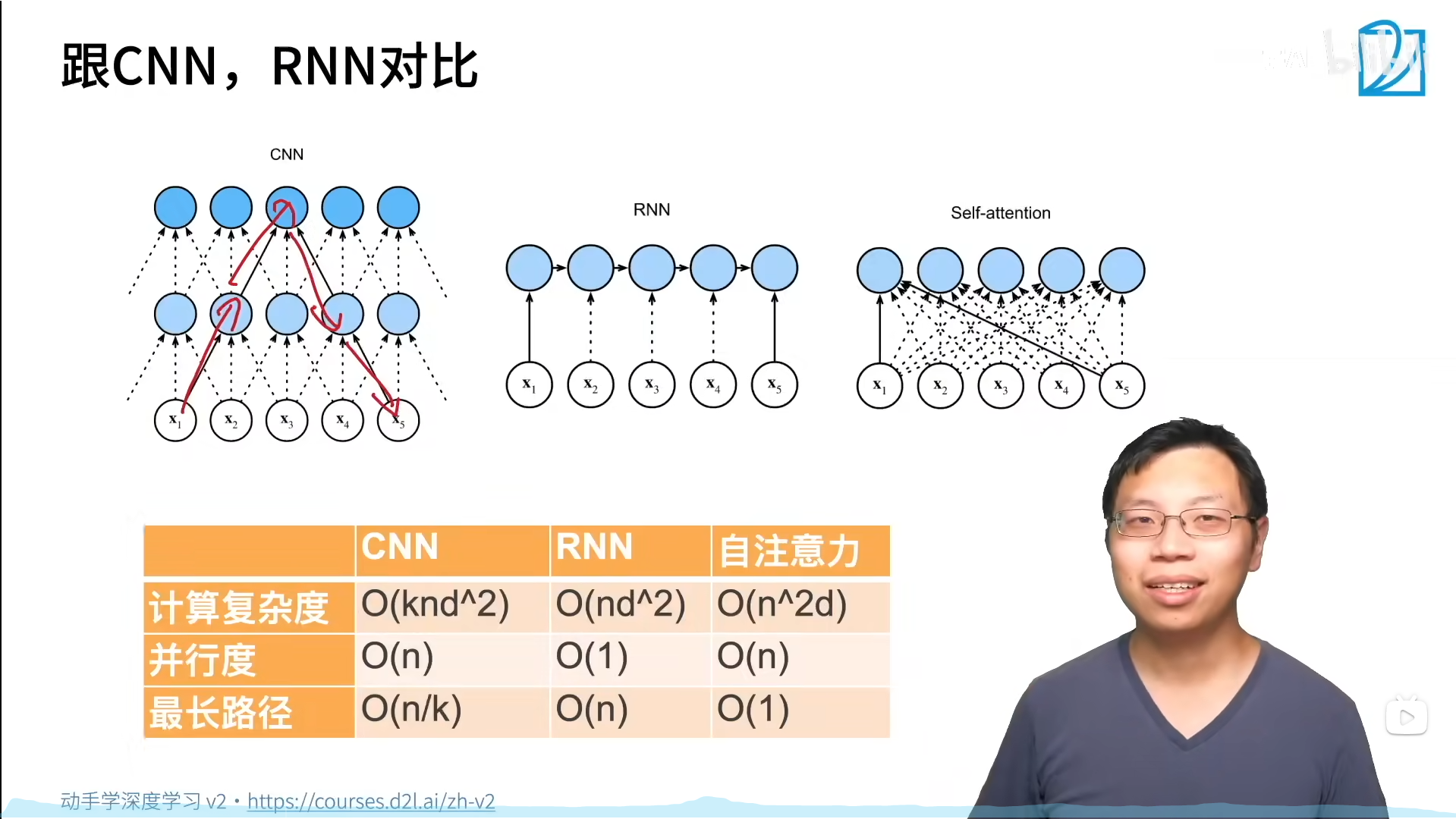
在这里插入图片描述

比较卷积神经网络、循环神经网络和自注意力

比较三种架构的计算复杂度、顺序操作和最大路径长度，三种架构都是将由 $n$ 个词元组成的序列映射到另一个长度相同的序列。

CNN的最长路径≈感受野，RNN无法并行。

在这里插入图片描述

在处理词元序列时，循环神经网络是逐个重复地处理词元的，而自注意力则是因为并行计算而放弃了顺序操作。为了使用序列的顺序信息，通过在输入表示中添加位置编码(positional encoding)来注入绝对的或相对的位置信息。位置编码可以通过学习得到，也可以直接固定。

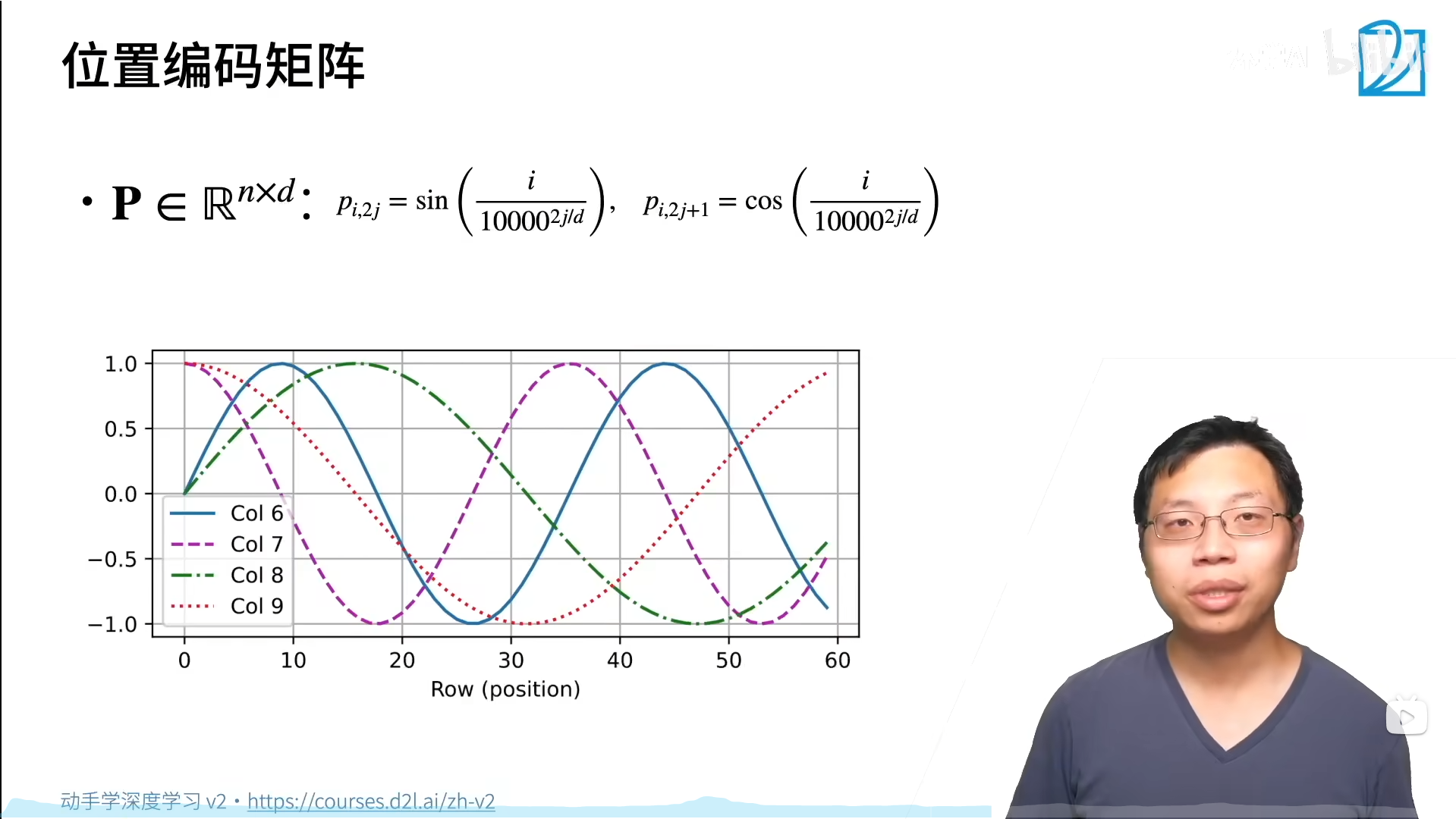
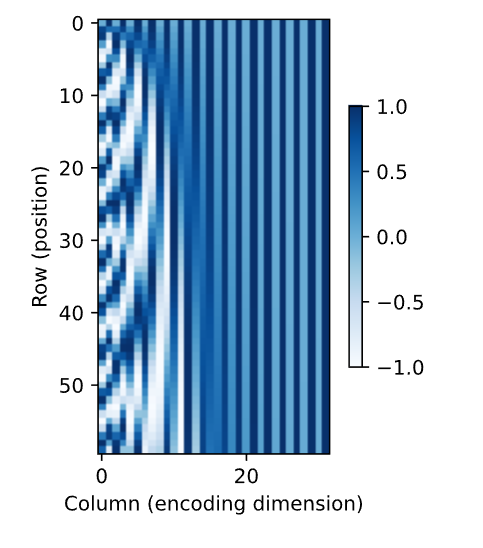
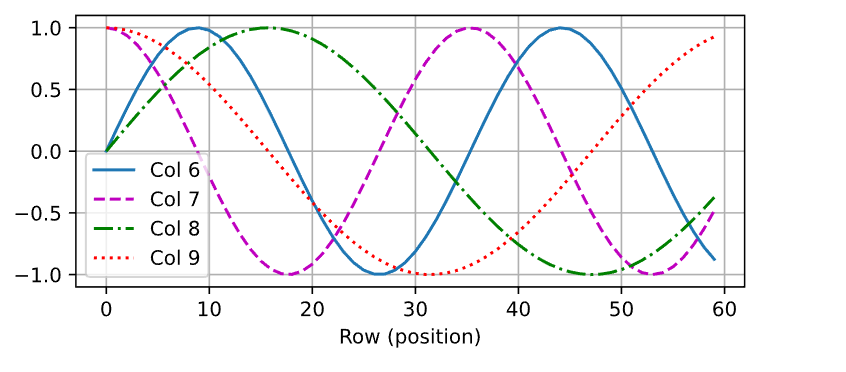
在这里插入图片描述

奇列和偶列（6和7）位移不一样（sin变cos），奇列和奇列（7和9）周期不一样。总之每个样本加的位置编码不同。加进去的好处是不改变模型，坏处是不知道模型是否能够学到。

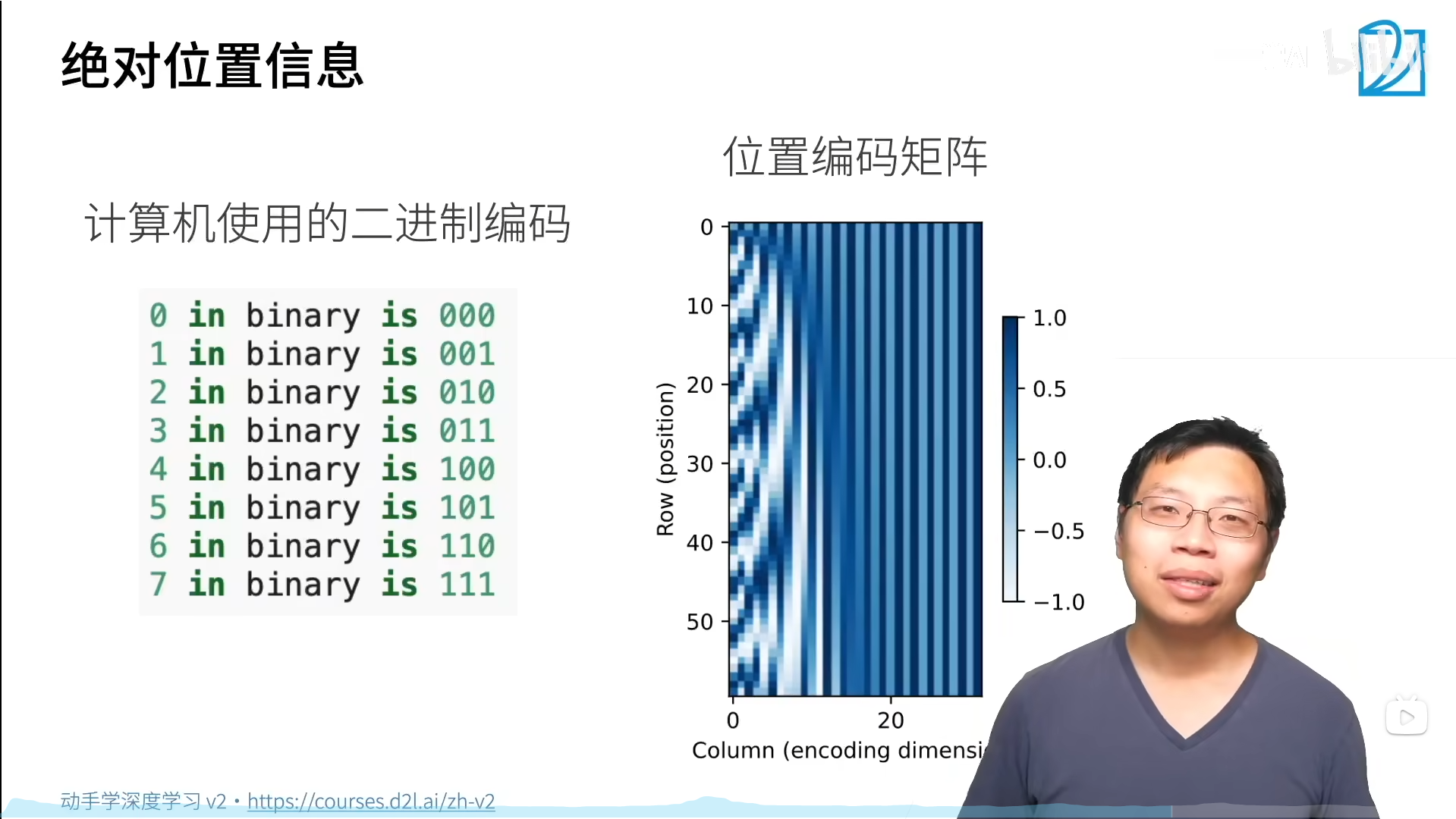
在这里插入图片描述

在二进制表示中，较高位的交替频率低于较低位，类似位置编码的热图，只是位置编码通过使用三角函数在编码维度上降低频率。由于输出是浮点数，因此此类连续表示比二进制表示更节省空间。

在这里插入图片描述

除了捕获绝对位置信息，上述位置编码还允许模型学习得到输入序列中的相对位置信息，这是因为对于任何确定的位置偏移 $\delta$ ，位置 $i+\delta$ 处的位置编码可以用线性投影位置i处的位置编码来表示。

总结
在这里插入图片描述
卷积神经网络和自注意力都具有并行计算的优势，而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的平方，所以在很长的序列中计算会非常慢。

动手学

自注意力

import torch
from torch import nn
from d2l import torch as d2l

num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
                                   num_hiddens, num_heads, 0.5)
attention.eval()

MultiHeadAttention(
  (attention): DotProductAttention(
    (dropout): Dropout(p=0.5, inplace=False)
  )
  (W_q): Linear(in_features=100, out_features=100, bias=False)
  (W_k): Linear(in_features=100, out_features=100, bias=False)
  (W_v): Linear(in_features=100, out_features=100, bias=False)
  (W_o): Linear(in_features=100, out_features=100, bias=False)
)

batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
attention(X, X, X, valid_lens).shape

torch.Size([2, 4, 100])

位置编码

#@save
class PositionalEncoding(nn.Module):
    """位置编码"""
    def __init__(self, num_hiddens, dropout, max_len=1000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(dropout)
        # 创建一个足够长的P
        self.P = torch.zeros((1, max_len, num_hiddens))
        X = torch.arange(max_len, dtype=torch.float32).reshape(
            -1, 1) / torch.pow(10000, torch.arange(
            0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
        self.P[:, :, 0::2] = torch.sin(X)
        self.P[:, :, 1::2] = torch.cos(X)

    def forward(self, X):
        X = X + self.P[:, :X.shape[1], :].to(X.device)
        return self.dropout(X)

encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
         figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])

在这里插入图片描述

P = P[0, :, :].unsqueeze(0).unsqueeze(0)
d2l.show_heatmaps(P, xlabel='Column (encoding dimension)',
                  ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')