1.前言
在Scratch中,对于坐标系上的两点,我们可以确定通过x坐标或y坐标之差确定两点横坐标或是纵坐标上的距离,那么如何知道两点之间的直线距离呢?
2.勾股定理
对于一个直角三角形,两条直角边的平方和等于斜边的平方,勾股定理 :a^2+b^2=c^2
勾股定理将作为确定两点之间距离算法的核心原理,下文参考百度百科:
勾股定理,是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以称这个定理为勾股定理,也有人称商高定理。
勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一。勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
在中国,周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例。在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他们用演绎法证明了直角三角形斜边平方等于两直角边平方之和。
3.基本算法
对于前言中的问题,我们不妨在两点之间构造一个直角三角形,以两点之间的直线距离为斜边,如图
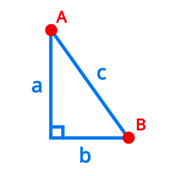
通过勾股定理我们可以知道,两点之间的距离c可以通过以下表达式得到:
![]()
因此,只需知道a,b的值,我们就可以知道A,B之间的距离,通过sc中的坐标系,我们不难得到:

简单进行解释,由于平方带有非负性,所以绝对值可以去掉
a, b的值分别为A,B两点x坐标和y坐标上的差值
4.代入Scratch
在Scratch中,我们可以专门写一个函数用于测量两点之间的距离,通过上面的推理可知,我们的参数只需要这两个点各自的x,y坐标

勾选运行时不刷新屏幕,立刻完成距离测算
x0, y0 为A点坐标,x1, y1 为B点坐标,代入表达式,具体如下:

这样一来,两点之间的距离就被存储在了 #distance 私有变量中
5.结束语
该算法可适用范围极大,比如检测克隆体间的碰撞,不能用侦测积木,就可通过测算两点之间距离来判定是否接触。
以上就是关于两点之间距离测算的全部内容,喜欢的话请多多支持作者。