Softmax原理

---

Softmax函数用于将分类结果归一化，形成一个概率分布。作用类似于二分类中的Sigmoid函数。

对于一个k维向量z，我们想把这个结果转换为一个k个类别的概率分布p(z)。softmax可以用于实现上述结果，具体计算公式为：

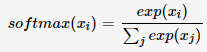
对于k维向量z来说，其中zi∈Rzi∈R，我们使用指数函数变换可以将元素的取值范围变换到(0,+∞)(0,+∞),之后我们再所有元素求和将结果缩放到[0,1],形成概率分布。

常见的其他归一化方法，如max-min、z-score方法并不能保证各个元素为正，且和为1。

Softmax性质

---

输入向量x加上一个常数c后求softmax结算结果不变，即:

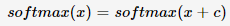
我们使用softmax(x)的第i个元素的计算来进行证明：

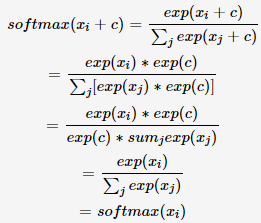
函数实现

---

由于指数函数的放大作用过于明显，如果直接使用softmax计算公式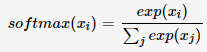进行函数实现，容易导致数据溢出(上溢)。所以我们在函数实现时利用其性质：先对输入数据进行处理，之后再利用计算公式计算。具体使得实现步骤为：

1. 查找每个向量x的最大值c；
2. 每个向量减去其最大值c, 得到向量y = x-c;
3. 利用公式进行计算$softmax(x)=softmax(x-c)=softmax(y)$

import numpy as np
def softmax(x, axim=1):
    '''
    x: m*n m个样本，n个分类输出
    return s：m*n
    '''
    row_max = np.max(x, axis=axis) # 计算最大值
    row_max = row_max.reshape(-1, 1) # 将数据展开为m*1的形状，方便使用广播进行作差
    x = x - row_max # 减去最大值
    x_exp = np.exp(x) # 求exp
    s = x_exp / np.sum(x_exp, axis=axis, keepdim=True) # 求softmax
    return s