一.二叉树的最近公共祖先

链接

二叉树的最近公共祖先

题目再现

 『Ⅰ』思路一：转换成相交链表问题

 观察上图，节点1和节点4的最近公共祖先是3，这是不是很像相交链表的问题，关于相交链表，曾经我在另一篇文章里写到过，读者可以参考：反转链表 合并链表 相交链表

但是要转换成相交链表，就要从后向前遍历，如果节点中还存在一个指针，指向父节点就好了，这种结构其实叫三叉链结构：

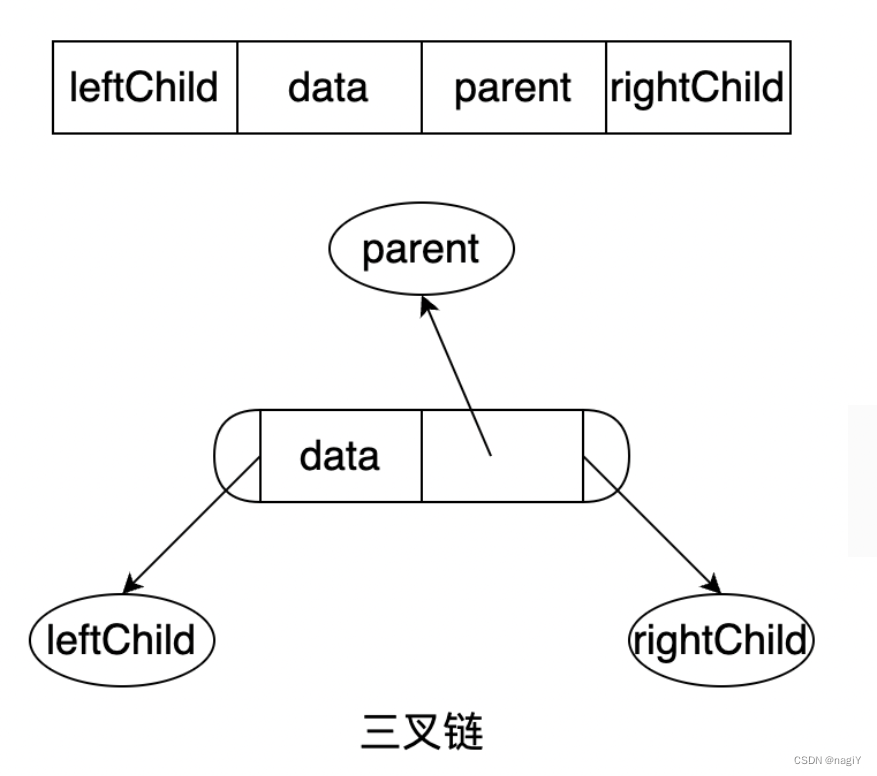
 但是这题给我们的只是一个普通的二叉树，没有三叉链，那该怎么办呢？

那么就转换为第二种思路：寻找节点的祖先路径

『Ⅱ』思路二：寻找节点的祖先路径

  我们可以把要找的两个节点的路径找出来，然后存到栈里，这样把两个节点的祖先路径找出来后，就可以转换成链表相交问题了。

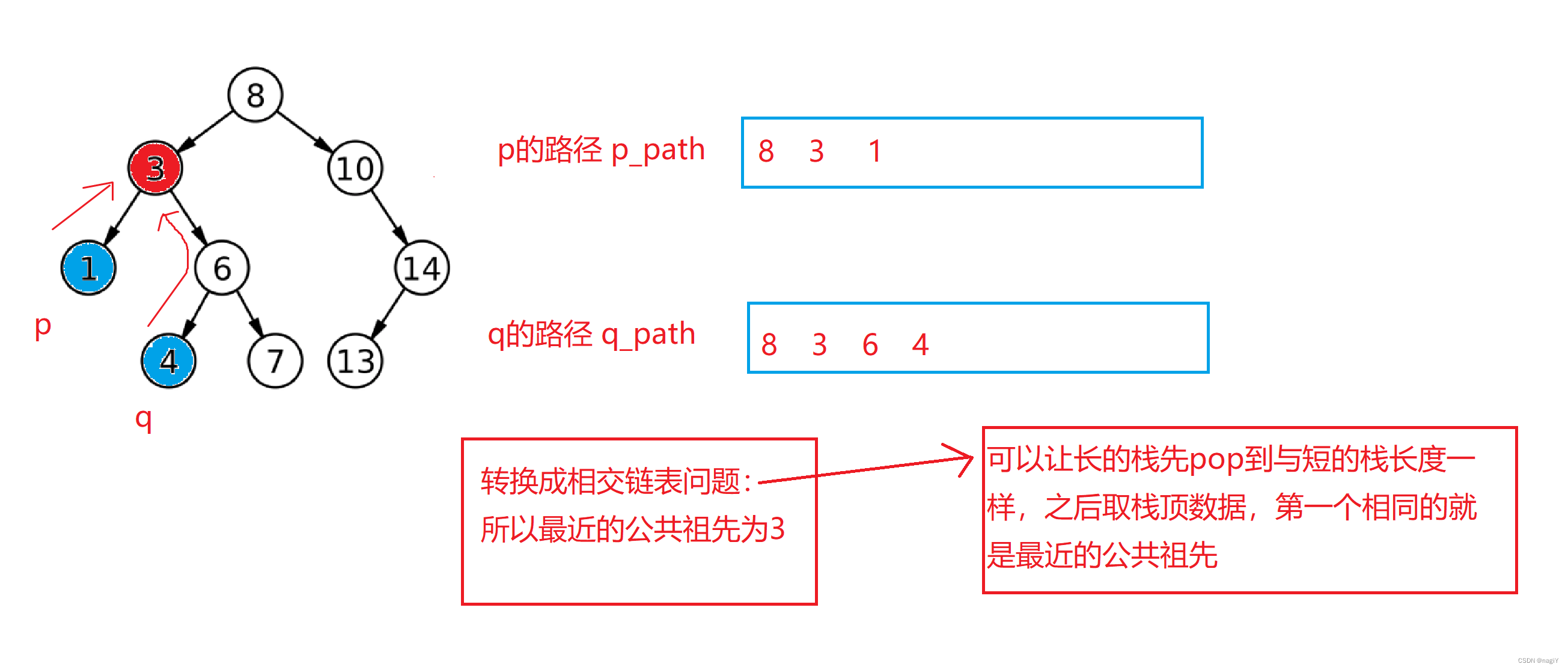
关于该怎么入栈：

我们先让节点入栈，然后判断它是否等于我们要找的节点，如果是，则返回true；如果不是，则

                1.如果左节点不为空，返回true；

                2.如果右节点不为空，返回true；

                3.如果左右节点都为空，则pop掉栈顶的元素，返回false；

完整代码：

class Solution {
public:
    bool findpath(TreeNode*cur,TreeNode*x,stack<TreeNode*>&path)  //注意这里要传引用
    {
        if(cur==nullptr)
            return false;
        path.push(cur);
        if(cur==x)
            return true;
    
        if(findpath(cur->left,x,path))
            return true;
        if(findpath(cur->right,x,path))
            return true;

        path.pop();
        return false;
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) 
    {
        stack<TreeNode*> ppath;
        stack<TreeNode*> qpath;
        findpath(root,p,ppath);
        findpath(root,q,qpath);
        while(ppath.size()>qpath.size())  //使两个栈一样长
        {
            ppath.pop();
        }

        while(ppath.size()<qpath.size())
        {
            qpath.pop();
        }

        while(ppath.top()!=qpath.top())   //从栈顶开始，寻找第一个相同的数据
        {
            ppath.pop();
            qpath.pop();
        }

        return ppath.top();
    }
};

         

可以看到，这种方法效率使非常高的，它的时间复杂度是O（N）;

 『Ⅲ』思路三：暴力查找

其实当两个节点分别在左树和右树时，它们最近的公共祖先就是根节点，如果不在树两边，而是都在左树，或是都在右树，那么就可以转化成子问题，递归解决。

如下图：

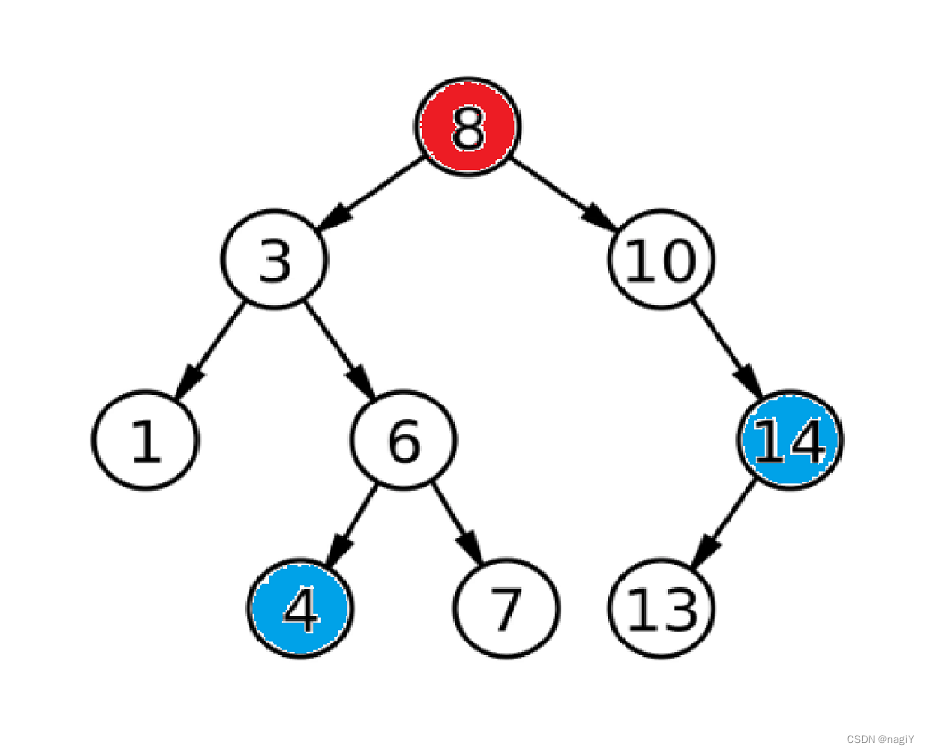
 注意，如果有一个节点恰好是根节点，那么这个节点就是最近的公共祖先，也是说一个节点的祖先也算它自己。

如下图：

 那么该怎么判断节点是在左树还是右树呢?

我们可以定义四个布尔变量，分别是：pinleft（p在左树）   pinright（p在右树）

                                                             qinleft （q在左树 ） qinright（q在右树）

哪个布尔值为真就表明这个节点在哪边。

完整代码：

class Solution {
public:
    bool find(TreeNode*cur,TreeNode*x)
    {
        if(cur==nullptr)
            return false;
        return cur==x||
               find(cur->left,x)||
               find(cur->right,x);
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode*q)  
    {
        if(root==nullptr)
            return nullptr;
        if(root==p||root==q)  //某一个节点为根
            return root;
        
        bool pinleft,pinright;
        bool qinleft,qinright;
        pinleft=find(root->left,p);   //去左树寻找p节点
        pinright=!pinleft;
        qinleft=find(root->left,q);   //去左树寻找q节点
        qinright=!qinleft;
        if(pinleft&&qinleft)   //都在左树转化成子问题
            return lowestCommonAncestor(root->left,p,q);
        else if(pinright&&qinright)    //都在右树转化成子问题
            return lowestCommonAncestor(root->right,p,q);
        else    //分别在左树和右树
            return root;
    }
};

可以看到，这个算法的效率是很差的，它的时间复杂度是O（N^2）。

---

二.二叉搜索树转换成排好序的双向链表 

链接

二叉搜索树转换成排好序的双向链表

题目再现

 解法

根据题意，原二叉搜索树的左指针就是双链表的前驱指针，右指针就是双链表的后继指针；

而且本题还要求空间复杂度是O（1），也就是说不能额外开空间，其实要是能额外开空间，那么这题就非常简单了。

我们知道，二叉搜索树的中序遍历结果是升序列，这恰好满足了题目排好序的要求；

那要怎么在原树上操作，使它转换成双链表呢？

举个例子：

对于我们过去（prev）的事，现在（cur）的我们肯定是一清二楚的，而且是可以确定的，但未来（next）的事并不能确定；

但如果我们是从未来穿越回现在的，那么穿越回来的我们，就可以确定未来的事。所以说过去（prev）的未来（next）就是现在（cur）。

回到题目，所以cur的左指针（left）就是双链表的前驱（prev），prev的右指针就是后继（next），然后再更新一下prev即可。

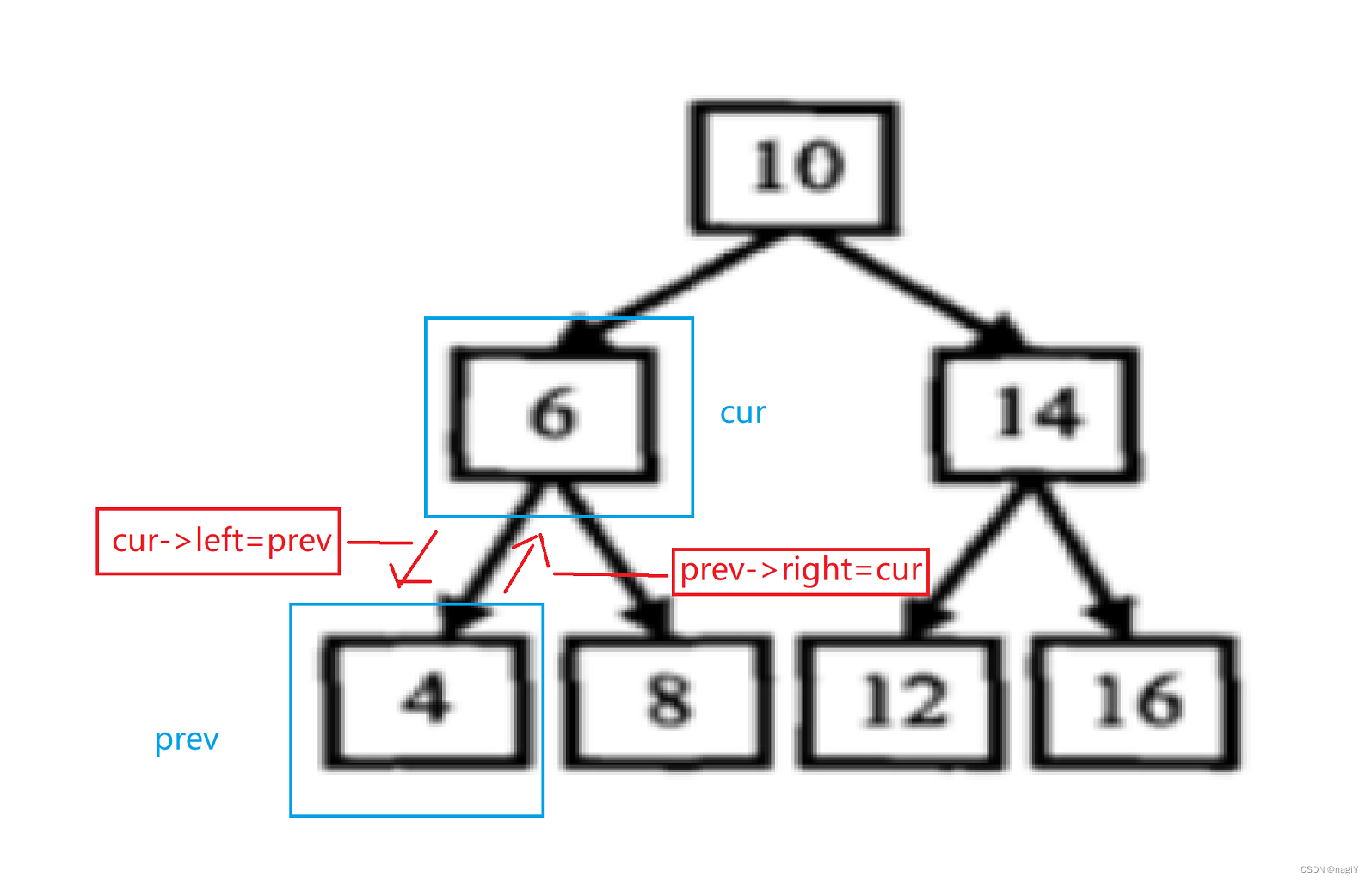
完整代码：

class Solution {
public:
	void InOrder(TreeNode*cur,TreeNode*&prev)   //注意要传引用
	{
		if(cur==nullptr)
			return;
		
		InOrder(cur->left,prev);
		cur->left=prev;   //cur的左指针就是prev
		if(prev)   //注意判断prev是否为空
			prev->right=cur;   //prev的右指针就是cur
		prev=cur;  //更新prev
		InOrder(cur->right,prev);
	}
    TreeNode* Convert(TreeNode* pRootOfTree) 
	{
		if(pRootOfTree==nullptr)
			return nullptr;
		TreeNode*prev=nullptr;   //定义一个前驱指针
		InOrder(pRootOfTree,prev);   //中序遍历
		TreeNode*head=pRootOfTree;
		while(head->left)   //最左边的节点即为双链表的头
		{
			head=head->left;
		}

		return head;
    }
};

---

三.根据一棵树的前序遍历与中序遍历构造二叉树

链接

根据一棵树的前序序列与中序序列构建二叉树

题目再现

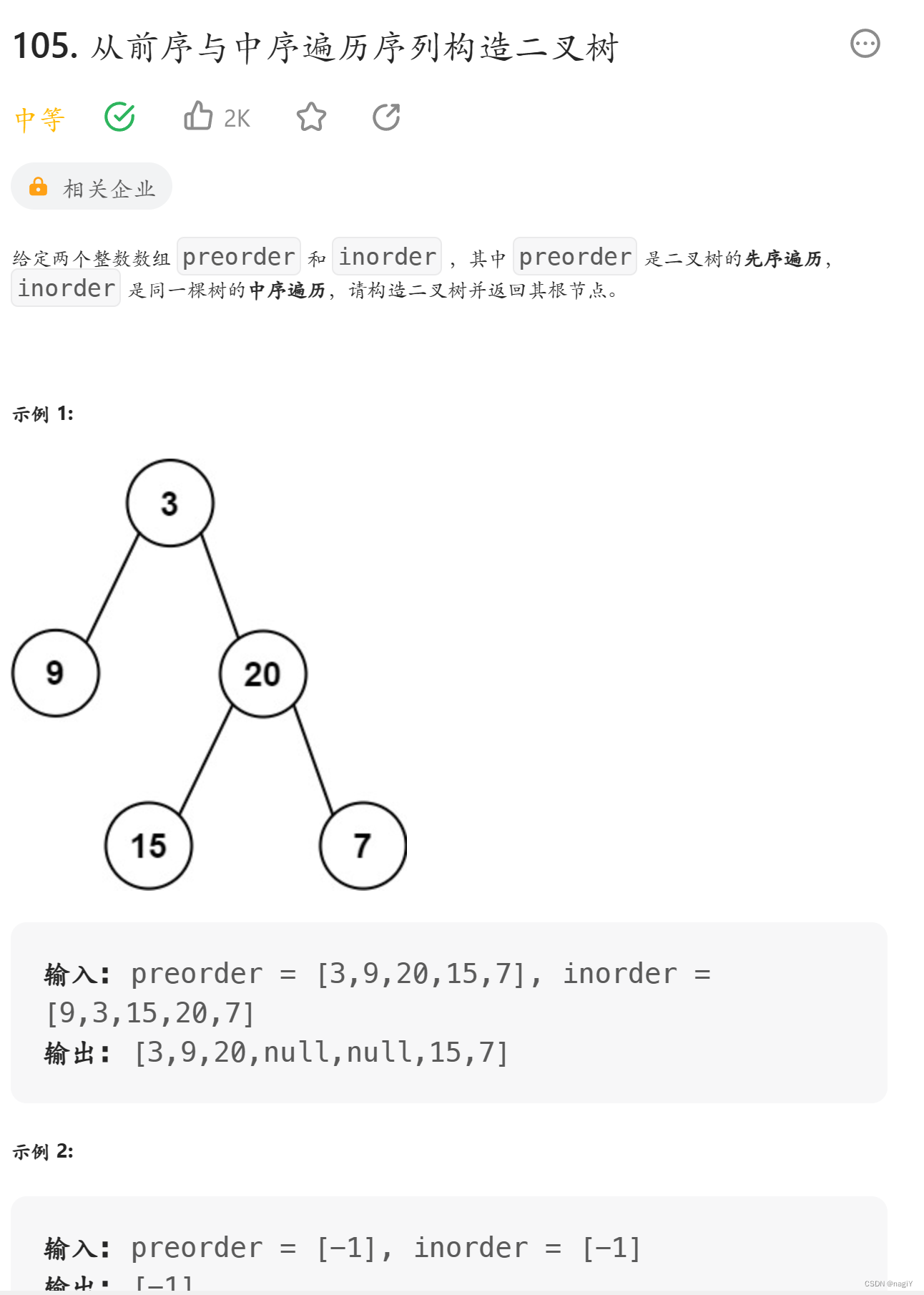
 解法

众所周知，前序遍历的顺序为：根  左  右

                  中序遍历的顺序为：左  根  右

所以根据前序序列就可以确定根，确定了根后就可以分成左子树和右子树；

确定好根后，根据中序序列就可以分割左子树和右子树的区间，然后构建树；

而左子树或是右子树也有根，这样就可以转化成子问题，递归实现，但要注意，前序序列中的每个数只能使用一次。

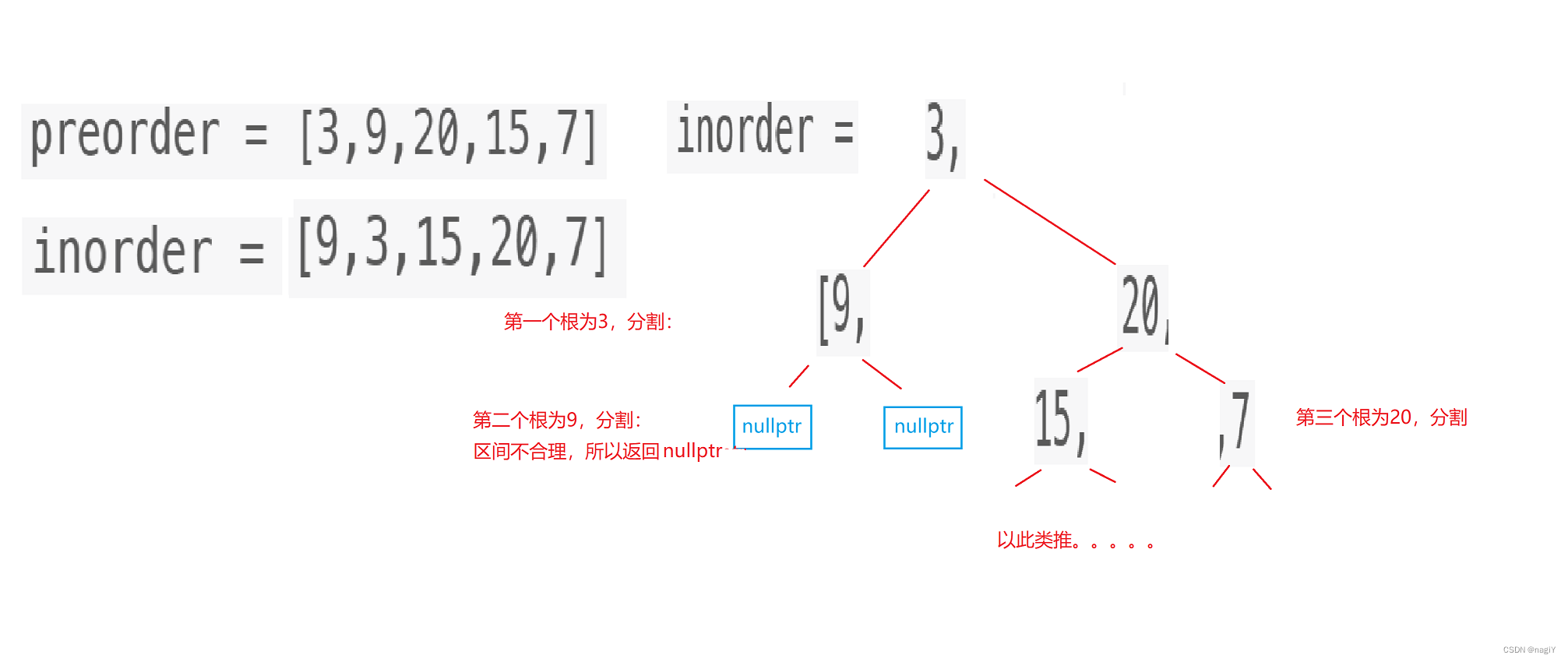
 完整代码：

class Solution {
public:
    //注意这个prei用于遍历前序序列数组，因为每个数只能用一次，所以要传引用
    TreeNode*_build(vector<int>& preorder, vector<int>& inorder,int &prei,int inbegin,int inend)
    {
        if(inbegin>inend)   //当区间不存在时返回空指针
            return nullptr;
       
        TreeNode*preroot=new TreeNode(preorder[prei]);
        int rooti=inbegin;     //找根在中序序列中的位置
        while(rooti<=inend)
        {
            if(preorder[prei]==inorder[rooti])   //找到后跳出循环
                break;
            rooti++;
        }
        prei++;   //本次确定好根后，prei++找下一个根
        //分割区间，递归构建
        //[inbegin,rooti-1] rooti [rooti+1,inend]
        preroot->left=_build(preorder,inorder,prei,inbegin,rooti-1);
        preroot->right=_build(preorder,inorder,prei,rooti+1,inend);

        return preroot;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) 
    {
        int i=0;
        return _build(preorder,inorder,i,0,inorder.size()-1);
    }
};

---

🐬🤖本篇文章到此就结束了， 若有错误或是建议的话，欢迎小伙伴们指出；🕊️👻

😄😆希望小伙伴们能支持支持博主啊，你们的支持对我很重要哦；🥰🤩

😍😁谢谢你的阅读。😸😼